Rate Stat Series, pt. 15: Mixing Frameworks

Thus far I have employed what I’ve described as a “puritanical” approach to matching run estimator, denominator, and win conversion for each of the three frameworks for evaluating an individual’s offensive performance. While I think my logic for this approach is sound, I do not think it is necessarily wrong to mix components in a different manner than I’ve described. This will be a brief discussion of which of these potential hybrids make more sense than others, and a few issues to keep in mind if you choose to do so.

For the player as a team framework, there are many places in the process in which a batter’s value (at least to the extent that we can define and model it) as a member of a real team is distorted. At the very beginning of the process, a dynamic run estimator is applied directly to individual statistics. This creates distortion. Then the rate stat is runs/out; this doesn’t create a tremendous amount of distortion, as runs/out is a defensible if not perfect choice for an individual rate stat even if you don’t use the player as a team framework. Then if we convert to win value, we create a tremendous amount of distortion by essentially multiplying the run distortion by nine – instead of just mis-estimating an individual’s run contribution, we compound the problem by assuming that the entire team hitting like him would shape the run environment to be something radically different from the league average.

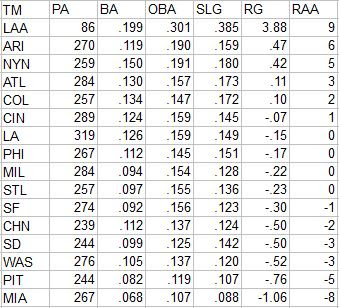
This is an opportune juncture to make a point that I should have made earlier in the series – for league average hitters, the distortion will be very small, and the differences across all of the various methodologies we’ve discussed will be lesser. I have focused in this series on a small group of hitters, basically the five most productive and five least productive in each league-season. These are of course the hitters most impacted by different methodological decisions. A league average hitter would by definition have Base Runs = LW_RC = TT_BsR (at least as we’ve linked these formulas in this series), would by definition have 0 RAA or 0 WAA, would by definition have a 100 relative rate, regardless of which approach you take. This series, and more generally my sabermetric interests, tend to focus on the extreme cases, and evaluating methods with an eye to applicability to a wide range of performance levels. Additionally, extreme players are the ones people in general tend to care the most about – you can imagine people debating who had the better offensive season, Frank Robinson in 1966 or Frank Thomas in 1994. I cannot imagine many people doing the same for Earl Battey and Gary Gaetti.

While we could avoid compounding the issues in the player as a team approach, but why bother? The framework is inferior to linear weights or theoretical team in every possible way, except one could argue ease of calculation gives it an advantage over TT. The only value to be had in evaluating a player as a team is a theoretical exercise, and if you lose commitment to that theoretical exercise it ceases to have any value at all.

For the theoretical team framework, you could just calculate TT_BsR, and then treat it in the same way as linear weights, or calculate TT_BsRP and treat it in the same way as R+. However, it would be pretty silly to go through the additional effort needed to calculate the TT run estimates instead of their linear weight analogues only to use them in the same way. Unlike in the case of player as team, there is no argument to be made here that you would be making the results more reasonable by doing so, as the TT estimates can be combined with team-appropriate rate stat denominators and team-appropriate conversions from runs to wins. Here the result of mixing frameworks would be extra work coupled with less pure results.

The only mixture of frameworks that makes sense, then, is to mix the run estimation components of the linear weights framework with the rate stat and win conversion components of the theoretical team framework. A logical path that might defend this approach would be: It is questionable whether the valuation of tertiary offensive contribution claimed by theoretical team approach are accurate or material. Thus our best estimate of a player’s run contribution to a theoretical team remains his linear weights RC or RAA. When it comes to win estimation, we are on much firmer ground in understanding how team runs and runs allowed translate to wins than we are in measuring individual contributions to team runs. We shouldn’t refuse to use this knowledge in the name of methodological consistency, but rather we should use the best possible estimates for each component of the framework. That means using the full Pythagenpat approach coupled with linear weights run estimates.

Convinced? I’m not, but let me walk through an example of how we could apply this hybrid approach to the Franks. We can start with our wRC estimate, which we will now use in place of TT_BsRP as “R_+” going forward for this hybrid linear-theoretical team framework. Then we can use any of our TT rate stats  - I’ll show R+/O+ rather than R+/PA+ here, as I think it’s the former that might serve to make this hybrid framework an attractive option. R+/O+ allows us to express the individual and team rate on the same basis and better yet, doing so while using the most fundamental of rate stats (R/O) as that basis.

O+ remains equal to PA*(1 – LgOBA), and these relative R+/O+ figures are the same as our relative R+/PA, which makes sense – the numerators are the same, and the only difference in the denominators is multiplying PA by (1 – LgOBA). So an alternative way of expressing the relationship is:

R+/O+ = (R+/PA)/(1 – LgOBA)

I will skip some steps here, since they were all covered in the last installment – no need to convert this to a W% and then convert back to a relative adjusted R+/O+.  

TT_R/O = (R+/O+)*(1/9) + LgR/O*(8/9)

TT_x= ((TT_R/O)*LgO/G + LgR/G)^.29

TT_WR = ((TT_R/O)/Lg(R/O))^TT_x

RelAdj R+/O+ = (TT_WR^(1/r) - 1)*9 + 1

It might be helpful to take a step back and look at our results for the relative adjusted metric (whether R+/PA or R+/O+) for each of the four options we’ve considered, which are:

A: linear run estimate and fixed RPG based on league average (final rate based on R+/PA)

B: linear run estimate and dynamic RPG based on player’s impact on team (final rate based on R+/PA)

C: linear run estimate and Pythagenpat theoretical team win estimate (hybrid approach discussed in this installment; final rate based on R+/O+)

D: theoretical team run estimate (full theoretical team approach; final rate based on R+/O+)

I included a third row which shows the percentage by which Thomas’ figure exceeded Robinson’s. The TT (D) approach maximizes each player’s value and also the difference between them. The hybrid approach (C) falls in between the pure linear approach (A) and the TT approach (D). One thing that I did not fully expect to see is that the linear approach that varies RPW based on the estimated RPG of a team with the player added (B) produces a lower estimate than any of the other approaches, and is the outlier of the bunch. I didn’t make enough of this in part 13, but we are actually better off assuming that the individual has no impact on RPW than adjusting RPW based on his own impact on the theoretical team’s RPG.

Note that when we translate to a reference league, we are fixing each theoretical team's RPG to the same level. In reality, the Frank Thomas TT will have a higher RPG than the Matt Walbeck TT for any given reference environment. However, this is not an issue, because the runs value we're reporting is not real. It is intended to be an equivalent run value that reflects the player's win contribution for a common frame of reference. When we use the full Pythagenpat approach, the theoretical team's winning percentage is preserved, so the runs are now an abstract quantity and do not need to tie out to any actual number of runs in this environment. In this sense, when we convert TT to a win-equivalent rate, we're doing something similar to what I said the linear weights framework was doing - we're making the run environments equal after adding the player. The difference is that in this case we are capturing the disparate impact of the players on team wins first, then restating a win ratio as an equivalent run ratio given the assumption of a stable run environment. Thus the runs are an abstraction, but the value they represent is preserved.

When we do the same with a dynamic RPW approach (i.e. when we use the Palmerian approach of adding the batter's RAA/G to the RPG and then calculating RPW), we run into difficulties because while we have fixed a WAA total, and can then translate that WAA to an equivalent for the reference environment, we have not taken into account that the batter would need to contribute more runs to actually produce the same number of wins. This is not a problem for the full Pythagenpat approach because we used a run ratio that modified the batter's abstract runs in concert with the run environment. 

Now there is a way we could address this, but it results in a mess of an equation that I'm not sure has an algebraic solution (whether it does or not, I have no interest in trying to solve it). Basically, we can solve for the RAA that would be needed to preserve the batter's original WAA in the reference environment. To do this, we need to remember to apply the reference PA adjustment. For this application, I think it’s easiest to apply directly to the batter’s original WAA, so WAA*Ref(PA/G)/Lg(PA/G):

We could then say that adjWAA = X/(2*(refRPG + X/G)^.71) where X = the batter's RAA and G could be the batter's actual game or some kind of PA-equivalent games as long as we’re consistent with what was used in the original WAA calculation. I used the Goal Seek function in Excel to solve the following equations for the Franks:

for Robinson: 8.552 = X/(2*(8.83 + X/155)^.71), X = 85.555

for Thomas: 7.217 = X/(2*(8.83 + X/113)^.71), X = 71.176

With these new estimates of RAA, we can get relative adjusted R+/PA by first dividing by each batter’s PA, then adding in the reference R/PA, and then dividing by the reference R/PA:

This approach allows us to more correctly calculate a win-equivalent rate stat for the linear weights framework when allowing RPW to vary based on the batter’s impact on his team’s run environment. However, given that I don't know how to solve for x algebraically, and my pre-existing philosophical issues with using this approach with the linear weights framework to begin with, I think that at this point there are two better choices:

1. If you want to maintain methodological purity, stick with the fixed RPW for the linear weights framework like I advocate

2. Use the hybrid framework, which embraces the "real" run to win conversion and actually makes this math easier

With "B" out of the picture, what we see for A, C, and D make sense in relation to each other. C produces a lower final relativity for great hitters like the Franks because it recognizes that when they inflate their team's run environments, RPW increases. D is higher than both because the initial run estimate is higher, due to using TT_BsR rather than LW, and thus giving each batter credit for their estimated tertiary contributions. And our revised linear weight approach falls somewhere in between.

Of course, it’s possible that I’m wrong about this, and the hybrid or theoretical team approaches that make use of Pythagenpat are overstating the impact of the player on the runs to win conversion. I can’t prove that I am right about this, but I would offer two rejoinders:

1. The full Pythagenpat approach produces the same W% for the theoretical team across different environments by definition, and that is the most important number at the end of the lined if we are trying to build a win-equivalent rate stat.

2. We should expect the results from the linear and the Pythagenpat approach to be similar (which they are after making proper adjustments), as our RPW formula is consistent with Pythagenpat for .500 teams. While the relationship between the RPW formula and Pythagenpat will fray as we insert more extreme teams, the theoretical team approach doesn’t produce any extremes for even great hitters like the Franks. For example, if we use the Palmer approach, Thomas’ 77.8 RAA in 113 games takes an average 1994 AL team that scores 5.23 R/G up to 5.92 R/G, which would rank second in the league, even with the Yankees.  This is not an extreme team performance when it comes to applying the win estimation formulas. If we use Pythagenpat, such a team would be expected to have a .5623 W% using the RPW formula and a .5620 W% using Pythagenpat. So we shouldn’t expect the results to diverge too much when applying the approaches to derive win-equivalent rate stats.

And with that, we have come to the end of everything that I wanted to say about rate stats. I will close out the series with one final installment that attempts to briefly summarize my main points with limited math.

Hitting by Position, 2021

The first obvious thing to look at is the positional totals for 2021, with the data coming from Baseball-Reference. "MLB” is the overall total for MLB, which is not the same as the sum of all the positions here, as pinch-hitters and runners are not included in those. “POS” is the MLB totals minus the pitcher totals, yielding the composite performance by non-pitchers. “PADJ” is the position adjustment, which is the position RG divided by the total for all positions, including pitchers (but excluding pinch hitters). “LPADJ” is the long-term offensive positional adjustment, based on 2010-2019 data (see more below). The rows “79” and “3D” are the combined corner outfield and 1B/DH totals, respectively:

Having reviewed this data annually for about fifteen seasons, I would strongly caution about drawing any conclusions about shifting norms from single season results, which are better treated as curiosities (and as strong warnings against using single-year or other short time period averages in developing any kind of positional adjustment for use in a player value system). The most interesting curiosity then is shortstops outhitting left fielders, essentially even with third basemen and even DHs. The bumper crop of free agent shortstops has accentuated recognition of the current strength of the position, and their collective 2021 offensive performance lives up to the hype.

However, I think the most interesting group is the pitchers. The lowest PADJ ever recorded by pitchers was -5 in 2018; they rebounded to 0 in 2019 and now fell back to -4 after taking a year off. This on its face should not be surprising, but remember that pitcher performance was buoyed by Shohei Ohtani. What would it look like sans Ohtani?

While Ohtani had only 65 PA as a pitcher (1.48% of all pitcher PA), he accounted for 6% of their doubles, 5% of their runs, RBI, and walks, and 17% of their home runs). Ohtani’s hitting as a pitcher paled in comparison to what he did as a DH, although he still created runs at 13% better rate than the MLB non-pitcher positional average. Without Ohtani, pitchers would have set a new low with a -6 PADJ. It’s interesting to consider that if the DH is made universal in the new CBA, future seasons’ data will likely show pitchers combine for competent offensive performances.

My next table is usually total pitcher performance for NL teams, but such a display would be incomplete without including the Angels. All team figures from this point forward in the post are park-adjusted. The RAA figures for each position are baselined against the overall major league average RG for the position, except for left field and right field which are pooled:

The teams with the highest RAA by position were:

C--SF, 1B--SF, 2B--LA, 3B--ATL, SS--SD, LF--CIN, CF--BAL, RF--PHI, DH--LAA

Those are pretty self-explanatory although it’s fun that Shohei Ohtani is essentially responsible for two of his teams positions ranking #1--let’s see Boster Posey or Brandon Belt do that!

I find it more entertaining to gawk at the teams that had the lowest RAA at each position (the listed player is the one who started the most games at the position, which does not always mean they were most responsible for the dreadful performance):

Hunter Dozier pulled the reverse Ohtani as the leading starter at third and right; he hit .213/.286/.390 with 3.7 RG, so it wasn’t really his fault. It’s kind of sad to see Miguel Cabrera leading the Tigers DHs to oblivion, and it kind of was his fault. Cabrera’s overall line (.256/.321/.386 for 4.2 RG) wasn’t that bad, but in 180 PA as a first baseman he posted a 844 (unadjusted) OPS while in 335 PA his OPS was just 617. 

The next table shows the correlation (r) between each team’s RG for each position (excluding pitchers) and the long-term position adjustment (using pooled 1B/DH and LF/RF). A high correlation indicates that a team’s offense tended to come from positions that you would expect it to:

I didn’t dig through years of these posts to check, but Kansas City’s negative correlation may be the lowest I’ve ever seen. The Royals only above average positions were catcher, second base, and shortstop.

The following tables, broken out by division, display RAA for each position, with teams sorted by the sum of positional RAA. Positions with negative RAA are in red, and positions that are +/-20 RAA are bolded:

A few notes:

* Only five of the fifteen AL teams had positive RAA from their position players, while each NL division had three teams with positive RAA.

* Baltimore’s infield production was the worst in the majors at -91 runs, and only Cedric Mullins’ center field prevented them from having below average performance at all positions. Texas was saved from the same fate only by their right fielders who were just +1 run; the Rangers poor production is impressive for how consistently bad it was across the board.

* Their Texas neighbors were the opposite in displaying consistently good production across the board; Houston’s outfield was the best in the majors at +63 runs, while their infield was second in the AL to Toronto. 

* San Francisco and Los Angles were nearly mirror images of each other; the Dodgers narrowly edged the Giants for the top infield in MLB (+89 to +87), while their outfielders were both slightly above average (+5 to +4). LA catchers were outstanding (their 25 RAA tied for second in the majors with the Blue Jays and ChiSox), but the Giants were better at 32 RAA, giving them a three run edge for the majors top total positional RAA.

A spreadsheet with full data is available here.

Crude Team Ratings, 2021

Crude Team Rating (CTR) is my name for a simple methodology of ranking teams based on their win ratio (or estimated win ratio) and their opponents’ win ratios. A full explanation of the methodology is here, but briefly:

1) Start with a win ratio figure for each team. It could be actual win ratio, or an estimated win ratio.

2) Figure the average win ratio of the team’s opponents.

3) Adjust for strength of schedule, resulting in a new set of ratings.

4) Begin the process again. Repeat until the ratings stabilize.

The resulting rating, CTR, is an adjusted win/loss ratio rescaled so that the majors’ arithmetic average is 100. The ratings can be used to directly estimate W% against a given opponent (without home field advantage for either side); a team with a CTR of 120 should win 60% of games against a team with a CTR of 80 (120/(120 + 80)).

First, CTR based on actual wins and losses. In the table, “aW%” is the winning percentage equivalent implied by the CTR and “SOS” is the measure of strength of schedule--the average CTR of a team’s opponents. The rank columns provide each team’s rank in CTR and SOS: 

This was not a great year for the playoff teams representing those that had the strongest W-L records in context as Toronto, Seattle, and Oakland all were significantly better than St. Louis and the world champs from Atlanta. The reason for this quickly becomes apparent when you look at the average aW%s by division (I use aW% to aggregate the performance of multiple teams rather than CTR because the latter is expressed as a win ratio—for a simple example a 90-72 team and a 72-90 team will end up with an average win ratio of 1.025 but their composite and average winning percentages will both be .500):

The NL East, despite being described by at least one feckless prognosticator as “the toughest division in baseball”, was in fact the worst division in baseball by a large margin. Atlanta had the second-weakest SOS in MLB, turning their lackluster 88-73 record into something even less impressive in context. In defense of the Braves, they did lose some significant pieces to injury and have a multi-year track record of being a strong team, as well as looking better when the CTRs are based on expected record (i.e. Pythagenpat using actual runs/runs allowed):

Here we see the Dodgers overtake the Giants by a large margin as MLB’s top team, and it actually lines up better with the playoff participants as the Braves rank highly and the Mariners drop. 

One weakness of CTR is that I use the same starting win metric to calculate both team strength and strength of schedule in one iterative process. But one could make the case that in order to best put W-L records in context, it would make more sense to use each team’s actual W-L record to determine their ranking but use expected W% or some other measure to estimate strength of schedule. Such an approach would simultaneously recognize that a team should be evaluated on the basis of their actual wins and losses (assuming the objective is to measure “championship worthiness” or some similar hard-to-define but intuitively comprehensible standard), but that just because an opponent had “good luck” or were “efficient” in converting runs to wins, they didn’t necessarily represent a stronger foe. This would give a team credit for its own “efficiency” without letting it accrue credit for its opponents “efficiency”

This is what the ratings look like using predicted W% (using runs created/runs created allowed) as the starting point:

Finally, I will close by reverting to CTRs based on actual W-L, but this time taking the playoffs into account. I am not a big fan of including the playoffs - obviously they represent additional games which provide additional information about team quality, but they are played under very different circumstances than regular season games (particular with respect to pitcher usage), and the fact that series are terminated when a team clinches biases the W-L records that emerge from series. Nonetheless, here they are, along with a column showing each team’s percentage change in CTR relative to the regular season W-L only version. Unsurprisingly, the Braves are the big winner, although they still only rank twelfth in MLB. The biggest loser are the Rays, although they still rank #3 and lead the AL. The Dodgers rating actually declined slightly more than the Giants despite winning their series;  they end up with a 6-5 record weighing down their regular season, and with seven of those games coming against teams that are ranked just #12 and #13, the uptick in SOS was not enough to offset it.

Hypothetical Award Ballots, 2021

AL ROY:

1. LF Randy Arozarena, TB

2. SP Luis Garcia, HOU

3. SP Casey Mize, DET

4. SP Shane McClanahan, TB

5. CF Adolis Garcia, TEX

Arozarena will likely win the award on name recognition if nothing else, but one could very easily make a case for Garcia, who I actually have slightly ahead in RAR 37 to 35. Arozarena’s baserunning and fielding are largely a wash, but Garcia’s RAR using eRA and dRA are slightly lower (32 and 31). That’s enough for me to slide Arozarena ahead. Adolis Garcia is an interesting case, as his standard offensive stats will probably land him high in the voting, but his OBA was only .289 which contributed to him ranking fifth among position players in RAR. But he has excellent fielding metrics (16 DRS and 12 UZR) which gets him back on my ballot. Among honorable mentions, Wander Franco had 21 RAR in just seventy games which is by far the best rate of performance. Ryan Mountcastle’s homer totals will get him on conventional ballots, but he appears to be slight minus as a fielder and was a below average hitter for a first baseman.

NL ROY:

1. 2B Jonathan India, CIN

2. SP Trevor Rogers, MIA

3. RF Dylan Carlson, STL

4. SP Ian Anderson, ATL

5. C Tyler Stephenson, CIN

India is the clear choice among position players and Rogers among pitchers, and I see no reason to make any adjustment to their RAR ordering. In fact, it’s pretty much RAR order all the way down.

AL Cy Young:

1. Robbie Ray, TOR

2. Gerrit Cole, NYA

3. Carlos Rodon, CHA

4. Jose Berrios, MIN/TOR

5. Nathan Eovaldi, BOS

The 2021 AL Cy Young race has to be the worst for a non-shortened season in history; while long-term trends are driving down starter workloads, let’s hope that a full previous season will make the 2022 Cy Young race at least a little less depressing. Robbie Ray is the obvious choice, leading the league in innings and ranking second to Carlos Rodon in RRA for a twelve-run RAR lead over Lance McCullers; Ray’s peripherals are less impressive, but are still solid. In addition to the pitchers on my ballot, McCullers, Lance Lynn, and Chris Bassitt could all easily be included as the seven pitchers behind Ray could be reasonably placed in just about any order.

NL Cy Young:

1. Zack Wheeler, PHI

2. Corbin Burnes, MIL

3. Walker Buehler, LA

4. Max Scherzer, WAS/LA

5. Brandon Woodruff, MIL

The NL race is almost the opposite of the AL, with five solid candidates who could be ranked in almost any order, even for a normal season. The easiest way to explain my reasoning is to show each pitcher’s RAR by each of the three metrics:

Wheeler and Burnes get the nods for my top two spots as they were equally good in the peripheral-based metrics, which I feel is sufficient to elevate them above RAR leader Buehler. It’s worth noting that Burnes was the leader in all three of the RA metrics, but Wheeler led the league with 213 innings while Burnes was nineteenth with 167. I suspect Burnes will win the actual vote, and while it’s tempting to side with the guy with spectacular rate stats, a 46 inning gap is enormous.

AL MVP:

1. DH/SP Shohei Ohtani, LAA

2. 1B Vladimir Guerrero, TOR

3. 1B Matt Olson, OAK

4. 2B Marcus Semien, TOR

5. 3B Jose Ramirez, CLE

6. SS Carlos Correa, HOU

7. RF Aaron Judge, NYA

8. SP Robbie Ray, TOR

9. RF Kyle Tucker, HOU

10. 2B Brandon Lowe, TB

A first baseman and a DH are the two AL offensive RAR leaders in a season in which no pitcher comes close to a top of the MVP ballot performance. The first baseman hits .305/.394/.589 to the DH’s .256/.372/.589, over 59 additional plate appearances. Under these circumstances, how can the first baseman possible rank second on the ballot, and a distant second at that? When the DH also pitches 130 innings with a RRA 31% lower than league average.

This should seem like a fairly obvious conclusion, and I suspect that Ohtani will handily win the award, but whether out of the need to generate “controversial” content or some other explanation that would indict their mental faculties, talking heads have spent a great deal of time pretending that this was a reasonable debate. I thought it would have been quite fascinating to see Guerrero win the triple crown as a test case of whether twice in a decade the mystical deference to the traditional categories could deny an Angel having a transcendent season of a MVP award.

For the rest of the ballot, if you take the fielding metrics at face value, you can make the case that Marcus Semien was actually the Most Valuable Blue Jay; I do not, with Carlos Correa serving as a prime example. He was +21 in DRS but only +3 in UZR, which is the difference between leading the league in position player bWAR and slotting seventh on my ballot (as he would fall behind Judge if I went solely on UZR). 

The omission of Salvardor Perez will certainly be a deviation from the actual voting. Perez’ OBA was just .315, and despite 48 homers he created “just” 99 runs. Worse yet, his defensive value was -13 runs per Baseball Prospectus. I would rank him not just behind the ten players listed, but Cedric Mullins, Bo Bichette, Xander Bogaerts, Yasmani Grandal, Rafael Devers, and a slew of starting pitchers. I don’t think he was one of the twenty most valuable players in the AL.

NL MVP:

1. RF Juan Soto, WAS

2. RF Bryce Harper, PHI

3. SS Trea Turner, WAS/LA

4. SP Zack Wheeler, PHI

5. SS Fernando Tatis, SD

6. SP Corbin Burnes, MIL

7. SP Walker Buehler, LA

8. 1B Paul Goldschmidt, STL

9. RF Tyler O’Neill, STL

10. SP Brandon Woodruff, MIL

Having not carefully examined the statistics during the season, two things surprised me about this race, which it was quickly apparent would come down to the well-matched right fielders, each of whom were among the best young players ever when they burst on the scene, one of whom inherited the other’s job more or less, and both of whom still toil in the same division. The first was that Soto, despite his dazzling OBA, actually ranked a smidge behind Harper offensively; the second was that Soto had a significant advantage in the fielding metrics that elevated him to the top.

Taking the more straightforward comparison first, Soto and Harper had essentially the same batting average (I’m ignoring park factors as WAS and PHI helpfully had a 101 PF, so it won’t change the comparison between the two), .313 to .309. Soto had the clear edge in W+HB rate despite the pair ranking one-two in the NL (22.7% of PA to Harper’s 17.8%), while Harper had a sizeable edge in isolated power (.305 to .221; Harper had only six more homers than Soto, but 22 more doubles). The walks and power essentially cancel out (Harper had a .520 Secondary Average to Soto’s .514, again ranking one-two in the circuit). Each created 116 runs, but despite his OBA edge Soto made twelve more outs as he had fifty six  more plate appearances. That leaves Harper with a narrow two RAR lead.

Fangraphs estimates that Soto’s non-steal baserunning was one run better than average, Harper’s zero. So it comes down to fielding, where Soto has +3 DRS and +2 UZR to Harper’s -6/+2. As a crude combination with regression to put the result on an equal footing with offensive value, I typically sum the two and divide by four, which leaves Soto +1 and Harper -1, to create a total value difference of two runs in favor of Soto.

Obviously, this difference is so narrow that one should barely even feel the need to address a choice to put Harper on top of their ballot. One could easily reason that the Phillies were in the race, and Harper contributed to keeping them in said race with his September/October performance (1157 September OPS). But I have been pretty consistent in not giving any consideration to a team’s position in the standings, so my only sanity check was to take a closer look at fielding using very crude but accessible metrics. My non-scientific impression would be that Harper might be something like a B- fielder and Soto a C.

I looked at the putout rate for each, dividing putouts by team AB – HR – K – A + SF (this essentially defines the outfielder’s potential plays as any balls including hits put in play, removing plays actually made by infielders of which assists serve as an approximation. Obviously there is much that is not considered even that might be approximated from the standard Baseball Guide data, like actual GB/FB ratio, handedness of pitchers and opposing batters, etc.) and multiplying by each player’s innings in the outfield divided by the team’s total innings. Viewed in this manner, Soto made a putout on 13.7% of potential plays to Harper’s 11.2%. 

A second crude check which may be free of unknown team-level biases but that introduces its own problems in that the other players are very different is to compare each player’s putout rate to that of his team’s other right fielders. For this, we can just look at per 9 innings as we have to assume that the other team level inputs in our putout % (HR, K, A, SF) were uniformly distributed between Soto/Harper’s innings and those played by other Nationals/Phillies right fielders. Soto recorded 2.17 PO/9 innings while other Nationals RF recorded 1.98: Harper 1.64 to other Phillies 1.51, so Soto recorded 10% more putouts than his teammates and Harper 9%.

Is any of this remotely conclusive? Of course not, but it is sufficient to convince me that the proposition that “Juan Soto was two runs more valuable than Bryce Harper in the field” is reasonable, and that in turn is enough to make Soto seem a whisker more valuable than Harper. It’s a very close race, much more interesting than the more discussed AL race (which in truth is interesting only because of Ohtani’s remarkable season and not any comparison to other players). 

I think the rest of the ballot follows RAR very closely with the pitchers mixed in. Max Scherzer ranked ahead of Brandon Woodruff on my Cy Young list, but they flip here as Woodruff was merely bad offensively (-1 run created); Scherzer didn’t reach base in 59 plate appearances (-5).

Rate Stat Series, pt. 14: Relativity for the Theoretical Team Framework

Before jumping into win-equivalent rate stats for the theoretical team framework, I think it would be helpful to re-do our theoretical team calculations on a purely rate basis. This is, after all, a rate stat series. In discussing the TT framework in pts. 9-11, I started by using the player’s PA to define the PA of the team, as Bill James chose to do with his TT Runs Created. This allowed our initial estimate of runs created or RAA to remain grounded in the player’s actual season. 

An alternative (and as we will see, equivalent) approach would be to eschew all of the “8*PA” and just express everything in rates to begin with. When originally discussing TT, I didn’t show it that way, but maybe I should have. I found that my own thinking when trying to figure out the win equivalent TT rates was greatly aided by walking through this process first.

Again, everything is equivalent to what we did before – if you just divide a lot of those equations by PA, you will get to the same place a lot quicker than I’m going to. The theoretical team framework we’re working with assumes that the batter gets 1/9 of the PA for the theoretical team. It’s also mathematically true that for Base Runs:

BsR/PA = (A*B/(B+C) + D)/PA = (A/PA)*(B/PA)/(B/PA + C/PA) + D/PA

If for the sake of writing formulas we rename A/PA as ROBA (Runners On Base Average), B/PA as AF (Advancement Factor; I’ve been using this abbreviation long before it came into mainstream usage in other contexts), C/PA as OA (Out Average), and D/PA as HRPA (Home Runs/PA), we can then write:

BsR/PA = ROBA*AF/(AF + OA) + HRPA

Since it is also true that R/O = R/PA/(1 – OBA), in this case it is true that:

BsR/O = (BsR/PA)/OA

We can use these equations to calculate the Base Runs per out for a theoretical team (I’m going to skip over “reference team” notation and just assume that the reference team is a league average team):

TT_ROBA = 1/9*ROBA + 8/9*LgROBA

TT_AF = 1/9*AF + 8/9*LgAF

TT_OA = 1/9*OA + 8/9*LgOA

TT_HRPA = 1/9*HRPA + 8/9*LgHRPA

TT_BsR/PA = TT_ROBA*TT_AF/(TT_AF + TT_OA) + TT_HRPA

TT_BsR/O = (TT_ROBA*TT_AF/(TT_AF + TT_OA) + TT_HRPA)/TT_OA

Here’s a sample calculation for 1994 Frank Thomas:

To calculate a win-equivalent rate stat, we can use the TT_BsR/O figure as a starting point (it suggests that a theoretical team of 1/9 Thomas and 8/9 league average would score .2344 runs/out). We don’t need to go through this additional calculation, though; when we calculated R+/O+ (or R+/PA+, RAA+/O+, or RAA+/PA+), we already had everything we needed for this calculation.

You will see if you do the math that:

TT_BsR/O = (RAA+/O+)*(1/9) + LgR/O

or

TT_BsR/O = (R+/O+)*(1/9) + (LgR/O)*(8/9)

or

TT_BsR/O = (RAA+/PA+)/(1 – LgOBA)*(1/9) + LgR/O

or 

TT_BsR/O = (R+/PA+)/(1 - LgOBA)*(1/9) + (LgR/O)*(8/9)

You could view this as a validation of the R+/O+ approach, as it does what it set out to do, which is to isolate the batter’s contribution to the theoretical team’s runs/out. Once we’ve established the team’s runs/out, it is pretty simple to convert to wins. I will just give formulas as I think they are pretty self-explanatory:

TT_BsR/G = TT_BsR/O*LgO/G

TT_RPG = TT_BsR/G + LgR/G

TT_x = TT_RPG^.29

TT_W% = (TT_BsR/G)^TT_x/((TT_BsR/G)^TT_x + (LgR/G)^TT_x)

Walking through this for the Franks, we have:

One thing to note here is that if we look at the theoretical team’s R/O (or R/G) relative to the league average, subtract one, multiply by nine, and add one back in, we will Thomas and Robinson’s relative R+/O+. This is not a surprising result given what we saw above regarding the relationship between R+/O+ and theoretical team R/O.

We now have a W% for the theoretical team, which we could leave alone as a rate stat, but it’s not very satisfying to me to have an individual rate stat expressed as a team W%. If we subtract .5, we have WAA/Team G; we could interpret this as meaning that Thomas is estimated to add .0609 wins per game and Robinson .0546 to a theoretical team on which they get 1/9 of PA. Another option would be to convert this WAA back to a total, defining “games” as PA/Lg(PA/G), and then we could have WAA+/PA+ or WAA+/O+ as rates. 

In keeping with the general format established in this series, though, my final answer for a win-equivalent rate stat for the TT framework will be to convert the winning percentage (actually, we’ll use win ratio since it  makes the math easier) back to the reference environment, and calculate a relative adjusted R+/O+. Since everything will be on an outs basis (as we’re using O+), we don’t need to worry about league PA/G when calculating our relative adjusted R+/O+.

Instead of calculating TT_W%, we could have left it in the form of team win ratio:

TT_WR = ((TT_BsR/G)/(LgR/G))^(TT_x)

We can convert this back to an equivalent run ratio in the reference environment (which for this series we’ve defined as having Pythagorean exponent r = 1.881) by solving for AdjTT_RR in the equation:

TT_WR = AdjTT_RR^r

so 

AdjTT_RR = TT_WR^(1/r)

We could convert this run ratio back to a team runs/game in the reference environment, and then to a team runs/out, and then use our equation for tying individual R+/O+ to theoretical team R/O to get an equivalent R+/O+ ratio. But why bother with all that, when we will just end up dividing it by the reference environment R/O to get our relative adjusted R+/O+? I noted above that there was a direct relationship between the theoretical team’s run ratio (which is equal to the theoretical team’s R/O divided by league R/O) and the batter’s relative R+/O+:

Rel R+/O+ = (TT_RR – 1)*9 + 1

So our Relative Adjusted R+/O+ can be calculated as:

RelAdj R+/O+ = (AdjTT_RR  - 1)*9 + 1

I brought back our original relative R+/O+ (prior to going through the win-equivalent math) for comparison. Thomas gains slightly and Robinson loses more, because the value of his relative runs is lower in a high scoring environment. This is a similar conclusion to what we saw when comparing relative R+/PA and the relative adjusted R+/PA for Robinson and Thomas. Nominal runs are more valuable when the run scoring environment is lower, because it takes fewer marginal runs to create a marginal win. Relative runs are more valuable when the scoring environment is higher, because the win ratio expected to result from a given run ratio increases due to the higher Pythagenpat exponent.

At this point, we have exhausted my thoughts and ideas concerning the theoretical issues in designing individual batter rate stats. Next time I will discuss mixing up our rate stats and the frameworks within which I assert each should ideally be used.

End of Season Statistics, 2021

While this edition of End of Season Statistics will more closely resemble the reports I published through 2019 than the 2020 edition did, there are still a number of issues created by the revised rules, particularly the extra innings rule and seven-inning doubleheaders. Seeing as that both of these changes could be walked back for 2022, I have not attempted to revise my approach to take them into account – should they become permanent, then and only then will I invest time in trying to make the necessary adjustments (some of which I outlined here) to fit the data they produce within traditional sabermetric structures.

In the mean time, there will be three main consequences of the rules:

1) While I will provide relief pitcher statistics this year, I will base the value metrics on eRA rather than RA or ERA. RA is hopelessly polluted by the Manfred runners, while ERA is hopelessly polluted by virtue of being ERA. While I would prefer to base the value metric on a measure that reflects runs actually allowed, they are messy enough to begin with in the case of relievers that I am not too concerned about it.

2) When computing value metrics for starting pitchers, I will be comparing their RRA to the estimated league average RA rather than the actual one, since the latter is polluted by Manfred runners even though starters’ statistics themselves are immune from the impact. 

3) Team run per game metrics will be expressed per 9 innings (27 outs), and a per 9 innings approach will be used to calculate expected winning percentages. As such, these will not exactly be an attempt to estimate what any given team’s W% should have been, but rather a theoretical estimate of what their W% would have been had they been playing under normal rules. For actual runs and runs allowed, these will still be distorted by Manfred runners, but accounting for that is again much more trouble than a (hopefully) two-year interlude justifies.

The data comes from a number of different sources. Most of the data comes from Baseball-Reference; I will try to note exceptions as they come up.

The basic philosophy behind these stats is to use the simplest methods that have acceptable accuracy. Of course, "acceptable" is in the eye of the beholder, namely me. I use Pythagenpat not because other run/win converters, like a constant RPW or a fixed exponent are not accurate enough for this purpose, but because it's mine and it would be kind of odd if I didn't use it.

If I seem to be a stickler for purity in my critiques of others' methods, I'd contend it is usually in a theoretical sense, not an input sense. So when I exclude hit batters, I'm not saying that hit batters are worthless or that they *should* be ignored; it's just easier not to mess with them and not that much less accurate (note: hit batters are actually included in the offensive statistics now).

I also don't really have a problem with people using sub-standard methods (say, Basic RC) as long as they acknowledge that they are sub-standard. If someone pretends that Basic RC doesn't undervalue walks or cause problems when applied to extreme individuals, I'll call them on it; if they explain its shortcomings but use it regardless, I accept that. Take these last three paragraphs as my acknowledgment that some of the statistics displayed here have shortcomings as well, and I've at least attempted to describe some of them in the discussion below.

The League spreadsheet is pretty straightforward--it includes league totals and averages for a number of categories, most or all of which are explained at appropriate junctures throughout this piece. The advent of interleague play has created two different sets of league totals--one for the offense of league teams and one for the defense of league teams. Before interleague play, these two were identical. I do not present both sets of totals (you can figure the defensive ones yourself from the team spreadsheet, if you desire), just those for the offenses. The exception is for the defense-specific statistics, like innings pitched and quality starts. The figures for those categories in the league report are for the defenses of the league's teams. However, I do include each league's breakdown of basic pitching stats between starters and relievers (denoted by "s" or "r" prefixes), and so summing those will yield the totals from the pitching side. 

I added a column this year for “ActO”, which is actual (rather than estimated) outs made by the team offensively. This can be determined from the official statistics as PA – R – LOB. I have then replaced the column I usually show for league R/G (“N”) with R/9, which is actually R*27/ActO, which is equivalent to R*9/IP. This restates the league run average in the more familiar per nine innings. I’ve done the same for “OG”, which is Outs/Game but only for those outs I count in the individual hitter’s stats (AB – H + CS) ,“PA/G”, which is normally just (AB + W)/G, and “KG” and “WG” (normally just K/G and W/G) – these are now “O/9”, “PA/9”, still “KG”/”WG” and are per 27 actual outs.

The Team spreadsheet focuses on overall team performance--wins, losses, runs scored, runs allowed. The columns included are: Park Factor (PF), Winning Percentage (W%), Expected W% (EW%), Predicted W% (PW%), wins, losses, runs, runs allowed, Runs Created (RC), Runs Created Allowed (RCA), Home Winning Percentage (HW%), Road Winning Percentage (RW%) [exactly what they sound like--W% at home and on the road], R/9, RA/9, Runs Created/9 (RC/9), Runs Created Allowed/9 (RCA/9), and Runs Per Game (the average number of runs scored an allowed per game). For the offensive categories, runs/9 are based on runs per 27 actual outs; for pitching categories, they are runs/9 innings.

I based EW% and PW% on R/9 and RA/9 (and RC/9 and RCA/9) rather than the actual runs totals. This means that what they are not estimating what a team’s winning percentage should have been in the actual game constructions that they played, but what they should have been if playing nine inning games but scoring/allowing runs at the same rate per inning. EW%, which is based on actual R and RA, is also polluted by inflated runs in extra inning games; PW%, which is based on RC and RCA, doesn’t suffer from this distortion.

The runs and Runs Created figures are unadjusted, but the per-game averages are park-adjusted, except for RPG which is also raw. Runs Created and Runs Created Allowed are both based on a simple Base Runs formula. The formula is:

A = H + W - HR - CS

B = (2TB - H - 4HR + .05W + 1.5SB)*.76

C = AB - H

D = HR

Naturally, A*B/(B + C) + D.

Park factors are based on five years of data when applicable (so 2017 - 2021), include both runs scored and allowed, and they are regressed towards average (PF = 1), with the amount of regression varying based on the number of games in total in the sample. There are factors for both runs and home runs. The initial PF (not shown) is:

iPF = (H*T/(R*(T - 1) + H) + 1)/2

where H = RPG in home games, R = RPG in road games, T = # teams in league (14 for AL and 16 for NL). Then the iPF is converted to the PF by taking x*iPF + (1-x), where x = .1364*ln(G/162) + .5866. I will expound upon how this formula was derived in a future post. 

It is important to note, since there always seems to be confusion about this, that these park factors already incorporate the fact that the average player plays 50% on the road and 50% at home. That is what the adding one and dividing by 2 in the iPF is all about. So if I list Fenway Park with a 1.02 PF, that means that it actually increases RPG by 4%.

In the calculation of the PFs, I did not take out “home” games that were actually at neutral sites (of which there were a rash in 2020). The Blue Jays multiple homes make things very messy, so I just used their 2021 data only. 

There are also Team Offense and Defense spreadsheets. These include the following categories:

Team offense: Plate Appearances, Batting Average (BA), On Base Average (OBA), Slugging Average (SLG), Secondary Average (SEC), Walks and Hit Batters per At Bat (WAB), Isolated Power (SLG - BA), R/G at home (hR/G), and R/G on the road (rR/G) BA, OBA, SLG, WAB, and ISO are park-adjusted by dividing by the square root of park factor (or the equivalent; WAB = (OBA - BA)/(1 - OBA), ISO = SLG - BA, and SEC = WAB + ISO).

Team defense: Innings Pitched, BA, OBA, SLG, Innings per Start (IP/S), Starter's eRA (seRA), Reliever's eRA (reRA), Quality Start Percentage (QS%), RA/G at home (hRA/G), RA/G on the road (rRA/G), Battery Mishap Rate (BMR), Modified Fielding Average (mFA), and Defensive Efficiency Record (DER). BA, OBA, and SLG are park-adjusted by dividing by the square root of PF; seRA and reRA are divided by PF.

The three fielding metrics I've included are limited it only to metrics that a) I can calculate myself and b) are based on the basic available data, not specialized PBP data. The three metrics are explained in this post, but here are quick descriptions of each:

1) BMR--wild pitches and passed balls per 100 baserunners = (WP + PB)/(H + W - HR)*100

2) mFA--fielding average removing strikeouts and assists = (PO - K)/(PO - K + E)

3) DER--the Bill James classic, using only the PA-based estimate of plays made. Based on a suggestion by Terpsfan101, I've tweaked the error coefficient. Plays Made = PA - K - H - W - HR - HB - .64E and DER = PM/(PM + H - HR + .64E)

Next are the individual player reports. I defined a starting pitcher as one with 15 or more starts. All other pitchers are eligible to be included as a reliever. If a pitcher has 40 appearances, then they are included. Additionally, if a pitcher has 50 innings and less than 50% of his appearances are starts, he is also included as a reliever (this allows some swingmen type pitchers who wouldn’t meet either the minimum start or appearance standards to get in). This would be a good point to note that I didn't do much to adjust for the opener--I made some judgment calls (very haphazard judgment calls) on which bucket to throw some pitchers in. This is something that I should definitely give some more thought to in coming years.

For all of the player reports, ages are based on simply subtracting their year of birth from 2021. I realize that this is not compatible with how ages are usually listed and so “Age 27” doesn’t necessarily correspond to age 27 as I list it, but it makes everything a heckuva lot easier, and I am more interested in comparing the ages of the players to their contemporaries than fitting them into historical studies, and for the former application it makes very little difference. The "R" category records rookie status with a "R" for rookies and a blank for everyone else. Also, all players are counted as being on the team with whom they played/pitched (IP or PA as appropriate) the most.

For relievers, the categories listed are: Games, Innings Pitched, estimated Plate Appearances (PA), Run Average (RA), Relief Run Average (RRA), Earned Run Average (ERA), Estimated Run Average (eRA), DIPS Run Average (dRA), Strikeouts per Game (KG), Walks per Game (WG), Guess-Future (G-F), Inherited Runners per Game (IR/G), Batting Average on Balls in Play (%H), Runs Above Average (RAA), and Runs Above Replacement (RAR).

IR/G is per relief appearance (G - GS); it is an interesting thing to look at, I think, in lieu of actual leverage data. You can see which closers come in with runners on base, and which are used nearly exclusively to start innings. Of course, you can’t infer too much; there are bad relievers who come in with a lot of people on base, not because they are being used in high leverage situations, but because they are long men being used in low-leverage situations already out of hand.

For starting pitchers, the columns are: Wins, Losses, Innings Pitched, Estimated Plate Appearances (PA), RA, RRA, ERA, eRA, dRA, KG, WG, G-F, %H, Pitches/Start (P/S), Quality Start Percentage (QS%), RAA, and RAR. RA and ERA you know--R*9/IP or ER*9/IP, park-adjusted by dividing by PF. The formulas for eRA and dRA are based on the same Base Runs equation and they estimate RA, not ERA.

* eRA is based on the actual results allowed by the pitcher (hits, doubles, home runs, walks, strikeouts, etc.). It is park-adjusted by dividing by PF.

* dRA is the classic DIPS-style RA, assuming that the pitcher allows a league average %H, and that his hits in play have a league-average S/D/T split. It is park-adjusted by dividing by PF.

The formula for eRA is:

A = H + W - HR

B = (2*TB - H - 4*HR + .05*W)*.78

C = AB - H = K + (3*IP - K)*x (where x is figured as described below for PA estimation and is typically around .93) = PA (from below) - H - W

eRA = (A*B/(B + C) + HR)*9/IP

To figure dRA, you first need the estimate of PA described below. Then you calculate W, K, and HR per PA (call these %W, %K, and %HR). Percentage of balls in play (BIP%) = 1 - %W - %K - %HR. This is used to calculate the DIPS-friendly estimate of %H (H per PA) as e%H = Lg%H*BIP%.

Now everything has a common denominator of PA, so we can plug into Base Runs:

A = e%H + %W

B = (2*(z*e%H + 4*%HR) - e%H - 5*%HR + .05*%W)*.78

C = 1 - e%H - %W - %HR

cRA = (A*B/(B + C) + %HR)/C*a

z is the league average of total bases per non-HR hit (TB - 4*HR)/(H - HR), and a is the league average of (AB - H) per game.

Also shown are strikeout and walk rate, both expressed as per game. By game I mean not nine innings but rather the league average of PA/G. I have always been a proponent of using PA and not IP as the denominator for non-run pitching rates, and now the use of per PA rates is widespread. Usually these are expressed as K/PA and W/PA, or equivalently, percentage of PA with a strikeout or walk. I don’t believe that any site publishes these as K and W per equivalent game as I am here. This is not better than K%--it’s simply applying a scalar multiplier. I like it because it generally follows the same scale as the familiar K/9.

To facilitate this, I’ve finally corrected a flaw in the formula I use to estimate plate appearances for pitchers. Previously, I’ve done it the lazy way by not splitting strikeouts out from other outs. I am now using this formula to estimate PA (where PA = AB + W):

PA = K + (3*IP - K)*x + H + W

Where x = league average of (AB - H - K)/(3*IP - K)

Then KG = K*Lg(PA/G) and WG = W*Lg(PA/G).

G-F is a junk stat, included here out of habit because I've been including it for years. It was intended to give a quick read of a pitcher's expected performance in the next season, based on eRA and strikeout rate. Although the numbers vaguely resemble RAs, it's actually unitless. As a rule of thumb, anything under four is pretty good for a starter. G-F = 4.46 + .095(eRA) - .113(K*9/IP). It is a junk stat. JUNK STAT JUNK STAT JUNK STAT. Got it?

%H is BABIP, more or less--%H = (H - HR)/(PA - HR - K - W), where PA was estimated above. Pitches/Start includes all appearances, so I've counted relief appearances as one-half of a start (P/S = Pitches/(.5*G + .5*GS). QS% is just QS/(G - GS); I don't think it's particularly useful, but Doug's Stats include QS so I include it.

I've used a stat called Relief Run Average (RRA) in the past, based on Sky Andrecheck's article in the August 1999 By the Numbers; that one only used inherited runners, but I've revised it to include bequeathed runners as well, making it equally applicable to starters and relievers. One thing that's become more problematic as time goes on for calculating this expanded metric is the sketchy availability of bequeathed runner data for relievers. As a result, only bequeathed runners left by starters (and "relievers" when pitching as starters) are taken into account here. I use RRA as the building block for baselined value estimates for all pitchers. I explained RRA in this article, but the bottom line formulas are:

BRSV = BRS - BR*i*sqrt(PF)

IRSV = IR*i*sqrt(PF) - IRS

RRA = ((R - (BRSV + IRSV))*9/IP)/PF

Given the difficulties of looking at the league average of actual runs due to Manfred rules, I decided to use eRA to calculate the baselined metrics for relievers. So they are no longer based on actual runs allowed by the pitcher, but rather on the component statistics. For starters, I will use the actual runs allowed in the form of RRA, but compared to the league average eRA. Starters’ statistics are not influenced by the Manfred runners, but the league average RA is still artificially inflated by them, so the league eRA should be a better measure of what the league average RRA would be in lieu of Manfred runners. I say “should” as this assumes that the eRA formula is properly calibrated, and it’s hard to calibrate any runs created formula when you don’t know what the league average runs should be. I remain unconvinced that most saberemtricians have fully grasped all of the implications of the Manfred runners on the 2020-2021 statistics, and if these rules are maintained going forward it will require much more effort to maintain basic sabermetric measures. In any event, the RAA/RAR formulas I’m using are:

RAA (relievers) = (.951*Lg(eRA) - eRA)*IP/9

RAA (starters) = (1.025*Lg(eRA) - eRA)*IP/9

RAR (relievers) = (1.11*Lg(eRA) - RRA)*IP/9

RAR (starters) = (1.28*Lg(eRA) - RRA)*IP/9

All players with 250 or more plate appearances (official, total plate appearances) are included in the Hitters spreadsheets (along with some players close to the cutoff point who I was interested in). Each is assigned one position, the one at which they appeared in the most games. The statistics presented are: Games played (G), Plate Appearances (PA), Outs (O), Batting Average (BA), On Base Average (OBA), Slugging Average (SLG), Secondary Average (SEC), Runs Created (RC), Runs Created per Game (RG), Speed Score (SS), Hitting Runs Above Average (HRAA), Runs Above Average (RAA), and Runs Above Replacement (RAR).

Starting in 2015, I'm including hit batters in all related categories for hitters, so PA is now equal to AB + W+ HB. Outs are AB - H + CS. BA and SLG you know, but remember that without SF, OBA is just (H + W + HB)/(AB + W + HB). Secondary Average = (TB - H + W + HB)/AB = SLG - BA + (OBA - BA)/(1 - OBA). I have not included net steals as many people (and Bill James himself) do, but I have included HB which some do not.

BA, OBA, and SLG are park-adjusted by dividing by the square root of PF. This is an approximation, of course, but I'm satisfied that it works well (I plan to post a couple articles on this some time during the offseason). The goal here is to adjust for the win value of offensive events, not to quantify the exact park effect on the given rate. I use the BA/OBA/SLG-based formula to figure SEC, so it is park-adjusted as well.

Runs Created is actually Paul Johnson's ERP, more or less. Ideally, I would use a custom linear weights formula for the given league, but ERP is just so darn simple and close to the mark that it’s hard to pass up. I still use the term “RC” partially as a homage to Bill James (seriously, I really like and respect him even if I’ve said negative things about RC and Win Shares), and also because it is just a good term. I like the thought put in your head when you hear “creating” a run better than “producing”, “manufacturing”, “generating”, etc. to say nothing of names like “equivalent” or “extrapolated” runs. None of that is said to put down the creators of those methods--there just aren’t a lot of good, unique names available.

For 2015, I refined the formula a little bit to:

1. include hit batters at a value equal to that of a walk

2. value intentional walks at just half the value of a regular walk

3. recalibrate the multiplier based on the last ten major league seasons (2005-2014)

This revised RC = (TB + .8H + W + HB - .5IW + .7SB - CS - .3AB)*.310

RC is park adjusted by dividing by PF, making all of the value stats that follow park adjusted as well. RG, the Runs Created per Game rate, is RC/O*26. For a very long time, dating back to the Jamesian era, 25.5 has been a good approximation for the number of (AB – H + CS) per game, but it has been creeping up, and per 9 innings this year it was right around 26, so I am using that value now. 

I do not believe that outs are the proper denominator for an individual rate stat, but I also do not believe that the distortions caused are that bad. (I still intend to finish my rate stat series and discuss all of the options in excruciating detail, but alas you’ll have to take my word for it now).

Several years ago I switched from using my own "Speed Unit" to a version of Bill James' Speed Score; of course, Speed Unit was inspired by Speed Score. I only use four of James' categories in figuring Speed Score. I actually like the construct of Speed Unit better as it was based on z-scores in the various categories (and amazingly a couple other sabermetricians did as well), but trying to keep the estimates of standard deviation for each of the categories appropriate was more trouble than it was worth.

Speed Score is the average of four components, which I'll call a, b, c, and d:

a = ((SB + 3)/(SB + CS + 7) - .4)*20

b = sqrt((SB + CS)/(S + W))*14.3

c = ((R - HR)/(H + W - HR) - .1)*25

d = T/(AB - HR - K)*450

James actually uses a sliding scale for the triples component, but it strikes me as needlessly complex and so I've streamlined it. He looks at two years of data, which makes sense for a gauge that is attempting to capture talent and not performance, but using multiple years of data would be contradictory to the guiding principles behind this set of reports (namely, simplicity. Or laziness. You're pick.) I also changed some of his division to mathematically equivalent multiplications.

The baselined stats are calculated in the same basic manner the pitcher stats are, using the league average RG:

HRAA = (RG – LgRG)*O/26

RAA = (RG – LgRG*PADJ)*O/26

RAR = (RG – LgRG*PADJ*.73)*O/26

PADJ is the position adjustment, based on 2010-2019 offensive data. For catchers it is .92; for 1B/DH, 1.14; for 2B, .99; for 3B, 1.07; for SS, .95; for LF/RF, 1.09; and for CF, 1.05. As positional flexibility takes hold, fielding value is better quantified, and the long-term evolution of the game continues, it's right to question whether offensive positional adjustments are even less reflective of what we are trying to account for than they were in the past. But while I do not claim that the relationship is or should be perfect, at the level of talent filtering that exists to select major leaguers, there should be an inverse relationship between offensive performance by position and the defensive responsibilities of the position. Not a perfect one, but a relationship nonetheless. An offensive positional adjustment than allows for a more objective approach to setting a position adjustment. Again, I have to clarify that I don’t think subjectivity in metric design is a bad thing - any metric, unless it’s simply expressing some fundamental baseball quantity or rate (e.g. “home runs” or “on base average”) is going to involve some subjectivity in design (e.g linear or multiplicative run estimator, any myriad of different ways to design park factors, whether to include a category like sacrifice flies that is more teammate-dependent).

The replacement levels I have used here are very much in line with the values used by other sabermetricians. This is based both on my own "research", my interpretation of other's people research, and a desire to not stray from consensus and make the values unhelpful to the majority of people who may encounter them.

Replacement level is certainly not settled science. There is always going to be room to disagree on what the baseline should be. Even if you agree it should be "replacement level", any estimate of where it should be set is just that--an estimate. Average is clean and fairly straightforward, even if its utility is questionable; replacement level is inherently messy. So I offer the average baseline as well.

For position players, replacement level is set at 73% of the positional average RG (since there's a history of discussing replacement level in terms of winning percentages, this is roughly equivalent to .350). For starting pitchers, it is set at 128% of the league average RA (.380), and for relievers it is set at 111% (.450).

The spreadsheets are published as Google Spreadsheets, which you can download in Excel format by changing the extension in the address from "=html" to "=xlsx", or in open format as "=ods", or in csv as "=csv". That way you can download them and manipulate things however you see fit.

League -- 2021

Park Factors -- 2021

Teams -- 2021

Team Defense -- 2021

Team Offense -- 2021

AL Relievers -- 2021

NL Relievers -- 2021

AL Starters -- 2021

NL Starters -- 2021

AL Hitters -- 2021

NL Hitters -- 2021

Crude Playoff Odds--2021

These are very simple playoff odds, based on my crude rating system for teams using an equal mix of W%, EW% (based on R/RA), PW% (based on RC/RCA), and 69 games of .500. They account for home field advantage by assuming a .500 team wins 54.2% of home games (major league average 2006-2015). They assume that a team's inherent strength is constant from game-to-game. They do not generally account for any number of factors that you would actually want to account for if you were serious about this, including but not limited to injuries, the current construction of the team rather than the aggregate seasonal performance, pitching rotations, estimated true talent of the players, etc.

The CTRs that are fed in are:

Wildcard game odds (the least useful since the pitching matchups aren’t taken into account, and that matters most when there is just one game):

DS:

LCS:

World Series:

Everything combined:

If the Dodgers win the wildcard game, they become the World Series favorites at 19.9%, with the Giants falling to 19.0%; the Rays fall to 16.1%, so the Dodgers don't have a huge impact on the AL odds (the Dodgers are given a 32.6% to win the pennant should they win the wildcard game). If the Cardinals win, the Giants jump to 25.9% and the Rays to 17.6% (of course the Giants benefit greatly because they have an estimated 68% chance to beat the Cardinals in the NLDS but only 50% to beat the Dodgers). Ranging into the realm of the subjective, I personally favor Houston to win the AL pennant and think Milwaukee will benefit from concentrating innings in front-line pitchers (even sans Devin Williams) and from being on the opposite side of the bracket from the NL West.

I don't have the energy for a rant about what a preposterous proposition it is to make the Dodgers play the Cardinals, or about how the much-hyped four-way battle for the AL wildcard yesterday would never happen under Rob Manfred's desired system (or how if it did it would be between teams struggling to reach .500). The playoffs simultaneously manage to be one of the best and worst things about baseball, and every expansion will serve to enhance the latter.

Rate Stat Series, pt. 13: Relativity for the Linear Weights Framework

Of the three frameworks for evaluating individual offense, linear weights offers the simplest calculation of runs created or RAA, but will be the hardest to convert to a win-equivalent rate – mentally if not computationally. In order to do this, we need to consider what our metrics actually represent and make our choices accordingly. The path that I am going to suggest is not inevitable – it makes sense to me, but there are certainly valid alternative paths.

In attempting to measure the win value of a batter’s performance in the linear weights framework, we could construct a theoretical team and measure his win impact on it. In so doing, one could argue that the batter’s tertiary impact (which would be ignored under such an approach) is immaterial, perhaps even illusory, and that the process of converting runs to wins is independent from the development of the run estimate. Thus we could use a static approach for estimating runs and a dynamic team approach for converting those runs to wins.

I would argue in turn that the most consistent approach is to continue to operate under the assumption that linear weights represents a batter’s impact on a team that is average once he is added to it, and thus not allow any dynamism in the runs to wins conversion. Since under this school of thought all teams are equal, whether we add Frank Thomas or Matt Walbeck, there is no need to account for how those players change the run environment and the run/win conversion – because they both ultimately operate in the same run environment.

One could argue that I am taking a puritanical viewpoint, and that this would become especially clear in a case in which one compared the final result of the linear weights framework to the final result of the theoretical team framework. As we’ve seen, RAA is very similar between the two approaches, but the run/win conversions will diverge more if in one case we ignore the batter’s impact on the run environment. In any event, the methodology we’ll use for the theoretical team framework will be applicable to linear weights as well, if you desire to use it.

Since we will not be modeling any dynamic impact of the batter upon the team’s run environment, it is an easy choice to start with RAA and convert it to wins above average (WAA) by dividing by a runs per win (RPW) value. An example of this is the rule of thumb that 10 runs = 1 win, so 50 RAA would be worth 5 WAA. 

There are any number of methods by which we could calculate RPW, and a couple philosophical paths to doing so. On the latter, I’m assuming that we want our RPW to be represent the best estimate of the number of marginal runs it would take for a .500 team (or more precisely a team with R = RA) to earn a marginal win. Since I’ve presumed that Pythagenpat is the correct run to win conversion, the most consistent is to use the RPW implied by Pythagenpat, which is:

RPW = 2*RPG^(1 – z) where z is the Pythagenpat exponent

so when z = .29, RPW = 2*RPG^.71

For the 1966 AL, this produces 8.588 RPW and for the 1994 AL it is 10.584. So we can calculate LW_WAA = LW_RAA/RPW, and LW_WAA/PA seems like the natural choice for a rate stat:

This tightens the gap between Robinson and Thomas as compared to a RAA/PA comparison, and since we’ve converted to wins, we can look at WAA/PA without having to worry about the underlying contextual differences (note: this is actually not true, but I’m going to pretend like it is for a little bit for the sake of the flow of this discussion). 

There is another step we could take, which is to recognize that the Franks do influence the context in which their wins are earned, driving up their team’s RPGs and thus RPWs and thus their own WAAs. Again, I would contend that a theoretically pure linear weights framework assumes that the team is average after the player is added. Others would contend that by making that assertion I’m elevating individual tertiary offensive contributions to a completely unwarranted level of importance, ignoring a measurable effect of individual contribution because the methodology ignores an immaterial one. This is a perfectly fair critique, and so I will also show how we can adjust for the hitter’s impact on the team RPW in this step. Pete Palmer makes this adjustment as part of converting from Batting Runs (which is what I’m calling LW_RAA) to Batting Wins (what I’m calling LW_WAA), and far be it from me to argue too vociferously against Pete Palmer when it comes to a linear weights framework.

What Palmer would have you do next (conceptually as he uses a different RPW methodology) is take the batter’s RAA, divide by his games played, and add to RPG to get the RPG for an average team with the player in question added. It’s that simple because RPG already represents average runs scored per game by both teams and RAA already captures a batter’s primary and secondary contributions to his team’s offense. One benefit or drawback of this approach, depending on one’s perspective, is that unlike the theoretical team approach it is tethered to the player’s actual plate appearances/games. Using the theoretical team approach from this series, a batter always gets 1/9 of team PA. Under this approach, a batter’s real world team PA, place in the batting order, frequency of being removed from the game, etc. will have a slight impact on our estimate of his impact on an average team. We could also eschew using real games played, and instead use something like “team PA game equivalents”. For example, in the 1994 AL the average team had 38.354 PA/G; Thomas, with 508 PA, had the equivalent of 119.21 games for an average hitter getting 1/9 of an average team’s PA (508/38.354*9). I’ve used real games played, as Palmer did, in the examples that follow.

Applying the Palmerian approach to our RPW equation:

TmRPG = LgRPG + RAA/G

TmRPW = 2*TmRPG^.71

LW_WAA = LW_RAA/TmRPW

For the Franks, we get:

The difference between Thomas and Robinson didn’t change much, but both lose WAA and WAA/PA due to their effect on the team’s run environment as each run is less valuable as more are scored. 

I have used WAA/PA as a win-equivalent rate without providing any justification for doing so. In fact, there is very good theoretical reason for not doing so. One of the key underpinnings of all of our rate stats is that plate appearances are not fixed across contexts – they are a function of team OBA. Wins are fixed across contexts – always exactly one per game. Thus when we compare Robinson and Thomas, it’s not enough to simply look at WAA/PA; we also need to adjust for the league PA/G difference or else the denominator of our win-equivalent rate stat will distort the relativity we have so painstakingly tried to measure.

In the 1966 AL, teams averaged 36.606 PA/G; in 1994, it was 38.354. Imagine that we had two hitters from these leagues with identical WAA and PA. We don’t have to imagine it; in 1966 Norm Siebern had .847 WAA in 399 PA, and in 1994 Felix Jose had .845 WAA in 401 PA (I’m using Palmer-style WAA in this example). It seems that Siebern had a minuscule advantage over Jose. But while wins are fixed across contexts (one per game, regardless of the time and place), plate appearances are not. A batter using 401 PA in 1994 was taking a smaller share of the average PA than one taking 399 in 1966 (you might be yelling about the difference in total games played between the two leagues due to the strike, but remember that WAA already has taken into account the performance of an average player – whether over a 113 or 162 game team-season is irrelevant when comparing their WAA figures). In 1994, 401 PA represented 10.46 team games worth of PA; in 1966, 399 represented 10.90 worth. In fact, Siebern’s WAA rate was not higher than Jose’s; despite having two fewer PA, Siebern took a larger share of his team’s PA to contribute his .85 WAA than Jose did.

If we do not make a correction of this type and just use WAA/PA, we will be suggesting that the hitters of 1966 were more productive on a win-equivalent rate basis than the hitters of 1994 (although this is difficult to prove as by definition the average player’s WAA/PA will be 0, regardless of the environment in which they played). I don’t want to get bogged down in this discussion too much, so I will point you here for a discussion focused just on this aspect of comparing across league-seasons.

There are a number of different ways you could adjust for this; the “team games of PA” approach I used would be one. The approach I will use is to pick a reference PA/G, similar to our reference Pythagenpat exponent from the last installment, and force everyone to this scale. For all seasons 1961-2019, the average PA/G is 37.359 which I will define as refPA/G. The average R/G is 4.415, so the average RPG is 8.83 and the refRPW is 9.390.

If we calculate:

adjWAA/PA = WAA/PA * Lg(PA/G)/ref(PA/G)

Then we will have restated a hitter’s WAA rate in the reference environment. This is an option as our final linear weight win stat:

This increases Thomas’ edge over Robinson, while giving Jose a miniscule lead over Siebern. As a final rate stat, I find it a little unsatisfying for a couple of reasons:

1. while the ultimate objective of an offense is to contribute to wins, runs feels like a more appropriate unit

2. related to #1, wins compress the scale between hitters. There’s nothing wrong with this to the extent that it forces us to recognize that small differences between estimates fall squarely within the margin of error inherent to the exercise, but it makes quoting and understanding the figures more of a challenge.

3. WAA/PA, adjusted for PA context or not, is only differentially comparable; ideally we’d like to have a comparable ratio

My solution to this is to first convert adjusted WAA/PA to an adjusted RAA/PA, which takes care of objections #1 and 2, then to convert it to an adjusted R+/PA, which takes care of objection #3. At each stage we have a perfectly valid rate stat; it’s simply a matter of preference. 

To do this seems simple (let’s not get too attached to this approach, which we’ll revisit in a future post):

adjRAA/PA = adjWAA/PA*refRPW (remember, by adjusting WAA/PA using the refPA/G, we’ve restated everything in the terms of the reference league)

adjR+/PA = adjRAA/PA + ref(R/PA)  (reference R/PA is .1182, which can be obtained by dividing the ref R/G by the ref PA/G)

We can also compute a relative adjusted R+/PA:

reladjR+/PA = (adjR+/PA)/(ref(R/PA))

= ((RAA/PA)/TmRPW * Lg(PA/G)/ref(PA/G) * refRPW + Ref(R/PA))/Ref(R/PA)

= (RAA/PA)/TmRPW * Lg(PA/G)/ref(PA/G) * refRPW/ref(R/PA) + 1

I included raw R+/PA and its ratio the league average (relative R+/PA) to compare to this final relative adjusted R+/PA. For three of the players, the differences are small; it is only Frank Robinson whose standing is significantly diminished. This may seem counterintuitive, but remember that the more ordinary hitters have much smaller impact on RPW than the Franks. Relative to Thomas, Robinson gets more of a boost from his lower RPW (his team RPW was 19% lower than Thomas) than Thomas does from the PA adjustment (the 1994 AL had 4.8% more PA/G than the 1966 AL).

We could also return to the puritan approach (which I actually stubbornly favor for the linear weights framework) and make these adjustments as well. The equations are the same as above except where we use TmRPW, we will instead use LgRPW – reverting to assuming that the batter has no impact on the run/win conversion.

Here the impact on the Franks is similar; both are hurt of course when we consider their impact on TmRPW. Next time, we will quit messing around with half-measures – no more mixing linear run contributions with dynamic run/win converters. We’re going full theoretical team.