Run Distribution and W%, 2019

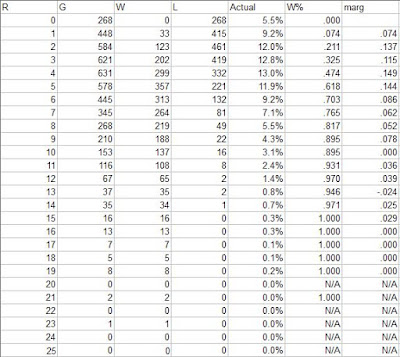
In 2019, the major league average was 4.83 runs/game. It was distributed thusly:



The “marg” column shows the marginal W% for each additional run scored. The mode of runs scored was four, and the fourth run was also the most valuable marginal run; 4.83 is a fairly high scoring environment and not surprisingly these are both higer than the comparable figures from recent seasons.

The Enby distribution (shown below for 4.85 R/G) did its usual decent job of estimating that distribution given the average; underestimating shutouts and one run games while underestimating the frequency of games with two to four runs scored is par for the course, but I dare say it’s still a respectable model:





One way that you can use Enby to examine team performance is to use the team’s actual runs scored/allowed distributions in conjunction with Enby to come up with an offensive or defensive winning percentage. The notion of an offensive winning percentage was first proposed by Bill James as an offensive rate stat that incorporated the win value of runs. An offensive winning percentage is just the estimated winning percentage for an entity based on their runs scored and assuming a league average number of runs allowed. While later sabermetricians have rejected restating individual offensive performance as if the player were his own team, the concept is still sound for evaluating team offense (or, flipping the perspective, team defense).

In 1986, James sketched out how one could use data regarding the percentage of the time that a team wins when scoring X runs to develop an offensive W% for a team using their run distribution rather than average runs scored as used in his standard OW%. I’ve been applying that concept since I’ve written this annual post, and last year was finally able to implement an Enby-based version. I will point you here if you are interested in the details of how this is calculated, but there are two main advantages to using Enby rather than the empirical distribution:

1. While Enby may not perfectly match how runs are distributed in the majors, it sidesteps sample size issues and data oddities that are inherent when using empirical data. Use just one year of data and you will see things like teams that score ten runs winning less frequently than teams that score nine. Use multiple years to try to smooth it out and you will no longer be centered at the scoring level for the season you’re examining.

2. There’s no way to park adjust unless you use a theoretical distribution. These are now park-adjusted by using a different assumed distribution of runs allowed given a league-average RA/G for each team based on their park factor (when calculating OW%; for DW%, the adjustment is to the league-average R/G).

I call these measures Game OW% and Game DW% (gOW% and gDW%). One thing to note about the way I did this, with park factors applied on a team-by-team basis and rounding park-adjusted R/G or RA/G to the nearest .05 to use the table of Enby parameters that I’ve calculated, is that the league averages don’t balance to .500 as they should in theory. The average gOW% is .489 and the average gDW% is .510.

For most teams, gOW% and OW% are very similar. Teams whose gOW% is higher than OW% distributed their runs more efficiently (at least to the extent that the methodology captures reality); the reverse is true for teams with gOW% lower than OW%. The teams that had differences of +/- 3 wins between the two metrics were (all of these are the g-type less the regular estimate, with the teams in descending order of absolute value of the difference):

Positive: None
Negative: HOU, OAK, LA

I used to show +/- 2, but with the league gOW% being .490, there’s nothing abnormal about a two win difference (at least on the negative side). Were I more concerned with analysis rather than the concept, I would take some stronger efforts to clean up this issue with more precise application of park factors and Enby coefficients, but I consider this post to be more of an annual demonstration of concept.

Teams with differences of +/- 3 defensive wins were:

Positive: PIT, MIL, SEA, BAL
Negative: None

I usually run a graph showing the actual v. Enby run distribution of the team with the biggest gap on offense or defense, which was Houston’s offense. However, I don’t find their situation particularly compelling, as they had a handful of games with a lot of runs scored, which is easy to understand. More interesting is Pittsburgh, whose defensive run distribution produced a .445 gDW% but only a .416 DW% (the graph shows the Enby probabilities for a team that allowed 5.6 R/G using c = .852, which is used to calculate the gOW%/gDW% estimates):



Even as someone who has looked at a lot of these, it's hard to articulate why this was a good thing for Pittsburgh (good in the sense that their runs allowed distribution should have resulted in more wins than a typical runs allowed distribution for a team allowing 5.6 per game). The Pirates had slightly more shutouts and one run allowed games than you’d expect given their overall RA/G, but the they had many more two run games, which are games that a team with an average offensive in a 4.75 R/G environment (which is the league average after adjusting for the PIT park factor) should have won 82.0% of the time. They gave some of this advantage back by giving up three runs more often (still a good amount to allow with a .686 W%), but they also had more four run games (still a .543 W%). They allowed 5-9 runs less often then expected, and those are games that they would be expected to lose (especially 6+, as the expected W% drops from .409 when allowing five to .296 when allowin six).

I don’t have a good clean process for combining gOW% and gDW% into an overall gEW%; instead I use Pythagenpat math to convert the gOW% and gDW% into equivalent runs and runs allowed and calculate an EW% from those. This can be compared to EW% figured using Pythagenpat with the average runs scored and allowed for a similar comparison of teams with positive and negative differences between the two approaches:

Positive: MIL, BAL
Negative: OAK, BOS, LA

The table below has the various winning percentages for each team: