Hitting by Position, 2011

Offensive performance by position (and the closely related topic of positional adjustments) has always interested me, and so each year I like to examine the most recent season's totals. I believe that offensive positional averages can be an important tool for approximating the defensive value of each position, but they certainly are not a magic bullet and need to include more than one year of data if they are to be utilized in that capacity.

The first obvious thing to look at is the positional totals for 2011, with the data coming from Baseball-Reference.com. "MLB” is the overall total for MLB, which is not the same as the sum of all the positions here, as pinch-hitters and runners are not included in those. “POS” is the MLB totals minus the pitcher totals, yielding the composite performance by non-pitchers. “PADJ” is the position adjustment, which is the position RG divided by the position (non-pitcher) average. “LPADJ” is the long-term positional adjustment that I use, based on 1992-2001 data. The rows “79” and “3D” are the combined corner outfield and 1B/DH totals, respectively:



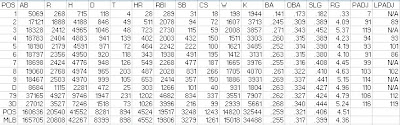
The 2011 results were most notable for the poor performance by third basemen and the pathetic effort by left fielders, who were slightly less productive than the average non-pitcher. After a down 2010, DHs rebounded to a respectable 110. The other positions were fairly close to their historical norms, and pitchers avoided setting a new all-time low, although the difference between 7 and 5 is negligible.

Speaking of pitchers, here are the aggregate park-adjusted totals for NL pitching teams. This analysis is based on simple ERP, and thus ignores sacrifices and the other situational goodness that makes pitcher hitting such an exciting and integral part of our national pastime:



Milwaukee ranked second and Arizona first last year, but on the other hand the Mets were third in 2010 and dead last in 2011. AL pitchers don’t get enough opportunities to bother with a chart, but for trivia’s sake, Baltimore’s pitchers raked .405/.405/.630, while Kansas City’s failed to reach base in eighteen plate appearances.

Moving on to positions that are actually expected to hit, I figured park-adjusted RAA for each position. The baseline for average is the overall 2011 MLB average RG for each position, with left and right field pooled. The leading team at each position was as follows (these are generally unsurprising so I’ll spare you a big chart):

C--DET, 1B--DET, 2B--BOS, 3B--CHN, SS--NYN, LF--MIL, CF--LA, RF--TOR, DH--BOS

The only one of these that was a bit surprising to me even after looking at the final stats for individuals was the Cubs’ third basemen (led of course by Aramis Ramirez). But a lot of the usual suspects at third base had injuries and other issues this year (Longoria, Zimmerman, Wright, Youkilis).

Now the worst performance at each position, along with a column displaying the team leader in games played at that spot:



It’s mostly a coincidence that all of the worst-hitting positions were from AL teams, although they do generally get more PA in which to drive down their RAA. I wrote about the Twins and Angels catchers a little in the previous post, but note here that Houston’s catchers were second last with -31 RAA and the Angels managed -29. The continuing inability of Seattle to generate offense is a marvel, and Juan Pierre is an appropriate banner carrier for 2011’s crop of poor hitting left fielders.

The following charts give the RAA at each position for each team, split up by division. The charts are sorted by the sum of RAA for the listed positions. As mentioned earlier, the league totals will not sum to zero since the overall ML average is being used and not the specific league average. Positions with negative RAA are in red; positions with +/- 20 RAA are bolded:



Third base and shortstop led the Mets to the highest infield RAA in the NL. Atlanta tied for the lowest outfield RAA in the NL. There must be something wrong with my spreadsheet as surely the Phillies first basemen combined for more than 8 RAA, led by their perennial MVP candidate.



St. Louis was the only team in the game to be above average at every position, and really stood at out at the three biggest offensive positions. Their outfield combined to lead MLB in RAA. Milwaukee’s offense was structured similarly, although right field did not stand out and they gave a lot of it back with a black hole at third base. The Cubs’ outfield production was evenly distributed and combined to tie Atlanta for the lowest mark in the NL. Pittsburgh’s infield tied for the NL’s trailer spot. Houston got decent production in the outfield but nowhere else.



The fact that the Los Angeles infield tied for the fewest RAA in the NL and yet the offense combined to lead the division should give you a quick idea on the offensive character of the NL West. While the World Series title makes it easy for some to overlook, San Francisco’s offensive struggles are persistent and pitching can only take you so far.



Boston’s offense was terrific despite right field, leading the majors in infield RAA. Toronto pulled a neat trick by combining for -17 RAA from the outfield despite having Jose Bautista.



Kansas City led the AL in outfield RAA, which not many would have predicted from Alex Gordon, Melky Cabrera, and Jeff Francoeur. Cleveland’s outfield was second-worst in the majors, and under normal circumstances -62 from the outfield would stick out more. The best thing that can be said about Chicago’s -98 RAA is that it was balanced -49/-49 between infield and outfield, with catcher and DH nearly average (+2/-2).



Texas kept the AL West from looking like it’s NL counterparts. Chris Iannetta and some guy whose name I can’t remember should do wonders for LAA. Oakland’s -50 runs from the infield was the worst in the majors, almost all driven by dreadful production at first base. And then there’s Seattle. What can one say about Seattle? Every outfield position was at least -20 (only five other outfield spots across the other 29 teams were at -20). Catcher, third base, and DH also stood out for the hapless Mariners.

Earlier I displayed some long-term positional adjustments that I’ve used over the years. It dawned on me in September that those were based on the ten-year period from 1992-2001, and that at this point, none of the most recent ten years are included in the sample. So I figured it would be an opportune time to recalibrate my position adjustments, using the ten years from 2002-2011 as the basis.

I figured two sets of PADJs; one which compared each position to the overall league average (including pitchers), and one that compared it to the league average less pitchers. There is very little difference, of course--the ones compared to the average including pitchers tend to be one or two points higher. This table compares the 1992-2001 and the 2002-2011 adjustments:



The big movers relative to 1992-2001 were the middle infield positions, improving offensively as first base/DH declined a little. In the end, though, the defensive spectrum one would draw based on offense doesn’t change at all, except for third base switching places with center field (and the differences were miniscule in both decades) to match Bill James’ spectrum.

A longer digression about the application of position adjustments, and some reasons why one might want to consider using offensive adjustments, will have to wait for another time, but would be appropriate here.

This spreadsheet includes the 2011 data by position.

Hitting by Lineup Slot, 2011

I devoted a whole post to leadoff hitters, whether justified or not, so it's only fair to have a post about hitting by batting order position in general. I certainly consider this piece to be more trivia than sabermetrics, since there’s no analytical content.

The data in this post was taken from Baseball-Reference. The figures for each team's runs are not park-adjusted--I intended to do so, but unfortunately I had already written the body of the post before I realized that they’d been omitted. The Padres having the worst 2, 3, and 4 production in the NL should have alerted me to this sooner. Then I had to go back and remove some comments that make no sense when ignoring park effects, so now the post is just a skeleton. Oh well. RC is ERP, including SB and CS, as used in my end of season stat posts. The weights used are constant across lineup positions; there was no attempt to apply specific weights to each position, although they are out there and would certainly make this a little bit more interesting.



This marks a third straight season that the most productive lineup slot in the majors was the NL’s #3 hitters…Pujols, Votto, Braun and company. Despite all of the seemingly silly things managers do with their batting orders, it is comforting to know that, from the cleanup spot down, each subsequent spot is less productive. Of course, that doesn’t excuse the feeble performance of NL #2 hitters, who just edged out the #8 hitters as the least productive NL spot filled by real hitters.

Next, here are the team leaders in RG at each lineup position. The player listed is the one who appeared in the most games in that spot (which can be misleading as the presence of Mitch Moreland demonstrates):



Houston actually had the NL’s most productive hitters at two spots; of course, they were two bottom of the batting order spots in which nobody contributes anyway. The least productive lineup spots:



As you can see, Minnesota had the worst production out of both the #8 and #9 spots. What makes this truly impressive, though, is that Drew Butera was the leader in games played in both spots. One thing I had meant to include in my meanderings post but forgot was a comparison of Mathis and Butera’s basic batting lines as I present them in my end of season stats. Neither had enough PA to qualify for those lists, but their seasons were too bad to just ignore:



Mathis was intentionally walked twice; both came in a June 17 game at the Mets. No word on whether or not Ron Washington temporarily replaced Terry Collins.

Note that Houston’s #9 hitters (the best in the NL at 2.3 RG) almost managed to outhit their #8 hitters (worst in the NL at 2.5 RG).

The next chart displays the top ten positions in terms of RAA, compared to their league’s average for each spot. A lot of the same suspects pop up, of course:



And the ten worst positions:



Finally, this table has each team’s RG rank among the lineup slots in their league. The top and bottom three in each league have been noted, which make Boston and Seattle stand out (for opposite reasons, of course).





Here is a link to a Google spreadsheet with the underlying data. The RG and RAA figures in this one are park-adjusted as should have been done throughout this post.

2011 Leadoff Hitters

This post kicks off a series of posts that I write every year, and therefore struggle to infuse with any sort of new perspective. However, they're a tradition on this blog and hold some general interest, so away we go.

This post looks at the offensive performance of teams' leadoff batters. I will try to make this as clear as possible: the statistics are based on the players that hit in the #1 slot in the batting order, whether they were actually leading off an inning or not. It includes the performance of all players who batted in that spot, including substitutes like pinch-hitters.

Listed in parentheses after a team are all players that appeared in twenty or more games in the leadoff slot--while you may see a listing like "BOS (Ellsbury)” this does not mean that the statistic is only based solely on Ellsbury's performance; it is the total of all Boston batters in the #1 spot, of which Ellsbury was the only one to appear in that spot in twenty or more games. I will list the top and bottom three teams in each category (plus the top/bottom team from each league if they don't make the ML top/bottom three); complete data is available in a spreadsheet linked at the end of the article. There are also no park factors applied anywhere in this article.

That's as clear as I can make it, and I hope it will suffice. I always feel obligated to point out that as a sabermetrician, I think that the importance of the batting order is often overstated, and that the best leadoff hitters would generally be the best cleanup hitters, the best #9 hitters, etc. However, since the leadoff spot gets a lot of attention, and teams pay particular attention to the spot, it is instructive to look at how each team fared there.

The conventional wisdom is that the primary job of the leadoff hitter is to get on base, and most simply, score runs. So let's start by looking at runs scored per 25.5 outs (AB - H + CS):

1. TEX (Kinsler), 6.8
2. MIL (Weeks/Hart), 6.5
3. BOS (Ellsbury), 6.4
Leadoff average, 5.0
ML average, 4.3
28. LAA (Izturis/Aybar), 4.0
29. STL (Theriot/Furcal), 3.9
30. WAS (Bernadina/Desmond/Espinosa), 3.9

Obviously you all know the biases inherent in looking at actual runs scored. It is odd to see St. Louis near the bottom as they had a good offense overall. Usually the leadoff hitters will manage to score some runs when they have Pujols, Holliday and Berkman coming up behind them whether they get on base that much or not.

Speaking of getting on base, the other obvious measure to look at is On Base Average. The figures here exclude HB and SF to be directly comparable to earlier versions of this article, but those categories are available in the spreadsheet if you'd like to include them:

1. CHN (Castro/Fukudome), .364
2. NYN (Reyes/Pagan), .364
3. BOS (Ellsbury), .362
Leadoff average, .324
ML average, .317
28. BAL (Hardy/Roberts/Andino), .287
29. SF (Torres/Rowand), .282
30. WAS (Bernadina/Desmond/Espinosa), .277

I would not have correctly identified the Cubs as having the highest OBA out of the leadoff spot in my first fifteen guesses, I don’t think. The seven point difference between the overall major league OBA and the OBA of leadoff men is a little smaller than it usually is, but last year the gap was just two points.

The next statistic is what I call Runners On Base Average. The genesis of it is from the A factor of Base Runs. It measures the number of times a batter reaches base per PA--excluding homers, since a batter that hits a home run never actually runs the bases. It also subtracts caught stealing here because the BsR version I often use does as well, but BsR versions based on initial baserunners rather than final baserunners do not.

My 2009 leadoff post was linked to a Cardinals message board, and this metric was the cause of a lot of confusion (this was mostly because the poster in question was thick-headed as could be, but it's still worth addressing). ROBA, like several other methods that follow, is not really a quality metric, it is a descriptive metric. A high ROBA is a good thing, but it's not necessarily better than a slightly lower ROBA plus a higher home run rate (which would produce a higher OBA and more runs). Listing ROBA is not in any way, shape or form a statement that hitting home runs is bad for a leadoff hitter. It is simply a recognition of the fact that a batter that hits a home run is not a baserunner. Base Runs is an excellent model of offense and ROBA is one of its components, and thus it holds some interest in describing how a team scored its runs, rather than how many it scored:

1. CHN (Castro/Fukudome), .339
2. NYN (Reyes/Pagan), .336
3. PIT (Tabata/McCutchen/Presley), .315
Leadoff average, .291
ML average, .285
28. SF (Torres/Rowand), .253
29. BAL (Hardy/Roberts/Andino), .253
30. WAS (Bernadina/Desmond/Espinosa), .247

You are probably starting to notice a lot of repetition in the leaders and trailers. Obviously a lot of these metrics measure the same thing in slightly different ways or measure similar things, so it’s to be expected.

I will also include what I've called Literal OBA here--this is just ROBA with HR subtracted from the denominator so that a homer does not lower LOBA, it simply has no effect. You don't really need ROBA and LOBA (or either, for that matter), but this might save some poor message board out there twenty posts, so here goes. LOBA = (H + W - HR - CS)/(AB + W - HR):

1. CHN (Castro/Fukudome), .344
2. NYN (Reyes/Pagan), .341
3. PIT (Tabata/McCutchen/Presley), .321
Leadoff average, .297
ML average, .292
28. BAL (Hardy/Roberts/Andino), .261
29. SF (Torres/Rowand), .257
30. WAS (Bernadina/Desmond/Espinosa), .252

In this presentation, the rank difference between ROBA and LOBA is barely noticeable.

The next two categories are most definitely categories of shape, not value. The first is the ratio of runs scored to RBI. Leadoff hitters as a group score many more runs than they drive in, partly due to their skills and partly due to lineup dynamics. Those with low ratios don’t fit the traditional leadoff profile as closely as those with high ratios (at least in the way their seasons played out):

1. LA (Gordon/Gwynn/Carroll/Furcal), 2.5
2. HOU (Bourn/Bourgeois/Schafer), 2.1
3. DET (Jackson), 2.0
Leadoff average, 1.6
26. WAS (Bernadina/Desmond/Espinosa), 1.2
28. KC (Gordon/Getz), 1.2
29. BOS (Ellsbury), 1.2
30. BAL (Hardy/Roberts/Andino), 1.2
ML average, 1.1

The presence of the Red Sox in the bottom three on this list should drive home the point about this not being a quality metric. The leadoff hitters that rank the lowest in R/BI are those that drive in almost as many runs as they score. If you had a leadoff hitter that was driving in many more runs than he scored, that might be cause for some reconsideration of your batting order, but having some scored/batted in parity is not inherently a bad thing.

A similar gauge, but one that doesn't rely on the teammate-dependent R and RBI totals, is Bill James' Run Element Ratio. RER was described by James as the ratio between those things that were especially helpful at the beginning of an inning (walks and stolen bases) to those that were especially helpful at the end of an inning (extra bases). It is a ratio of "setup" events to "cleanup" events. Singles aren't included because they often function in both roles.

Of course, there are RBI walks and doubles are a great way to start an inning, but RER classifies events based on when they have the highest relative value, at least from a simple analysis:

1. CHA (Pierre), 2.4
2. MIN (Revere/Span), 1.9
3. LA (Gordon/Gwynn/Carroll/Furcal), 1.8
Leadoff average, 1.0
ML average, .8
28. BAL (Hardy/Roberts/Andino), .6
29. BOS (Ellsbury), .6
30. MIL (Weeks/Hart), .6

Last year, the White Sox led handily in RER, due in large part to Pierre’s steals. This year, Pierre didn’t steal as many bases but still managed to slap his team to the top.

Speaking of stolen bases, last year I started including a measure that considered only base stealing. Obviously there's a lot more that goes into being a leadoff hitter than simply stealing bases, but it is one of the areas that is often cited as important. So I've included the ranking for what some analysts call net steals, SB - 2*CS. I'm not going to worry about the precise breakeven rate, which is probably closer to 75% than 67%, but is also variable based on situation. The ML and leadoff averages in this case are per team lineup slot:

1. HOU (Bourn/Bourgeois/Schafer), 29
1. NYN (Reyes/Pagan), 29
3. SEA (Suzuki), 26
Leadoff average, 11
ML average, 3
28. CHA (Pierre), -3
29. STL (Theriot/Furcal), -6
29. CLE (Brantley/Sizemore/Carrera), -6

The Indians have been just missed the trailer spots on a number of these lists. At least Cleveland and St. Louis are at the bottom largely because their leadoff hitters didn’t attempt that many steals. Only Milwaukee and Baltimore leadoff hitters (16 and 21 respectively) attempted fewer steals than Cleveland (24) and St. Louis (18). Neither the Tribe (58%) nor the Redbirds (56%) had success when they did steal, but they weren’t trying it all that much. The White Sox, on the other hand, were 31-48 (65%), a poor percentage and the eleventh-most attempts.

Let's shift gears back to quality measures, beginning with one that David Smyth proposed when I first wrote this annual leadoff review. Since the optimal weight for OBA in a x*OBA + SLG metric is generally something like 1.7, David suggested figuring 2*OBA + SLG for leadoff hitters, as a way to give a little extra boost to OBA while not distorting things too much, or even suffering an accuracy decline from standard OPS. Since this is a unitless measure anyway, I multiply it by .7 to approximate the standard OPS scale and call it 2OPS:

1. BOS (Ellsbury), 882
2. NYN (Reyes/Pagan), 835
3. MIL (Weeks/Hart), 834
Leadoff average, 733
ML average, 723
28. CHA (Pierre), 669
29. SF (Torres/Rowand), 645
30. WAS (Bernadina/Desmond/Espinosa), 630

Along the same lines, one can also evaluate leadoff hitters in the same way I'd go about evaluating any hitter, and just use Runs Created per Game with standard weights (this will include SB and CS, which are ignored by 2OPS):

1. BOS (Ellsbury), 6.7
2. NYN (Reyes/Pagan), 6.2
3. TEX (Kinsler), 6.1
Leadoff average, 4.6
ML average, 4.4
28. CHA (Pierre), 3.4
29. SF (Torres/Rowand), 3.4
30. WAS (Bernadina/Desmond/Espinosa), 3.4

Finally, allow me to close with a crude theoretical measure of linear weights supposing that the player always led off an inning (that is, batted in the bases empty, no outs state). There are weights out there (see The Book) for the leadoff slot in its average situation, but this variation is much easier to calculate (although also based on a silly and impossible premise).

The weights I used were based on the 2010 run expectancy table from Baseball Prospectus. Ideally I would have used multiple seasons but this is a seat-of-the-pants metric. Last year’s post went into the detail of how I figured it; this year, I’ll just tell you that the out coefficient was -.22, the CS coefficient was -.587, and for other details refer you to that post. I then restate it per the number of PA for an average leadoff spot (741 in 2011):

1. BOS (Ellsbury), 29
2. TEX (Kinsler), 26
3. NYN (Reyes/Pagan), 25
Leadoff average, 0
ML average, -3
28. CHA (Pierre), -20
29. WAS (Bernadina/Desmond/Espinosa), -20
30. SF (Torres/Rowand), -21

From an overview of all of these metrics, I think it’s safe to say that Red Sox and Mets leadoff hitters were pretty effective while White Sox, Nationals and Giants were not. I was a little disappointed that the Braves and Astros didn’t make any lists together here as each team used both Michael Bourn and Jordan Schafer in twenty or more games out of the #1 spot. Obviously that’s a possibility when players are traded for each other, but it would have been particularly amusing had one team been on the leader list and the other on the trailer list.

A spreadsheet with all of the data and the full lists is available.

Statistical Meanderings 2011

I have to apologize in advance for this--it sort of resembles a bad Jayson Stark piece with better metrics but less interesting tidbits.

* The discrepancy in R/G between the AL and NL (for the offenses) expanded to .33 (4.46 to 4.13) after a one-year blip that saw the two circuits only .12 runs apart. The leagues were equal in walk rate (.090 and .091 per at bat), but the AL hit for a higher BA (.258 to .253) and with more power (.150 to .139 ISO).

* I certainly do not intend to dispute the notion that Houston was the worst team in baseball, but Minnesota actually had a lower EW% and PW%. Based on runs and runs allowed, Houston “should have” won 61.8 games to Minnesota’s 61.5, and runs created expected a wider gap, 63.3 to 59.8. Obviously this does not consider strength of schedule, but it does put into perspective just how disastrous the Twins’ season was.

* Tampa Bay led the majors in converting balls in plays into outs by a wide margin; their DER of .712 was as far ahead of second place LAA as the Angeles were ahead of twentieth place STL. The Rays also led the majors in modified fielding average, albeit not by a runaway margin.

As a brief aside, “modified” fielding average is no more complex or accurate than regular old fielding average, except I remove strikeouts and assists from the formula. It would actually be easier to work with if I looked at the complement (errors/(putouts less strikeouts + errors)), but fielding average has been expressed that way for ever and it’s not a particularly telling metric in any event.

* In 2010, major league teams had an unusually high W% at home (.559) and 28 teams had a higher W% at home than on the road. This led to some speculation about whether there was something afoot.

2011 did not provide any such conspiracy fodder. Home teams had an abnormally low W% (.526), and only 23/30 teams (77%) won with a greater frequency at home. It was the lowest HW% for MLB since 2001 (.524), and 2005 was the last time that only 23 teams were better at home (only 20 were in 2001).

* The Giants scored 2.91 runs per game at home, the lowest output since 1972. They had to do the near impossible to achieve this by scoring less than the legendary 2010 Mariners (2.95). Offensive ineptitude combined with their good defense resulted in San Francisco playing in the lowest overall scoring context (7.09 RPG) in the majors since the 2003 Dodgers (6.98).

* Don’t tell anyone, but the two teams that struck out the fewest times were the Rangers (930) and the Cardinals (978). Both did unsurprisingly ground into a lot of double plays--Texas was sixth in MLB with 135 and St. Louis’ 169 was sixteen more than second place Baltimore.

* I always like to run a chart showing each playoff team’s RAA broken down by offense and defense:



As you can see, the average playoff team was fairly balanced. The only subpar unit in the group was the defense of the World Champion St. Louis Cardinals.

* At first glance, there was nothing remarkable about the Kansas City bullpen:



Their 4.26 relief eRA was equal to the American League average. But the interesting thing is that all of them were rookies except for Joakim Soria. I’ve already said nice things about Greg Holland in my Rookie of the Year post, so I won’t repeat that here.

* Someone beat me to it, but it is worth pointing out how low Trever Miller’s innings to appearance ratio was, particularly during his time in St. Louis. Miller recorded 47 outs in 39 appearances (1.21 O/G) with the Cards. I cannot state this absolutely, but I believe that is the lowest ratio in ML history for a pitcher with 20 or more appearances. The previous low I can find is Randy Flores with the 2009 Rockies (36 outs/27 games, 1.33). Miller’s complete season line was a yeoman 64 outs in 48 games, tying Flores’ record. A fitting achievement for Tony LaRussa’s final season if I may say so myself.

* One of the stats I track for relievers is inherited runners/game. In an era where leverage index is readily available, it doesn’t yield much marginal value, but I always like looking at closer usage through IR/G. Closers usually dominate the bottom of the IR/G list (I believe Mariano Rivera led full-time AL closers at .31, which was 71st out of 85 relievers), but it’s always fun to see which closers were never brought in with runners on base. If a manager never calls on his closer with runners on, he’s either really locked into bullpen roles, or he really doesn’t trust him. I’d assume the latter was the case with Kevin Gregg, who inherited zero runners in 2011. The former was the case for John Axford (1 in 74 appearances).

* Brian Wilson has taught us that a quirky personality, a ridiculous beard, and a World Series ring can get you a lot of commercials with 7 RAR. Who was the last closer so marginal that got so much publicity?

* Which Yankee reliever is which?



The point here is not to compare the two, but to point out that David Robertson had a really great season.

* You wouldn’t know it from watching the playoffs (and Ron Washington and the Rangers reluctance to use him that eventually turned into an outright dropping off of the roster), but Koji Uehara ranked fifth in RAR among AL relievers and was seventeenth last year. Of course, if all you went by was Washington’s managing, you would be shocked to learn where Nick Punto tends to rank on RAR lists.

* Five major league starters averaged 110 or more pitches per start this year, which has to be the most in some time. I’m pretty sure that hasn’t happened since I’ve been including P/S in my year end stat reports, although I didn’t go back and check to make sure. The five were: Verlander (117), Weaver (113), Halladay (111), Shields (111) and Sabathia (110).

* At the risk of cherry picking (as I’m sure I’m leaving out some pitchers that were talked about similarly but have had continued success, plus one season is obviously insufficient to draw conclusions in any event), I always find it a little satisfying when pitchers that were said to be DIPS beaters have either terrible or high BABIP seasons. Trevor Cahill is in the latter category--he wasn’t horrible by any means, and a .306 BABIP is not that high, but it still is not the kind of season a good DIPS beater should have. JA Happ, on the other hand, was atrocious and gave up an identical .306 BABIP. Even Charlie Morton sort of fits--even looking at his entire season, he wound up at -3 RAA with a .323 BABIP. Along those lines, what are the odds that Josh Tomlin is in the major leagues in five years? They can’t be that good.

* JoJo Reyes seemed to get a lot of attention for his lengthy (by time, especially) losing streak early in the year. Or perhaps my impression of that is off, magnified by the fact that I watched him get his first win pitching against Cleveland. In any event, Reyes may have had some bad luck along the way, but a lot of it evened out in 2011. A pitcher with a 6.45 RRA, 6.24 eRA and 5.21 dRA should consider himself darn lucky to wind up 7-11.

* PSA: David Freese is 28 and ranked 6th in RG among NL third basemen. I overlooked it, but Chase Headley actually had a .393 OBA and created 6.1 runs per game, second to Pablo Sandoval among NL third baseman. So postseaon hardware aside, Padres fans shouldn’t feel too terribly about which of their possible third basemen they actually have.

* AL players with negative RAR who at one time were actually good included Vernon Wells, Magglio Ordonez, JD Drew, Justin Morenau, Alex Rios, Chone Figgins and Adam Dunn. Morneau went from first among AL first baseman in RG in his concussion-shortened 2010 to last in 2011.

* AL players who had an OBA greater than their SLG were: Ryan Sweeney, Chris Getz, JD Drew and Adam Dunn. But for as bad as Dunn’s season was, Chone Figgins’ was actually worse on a rate basis. Figgins only played in 81 games to Dunn’s 122, but still held just a -15 to -17 RAR lead. Figgins created 1.75 runs per game, lowest among all major league players with 300 PA, lower even than Paul Janish (1.90).

* Which of these teammates would you assume was more valuable, based on the statistics presented here?



Of course, any opinion you’d form would be woefully incomplete, because I’ve only given you offensive statistics, without telling you anything about position or defense. Offensively, though, they are nearly indistinguishable. So what if I tell you that one of these players is a slow first baseman and the other one is a center fielder? Surely, the center fielder must have been more valuable, right?

How about these two teammates?



They both play the same position, but one of them was signed as a free agent and took the other’s spot at their common position (third base)--so the one who was pushed off played 105 games at 1B/DH and 55 games at the other infield positions. The one who got the fielding job was more likely the more valuable player, right?

One would think. But the first baseman finished 10th in the MVP voting and the center fielder finished 13th. The third baseman finished fifteenth while the 1B/DH finished 8th and got a first place vote.

IBA Ballot: MVP

My position on pitchers as MVP candidates is pretty simple: I think they absolutely should be considered. However, that doesn’t mean it’s a common occurrence for me to conclude that a pitcher was the MVP of his league. In general, I think that given modern workloads, it is much more likely for a batter to be the MVP than a pitcher. Additionally, when I conclude that a pitcher and a position player are indistinguishable in terms of value, I will usually hedge my bets and go with the batter. A corollary to this is that I’d like the pitcher’s peripheral statistics to indicate that he is equally or more valuable than his batting rivals, not just his actual runs allowed. This is a higher hurdle to clear, since the best pitchers in terms of runs allowed are more likely than not to have outpitched their peripherals.

The end result of this thinking is that somewhere around 2-4 pitchers are sprinkled through my MVP ballot, but rarely is one listed at #1. I’ve been formally writing up my ballots for this blog since 2006, which gives me ten league-seasons with which to quantify my thought process:



As you can see, on average I list three pitchers on my ballot, with the leading pitcher placed fourth. Obviously I’m biased, but I think this is a very fair treatment of pitchers.

All of this bloviating and laughably in-depth analysis of my own previous ballots is necessary because, for the first time since I’ve been doing this, there is a popular movement to vote a starting pitcher as MVP. I want to make it clear that, and I think I have, that if I don’t feel that Justin Verlander was the AL MVP, it’s not because of some bias against pitchers, but simply that I felt other player(s) were more valuable in 2011.

Verlander has gained traction as a candidate for two reasons. One, he pitched for a playoff team, and heavens knows that mainstream types will bend over backwards to try to give the MVP to a player whose contributions were “actually valuable”, or whatever argument they’d like to use to dismiss players whose teammates just weren’t that good. It also helps that of the AL playoff teams, Detroit was something of a surprise (they were certainly the most surprising to me, although the voters would probably give that nod to Tampa Bay), and they made a strong surge in August and September to run away with their division. That’s a good narrative.

Secondly, Verlander’s W-L record is very impressive (24-5), and we all know that the mainstream still is easily distracted by a shiny W-L record. And oh yeah, third, he pitched very well by any measure.

That last point, though, is where I’m not as enthusiastic about Verlander. The mainstream view is that Verlander was obviously the AL’s best pitcher in 2011--my view is that he was a solid #1, but Jered Weaver can’t just be laughed off. Verlander’s season is not historic by any means when viewed through the lens of RAR--for last five seasons, the AL pitching RAR leaders totals have been:

72, 84, 95, 76, 84

Verlander’s 84 is very good, but the average of the previous four AL leaders was 82. It’s a fairly typical league-leading type of performance, a very solid Cy Young-type season, but not one for the ages either.

However, I have Jose Bautista at 82 RAR/63 RAA, I don’t see any compelling reason to penalize him for his defense or baserunning (UZR doesn’t think much of him, but Dewan’s DRS and Wyers’ FRAA don’t share that evaluation), and I don’t care that his team finished in fourth place. Verlander does not look nearly as good when evaluated by dRA, and so when there’s reasonable doubt that the pitcher was more valuable than the position player, I side with the position player.

I also have placed Verlander’s teammate Miguel Cabrera ahead of him, albeit with much less conviction. Cabrera’s offensive value is essentially indistinguishable from Bautista’s--I estimate that Cabrera created 137 runs in 376 outs while Bautista created 134 runs in 363 outs (9.3 to 9.4 RG, 71 to 70 HRAA). However, Cabrera played first base and there’s reason to believe he’s a below-average fielder, putting Bautista ahead. Compared to Verlander, though, I think the case can be made that he was a little more valuable.

Among the other position player candidates to fill out the ballots, Jacoby Ellsbury ranks first in RAR, plus fielding and baserunning would seem to work in his favor. Adrian Gonzalez was right behind his teammate in RAR, and has a good fielding reputation and a decent showing in fielding metrics.

The other three spots all go to second baseman. I suppose one can argue that the positional adjustments I use are too kind to second basemen, but I just happen to think there is a collection of very talented second basemen in the AL at this time. Dustin Pedroia was just behind Ellsbury and Gonzalez in RAR. Curtis Granderson (56 RAR) and Mike Napoli (56) rank ahead of the trio of Robinson Cano (53), Ben Zobrist (52), and Ian Kinsler (50), but Granderson’s fielding raises at least a little concern. Napoli’s RAR gives him a full catcher position adjustment, but he actually played nearly as many games between first base and DH (53) as he did as a catcher (61). While his 8.5 RG ranked third in the AL behind Bautista and Cabrera, he also logged just 427 PA.

Among the three remaining second basemen, the offensive differences are small enough to throw a bone to Kinsler’s well-regarded fielding (at least by the various metrics)and baserunning, while keeping in mind that Zobrist like Napoli also played a fair amount at less demanding positions. Evan Longoria will probably get a lot more love from others, but he ranks 16th on my RAR list and would require more fielding credit than I am comfortable with (or a repudiation of the position adjustment for 3B relative to 2B) to make the ballot:

1) RF Jose Bautista, TOR
2) 1B Miguel Cabrera, DET
3) SP Justin Verlander, DET
4) SP Jered Weaver, LAA
5) CF Jacoby Ellsbury, BOS
6) 1B Adrian Gonzalez, BOS
7) 2B Dustin Pedroia, BOS
8) SP James Shields, TB
9) SP CC Sabathia, NYA
10) 2B Ian Kinsler, TEX

In the National League, there is no need for philosophical reflection about the value of a pitcher versus a position player, or any need for intricate comparisons of multiple players. There is only one question that needs to be answered: Can you make a case against Matt Kemp?

Kemp led NL hitters in RAR by 12, and was in a tied Ryan Bruan for the league lead with a 8.5 RG. His fielding is probably not great, but since no one else was particular close in RAR, you’d have to think he was pretty bad and that Ryan Braun or Prince Fielder or Jose Reyes was really good in the field to close the gap. I don’t see any reason to believe that, so Kemp is my runaway choice as NL MVP.

Filling out the rest of the ballot, Ryan Braun is a very strong candidate for #2. The three pitchers (Halladay, Kershaw, and Lee) that were very close for the Cy Young are all strong mid-ballot choices. Prince Fielder was very good, but inferior to his teammate at the plate and he’s not a strong candidate for fielding and baserunning credit. Jose Reyes and Joey Votto are also in the mix.

As you can see, I’m having trouble finding much to say about the NL ballot. My RAR list actually makes it pretty straightforward; obviously small differences are not meaningful, but I don’t see a lot of compelling reasons to step in and make changes. The only player who drops far below his RAR is Lance Berkman, who obviously is not much of a fielder at this point and who I would be loathe to argue was more valuable than teammate Pujols. And that leaves him without a spot:

1) CF Matt Kemp, LA
2) LF Ryan Braun, MIL
3) SP Roy Halladay, PHI
4) 1B Prince Fielder, MIL
5) SS Jose Reyes, NYN
6) 1B Joey Votto, CIN
7) SP Clayton Kershaw, LA
8) SP Cliff Lee, PHI
9) 1B Albert Pujols, STL
10) SS Troy Tulowitzki, COL

IBA Ballot: Cy Young

In retroactively evaluating starting pitchers, I start with their actual runs allowed (crudely adjusted for bequeathed runners to produce what I call RRA). I consider peripherals, primarily what I call eRA (basically a component RA) and dRA (a DIPS RA). However, I do not start with either of those, and if there is a substantial difference in RRA, I usually don’t override it lightly. I’m not sure that this stance makes much of a difference in this year’s Cy Young vote, at least at the top of the ballot--the top guys fare well however you slice it, but it does put me at odds with anyone following what could be called the Fangraphs school of pitcher evaluation.

Everyone has handed the AL Cy Young to Justin Verlander, but consider this:



I don’t think that, looking at these categories, you can come to any sort of clear conclusion about who was the better pitcher. The first guy pitched sixteen more innings, but he allowed .15 more runs per game, so when you compare them to a baseline, they are just about even. The first pitcher had a better eRA, which is a positive, but the second pitcher didn’t grossly outpitch his peripherals. All things outside of this chart being equal, I’d give the edge to the first pitcher, but I would hardly consider it a landslide.

As you probably know, the first pitcher is Justin Verlander; the second pitcher is Jered Weaver. Weaver also trailed Verlander in dRA (3.44 to 3.75), which I purposely omitted in order to make a point, and obviously Verlander has the win-loss angle going for him in the mainstream. I have no qualms about putting Verlander first on my ballot, but Weaver ensured that he didn’t run away from the rest of the AL field.

James Shields has a fairly large lead for the third spot on the RAR list at 77, with Sababthia fourth at 66 and three pitchers tightly clustered just below (Romero 62, Haren 62, Beckett 61). Shields and Romero both benefitted from low BABIPs (.259 and .247). Shields’ Rays teammates did lead the majors in DER by a wide margin; it wasn’t just him who was getting great defensive support. Still, as discussed above, given Shields’ sizeable RAR lead over the others, I’m more comfortable giving him the nod. It is enough to drop Romero out of the running for the last spot on the ballot, which comes down to Haren and Beckett.

Haren worked 45 more innings, but Beckett’s RRA was .51 runs lower and his eRA was .42 runs lower. However, Haren’s dRA was .24 runs lower, and since the peripherals are a split decision, I’m more comfortable going with the guy who worked a lot more. Fried chicken was not a factor in this decision:

1) Justin Verlander, DET
2) Jered Weaver, LAA
3) James Shields, TB
4) CC Sabathia, NYA
5) Dan Haren, LAA

The NL Cy Young is very close. Consider these two pitchers:



It would be tough to get much closer than that, wouldn’t it? While it appears that Clayton Kershaw will win the award and that Roy Halladay is the consensus #2, the top line on that table is Kershaw and the second line is Cliff Lee. Lee’s season is nearly indistinguishable from Kershaw’s in the categories that drive my decision. Halladay’s same categories line: 234, 2.48, 2.70, 2.71, 43, 73.

This race is close enough that I decided to take a look at each pitcher’s performance on a game-by-game basis, using the relatively crude gW% I discussed in this post. However, looking at each game on its own does little more than verify that these pitchers were all very close: Lee leads the way at .685, but Halladay at .680 and Kershaw at .679 are right behind.

We could consider strength of schedule. On the team level, and considering just the opponent’s overall quality rather than isolating opposing offense as would be more useful for comparing pitchers, my crude team rankings indicate that PHI and LA played nearly the same caliber of opposition--PHI has a 95 SOS and LA a 94. Baseball Prospectus’ data on quality of opposing hitter reveals that Halladay’s average opponent hit .260/.330/.413, Kershaw’s .263/.327/.416, and Lee’s .266/.332/.423. Respectively, those lines translate to approximate runs/game of 4.69, 4.67, and 4.83. But over 233 innings, even the difference between the high (Lee, 4.83) and the low (Kershaw, 4.67) is just 4 runs, and those figures probably shouldn’t be applied without any sort of regression.

From the game-by-game analysis, I can also compute the pitcher’s personal park factor weighted by innings pitched in each park rather than assuming that each pitcher logged a 50/50 home/road innings split. My standard park factor for PHI is 101 versus 97 for LA. Halladay and Lee’s personal park factors are both 101, while Kershaw’s is 96, making any sort of deviation from just using the team PFs an exercise in futility.

I put next to zero stock in win-loss record, but Kershaw’s is 21-5 mark is obviously more impressive than Halladay’s 19-6 and Lee’s 17-8 when compared to their team’s winning percentage. The pitcher’s run support (from ESPN.com) were 5.89, 5.52, and 4.95 respectively, which helps explain why Lee’s record lags behind the other two, but does next to nothing to help us sort out how effective they all were.

In the end, I give the nod to Halladay--he led the three pitchers in all three run averages, and he does have a 5 RAR lead. That doesn't prove he was better, but I have no reason to override it. I think that a reasonable person could easily conclude that Kershaw or Lee deserved the award as well.

For the other two spots on the ballot, the RAR list highly recommends Ian Kennedy (61 RAR) and Cole Hamels (59), as Tim Lincecum is sixth on the list a full eight runs behind Hamels. Hamels has slightly better peripherals than Kennedy, and while batted ball metrics are of questionable value, he does much better in those categories than Kennedy. In this case it confirms my default position (Hamels > Kennedy), and so I’ll give in and fill out my ballot as follows:

1) Roy Halladay, PHI
2) Clayton Kershaw, LA
3) Cliff Lee, PHI
4) Cole Hamels, PHI
5) Ian Kennedy, ARI

IBA Ballot: Rookie of the Year

I will admit up front that I have not paid much attention this year to the award debates, either in the mainstream or the sabersphere. This is good in the sense that I am coming into this cold, without having read many other perspectives that might bias me one way or another. It’s also bad for the same reason--while I don’t think I’ve ever found mainstream commentary on player value particularly useful, there are a lot of others out there worth reading.

I simply decided this year that I wasn’t going to waste any time thinking about awards until the season was over. Not that I ever obsessed over them previously, but I pretty much completely shut them out of my mind this year. So much so that when an acquaintance who knows I’m a baseball nut asked me who I thought should be the NL Cy Young winner a couple weeks ago, he was shocked when the best I could offer was “uh, probably either Halladay or Kershaw”.

In any event, let me start in the AL. This rookie crop belongs to the pitchers. My top three candidates are all starting pitchers. Michael Pineda got out the best start, Ivan Nova had the flashiest win-loss record, but Jeremy Hellickson was the AL’s most valuable rookie pitcher. Hellickson led the trio in innings (189 to Pineda’s 171 and Nova’s 165) and RRA (3.24 to 3.81 and 4.10). Combining the two, I have Hellickson at 52 RAR, Pineda 36, and Nova 30.

Hellickson’s BABIP was just .229, so from a strict DIPS perspective one could make a case for Pineda (or even Nova) ahead of Hellickson. But for a retrospective award, I stick to actual runs allowed and first-order component RA for the most part. If Pineda and Hellickson were close, I would consider moving the former ahead, but the gap is too big in this case.

For the remaining two spots on the ballot, the top position players are Dustin Ackley, Eric Hosmer, and Jemile Weeks. Ackley was the most productive hitter of the three, while Hosmer had 130 more PA than either of them. I have Ackley and Weeks both at 23 RAR with Hosmer at 21. Fielding and baserunning would seem to favor Weeks.

Greg Holland deserves a mention at least a mention as a reliever. Holland stranded 31 of 33 baserunners, the second-best performance of any AL reliever, and his peripherals were terrific as well. However, his 26 RAR is thanks in large part to the inherited runner performance, and thanks to Hosmer I wouldn’t be comfortable naming him the most valuable rookie on his own team. So I see it as:

1) SP Jeremy Hellickson, TB
2) SP Michael Pineda, SEA
3) SP Ivan Nova, NYA
4) 2B Jemile Weeks, OAK
5) 2B Dustin Ackley, SEA

You’ll note that I consider Mark Trumbo an afterthought. Yes, he hit 29 homers, but he also drew just 25 walks. His .290 OBA was second-lowest among AL first baseman with 300 PA, so despite the power, he ranks in the middle of the pack offensively at his position. He wouldn’t crack my top ten.

If Trumbo is the biggest source of divergence from my take on the award and the mainstream, his NL counterpart will certainly be Craig Kimbrel. Kimbrel was terrific by any measure, but in the end you have 77 innings pitched. I don’t believe in extreme leverage bonuses--or much of a leverage bonus at all. I’ll give him an arbitrary 25% boost to get to 25 RAR, but no more.

Among position players, the three standouts are Kimbrel’s teammate Freddie Freeman and Washington teammates Wilson Ramos and Danny Espinosa. I have them all essentially even in terms of RAR at 27. BP’s FRAA likes Espinosa’s fielding and baserunning, and that’s enough to put him in the lead. I suspect Freeman will get more support than Ramos, but the two aren’t that far apart as hitters, with Freeman creating 5.3 runs per game and Ramos 5.0. Freeman had nearly 200 more PA, but Ramos is a catcher. Freeman’s fielding reputation is good, but his FRAA was -5. It can go either way, but I prefer Ramos.

Josh Collmenter and Vance Worley were the top starters, with apologies to Cory Luebke, who I could certainly make a ballot case for, but will refrain lest I be accused of favoritism. Collmenter worked 23 more innings than Worley, which puts him 5 RAR ahead (36 to 31). Collmenter did have a BABIP of just .263 to Worley’s .293, but the dRA difference is not large enough (4.06 to 3.72) to convince me to put Worley ahead.

Depending on how you value Espinosa’s fielding, you certainly could conclude that he was more valuable than Collmenter--conservatively, I’ll stick with the later, and so my ballot is:
1) SP Josh Collmenter, ARI
2) 2B Danny Espinosa, WAS
3) SP Vance Worley, PHI
4) C Wilson Ramos, WAS
5) RP Craig Kimbrel, ATL

Baseball

It has been a part of my life for almost as long as I can remember and it will remain so for as long as I live. For seven months of the year, it is as familiar a part of my life as brushing my teeth or eating dinner, and so it is easy to take for granted. But then one day I wake up and suddenly it is gone, and in the void there is malaise. When the weather is nice, it is played; when it is dark and cold, it moves towards the tropics and away from focus. While it can be used to tell seasons, it scoffs at time while it is played. The competitors dictate the endpoint through their play.

It is a team game, but in many ways it allows the individual to stand and be judged on his own merits. It is a game that, through its variants and offshoots, is quite playable by a large number of people. It is the great American pastime, but it is also the great Cuban passion, the great Dominican pastime, perhaps the most popular import Japan has ever known. We call it baseball, but it is equally beisbol, yakyu, honkbal, pelota.

It is a game simple enough that it can be described (and recorded, on nothing more complex than a piece of paper) discretely--by inning, by score, by out, by baserunner, by count--yet complex enough that there are hundreds and hundreds of people like me who are fascinated by it and spend much of our free time thinking about it, yet we still discover new things about it.

And if you are wired to view the world in a certain way, to try to find and verify patterns, to quantify when possible, and sometimes to find meaning and order through randomness and chance--then sabermetrics is a vessel for enjoying it, understanding it, and celebrating it. To know that what we have seen over the last month is not just unlikely--but rather to have a systematic way of thinking that allows us to estimate just how unlikely--does not detract from it.

Once in a while we are presented with just one more game--one game that is, without question, the end. It almost goes against the spirit of the game to be pettily constrained by a set limit of games that cannot be cheated, unlike the nine innings that often become ten, and sometimes become twelve, and on glorious occasions become twenty, and in theory can be infinite. The potential is often greater than the payoff--but either way, the journey was incredible.

Brief Playoff Meanderings

* There have been eighteen postseasons in which the Division Series has been held (I’m counting the 1981 playoffs between the half-season winners as Division Series). 2011 set the new record for the most aggregate games played in the round, with nineteen. The maximum is twenty, and had the Rays managed to take an additional game from the Rangers it would have been reached. The previous high was eighteen, which occurred in 1981, 2001 and 2003.

The record for most total games played in the postseason (since 1995; in this case I’m excluding 1981 because the LCS was only a five-game series at that point) is 38 in 2003--two LDS went four and the World Series went six, but all other series went the distance. The ALCS and NLCS are both well-remembered (I can just say Grady Little or Aaron Boone and Steve Bartman and you’ll remember the circumstances).

No other postseason has come particularly close; the runner-up is 2001, which saw 35 total games played despite each LCS only lasting five games. The fewest games played in a post-season is 28 in 2007--every series was a sweep except for the two involving Cleveland, who beat New York in four in the ALDS then lost to Boston in seven in the ALCS. To put 2007 in perspective, every series from here on out in 2011 could be a sweep, and the total games played would be 31.

A natural follow-up question is “What is the expected number of postseason games?” If you assume that each game is a 50/50 proposition (equally matched teams, no home field advantage, no variation in team quality from day-to-day, etc.), then it’s very straightforward to estimate series length with the geometric distribution.

For a five-game series under those assumptions, there is a 25% chance for a sweep and a 37.5% chance for a four or five game series. For a seven-game series, there is a 12.5% chance for four games, 25% for five games, and 31.25% for six or seven games. Thus, the expected length of a five-game series is 4.125 games, the expected length of a seven-game series is 5.8125 games, and the expected number of games in the postseason is 33.9375. 1997, 2002 and 2004 all met expectations with 34 games.

However, if one compares the expected series lengths to the observed series length in the divisional era (1969 and foreward), he will find that five-game series do not conform to expectations:



Five-game series tend to be resolved in fewer games than one would expect assuming an equal probability of each outcome. The difference is statistically significant by reasonable standards. The average is just 3.86 games. Assuming that one of the teams has a .716 expected winning percentage comes close to minimizing the error assuming the geometric distribution framework:



I’m presenting this as a curiosity, and I’m certainly not suggesting that we should assume that the assumptions I described are useless when thinking about the Division Series. And on the other hand, seven-game series since 1969 conform almost as well as one could hope for:



There is a slight tendency for series to be resolved more quickly than one would expect, but it isn’t particularly significant, and the average of 5.75 is not far off the expected 5.81.

*What I’m going to say here is not in any way novel; many fans, both sabermetrically-inclined and not have expressed the same opinion over the years. But there were two instances that I considered so egregious in the Arizona/Milwaukee game give that I can’t help but comment on it here.

I have always thought that many managers are way too eager to make substitutions that sacrifice offense for baserunning or defense or the pitcher’s slot in the lineup, but I’m not sure I’ve ever seen a better display of it than in the aforementioned Game Five. In the eighth inning, Arizona trailed 2-1 with runners at first and third and two out. Chris Young drew a walk to load the bases and advance Miguel Montero from first to second, bringing Ryan Roberts up with the bases loaded.

At this point, Kirk Gibson decided to pinch-run for Montero, sending Collin Cowgill in. Montero occupied the #4 spot in the order, while Roberts was #7. Thus, it doesn’t take a rocket scientist to realize that, with an additional inning to go, there was a pretty good chance that Montero’s vacated spot would come up to bat again, and barring Arizona scoring at least two runs and holding Milwaukee in the bottom of the eighth, it would come with the Diamondbacks still needing a run (when I say needing a run, I mean it in the sense that Gibson apparently considered, since I would never say you don’t “need” more runs at any point in the game).

One would have to evaluate the marginal value of Cowgill’s baserunning very highly to see that as a winning move, especially considering that Montero would be off with contact given that their were two outs. Of course, as it played out, Roberts grounded into a fielder’s choice, and Montero’s spot did come up in the ninth, with the game now tied but runners at the corners and two outs. Henry Blanco hit into a fielder’s choice, and Arizona did not mount a threat in the tenth before allowing the game-winning run in the bottom of the frame.

The second move was not nearly as egregious, but it was still quite puzzling to me. With a 2-1 lead in the top of the ninth, Ron Roenicke summoned his closer, John Axford. The pitcher’s spot was due up fourth in the bottom of the ninth, so he double-switched Axford into Rickie Weeks’ #5 spot since he’d made the last out of the eighth.

Given that Roenicke wanted to make a double switch, Weeks was the only obvious candidate to be replaced--removing Braun or Fielder would be worse, especially since they were closer to coming to the plate, and Nyjer Morgan’s second spot was due up sixth in the bottom of the ninth. (One could make a case that Morgan would be the best candidate, but given that he got the walkoff hit in the tenth it wouldn’t be an argument that would fly over well with the “results not process” crowd).

What I find interesting about the double-switch for the home team taking the lead into the top of the ninth is that the only way the batting order matters at all is if Axford surrenders the lead. Thus, while you preserve Axford’s ability to pitch the tenth without sabotaging your offense in the ninth, you also know that if he does so, it will be only after he yielded a run in the ninth. You know that you will “need” runs if the #5 spot ever comes to the plate again.

Of course, this all worked out for Roenicke, since Axford pitched a 1-2-3 tenth, Morgan got the game-winning hit, and the #5 spot never batted again. And Roenicke does apparently like to bring Counsell in as a defensive replacement for Weeks, so if Weeks is going to come out of the game anyway, the double switch is the way to do it.

End of Season Statistics 2011

The spreadsheets are published as Google Spreadsheets, which you can download in Excel format by changing the extension in the address from "=html" to "=xls". That way you can download them and manipulate things however you see fit.

The data comes from a number of different sources. Most of the basic data comes from Doug's Stats, which is a very handy site. KJOK's park database provided some of the data used in the park factors, but for recent seasons park data comes from anywhere that has it--Doug's Stats, or Baseball-Reference, or ESPN.com, or MLB.com. Data on pitcher's batted ball types allowed, doubles/triples allowed, and inherited/bequeathed runners comes from Baseball Prospectus.

The basic philosophy behind these stats is to use the simplest methods that have acceptable accuracy. Of course, "acceptable" is in the eye of the beholder, namely me. I use Pythagenpat not because other run/win converters, like a constant RPW or a fixed exponent are not accurate enough for this purpose, but because it's mine and it would be kind of odd if I didn't use it.

If I seem to be a stickler for purity in my critiques of others' methods, I'd contend it is usually in a theoretical sense, not an input sense. So when I exclude hit batters, I'm not saying that hit batters are worthless or that they *should* be ignored; it's just easier not to mess with them and not that much less accurate.

I also don't really have a problem with people using sub-standard methods (say, Basic RC) as long as they acknowledge that they are sub-standard. If someone pretends that Basic RC doesn't undervalue walks or cause problems when applied to extreme individuals, I'll call them on it; if they explain its shortcomings but use it regardless, I accept that. Take these last three paragraphs as my acknowledgment that some of the statistics displayed here have shortcomings as well.

The League spreadsheet is pretty straightforward--it includes league totals and averages for a number of categories, most or all of which are explained at appropriate junctures throughout this piece. The advent of interleague play has created two different sets of league totals--one for the offense of league teams and one for the defense of league teams. Before interleague play, these two were identical. I do not present both sets of totals (you can figure the defensive ones yourself from the team spreadsheet, if you desire), just those for the offenses. The exception is for the defense-specific statistics, like innings pitched and quality starts. The figures for those categories in the league report are for the defenses of the league's teams. However, I do include each league's breakdown of basic pitching stats between starters and relievers (denoted by "s" or "r" prefixes), and so summing those will yield the totals from the pitching side. The one abbreviation you might not recognize is "N"--this is the league average of runs/game for one team, and it will pop up again.

The Team spreadsheet focuses on overall team performance--wins, losses, runs scored, runs allowed. The columns included are: Park Factor (PF), Home Run Park Factor (PFhr), Winning Percentage (W%), Expected W% (EW%), Predicted W% (PW%), wins, losses, runs, runs allowed, Runs Created (RC), Runs Created Allowed (RCA), Home Winning Percentage (HW%), Road Winning Percentage (RW%) [exactly what they sound like--W% at home and on the road], Runs/Game (R/G), Runs Allowed/Game (RA/G), Runs Created/Game (RCG), Runs Created Allowed/Game (RCAG), and Runs Per Game (the average number of runs scored an allowed per game). Ideally, I would use outs as the denominator, but for teams, outs and games are so closely related that I don’t think it’s worth the extra effort.

The runs and Runs Created figures are unadjusted, but the per-game averages are park-adjusted, except for RPG which is also raw. Runs Created and Runs Created Allowed are both based on a simple Base Runs formula. The formula is:

A = H + W - HR - CS
B = (2TB - H - 4HR + .05W + 1.5SB)*.76
C = AB - H
D = HR
Naturally, A*B/(B + C) + D.

I have explained the methodology used to figure the PFs before, but the cliff’s notes version is that they are based on five years of data when applicable, include both runs scored and allowed, and they are regressed towards average (PF = 1), with the amount of regression varying based on the number of years of data used. There are factors for both runs and home runs. The initial PF (not shown) is:

iPF = (H*T/(R*(T - 1) + H) + 1)/2
where H = RPG in home games, R = RPG in road games, T = # teams in league (14 for AL and 16 for NL). Then the iPF is converted to the PF by taking x*iPF + (1-x), where x = .6 if one year of data is used, .7 for 2, .8 for 3, and .9 for 4+.

It is important to note, since there always seems to be confusion about this, that these park factors already incorporate the fact that the average player plays 50% on the road and 50% at home. That is what the adding one and dividing by 2 in the iPF is all about. So if I list Fenway Park with a 1.02 PF, that means that it actually increases RPG by 4%.

In the calculation of the PFs, I did not get picky and take out “home” games that were actually at neutral sites, like the Astros/Cubs series that was moved to Milwaukee in 2008.

There are also Team Offense and Defense spreadsheets. These include the following categories:

Team offense: Plate Appearances, Batting Average (BA), On Base Average (OBA), Slugging Average (SLG), Secondary Average (SEC), Walks per At Bat (WAB), Isolated Power (SLG - BA), R/G at home (hR/G), and R/G on the road (rR/G) BA, OBA, SLG, WAB, and ISO are park-adjusted by dividing by the square root of park factor (or the equivalent; WAB = (OBA - BA)/(1 - OBA) and ISO = SLG - BA).

Team defense: Innings Pitched, BA, OBA, SLG, Innings per Start (IP/S), Starter's eRA (seRA), Reliever's eRA (reRA), RA/G at home (hRA/G), RA/G on the road (rRA/G), Battery Mishap Rate (BMR), Modified Fielding Average (mFA), and Defensive Efficiency Record (DER). BA, OBA, and SLG are park-adjusted by dividing by the square root of PF; seRA and reRA are divided by PF.

The three fielding metrics I've included are limited it only to metrics that a) I can calculate myself and b) are based on the basic available data, not specialized PBP data. The three metrics are explained in this post, but here are quick descriptions of each:

1) BMR--wild pitches and passed balls per 100 baserunners = (WP + PB)/(H + W - HR)*100

2) mFA--fielding average removing strikeouts and assists = (PO - K)/(PO - K + E)

3) DER--the Bill James classic, using only the PA-based estimate of plays made. Based on a suggestion by Terpsfan101, I've tweaked the error coefficient. Plays Made = PA - K - H - W - HR - HB - .64E and DER = PM/(PM + H - HR + .64E)

Next are the individual player reports. I defined a starting pitcher as one with 15 or more starts. All other pitchers are eligible to be included as a reliever. If a pitcher has 40 appearances, then they are included. Additionally, if a pitcher has 50 innings and less than 50% of his appearances are starts, he is also included as a reliever (this allows some swingmen type pitchers who wouldn’t meet either the minimum start or appearance standards to get in).

For all of the player reports, ages are based on simply subtracting their year of birth from 2011. I realize that this is not compatible with how ages are usually listed and so “Age 27” doesn’t necessarily correspond to age 27 as I list it, but it makes everything a heckuva lot easier, and I am more interested in comparing the ages of the players to their contemporaries, for which case it makes very little difference. The "R" category records rookie status with a "R" for rookies and a blank for everyone else; I've trusted Baseball Prospectus on this. Also, all players are counted as being on the team with whom they played/pitched (IP or PA as appropriate) the most.

For relievers, the categories listed are: Games, Innings Pitched, Run Average (RA), Relief Run Average (RRA), Earned Run Average (ERA), Estimated Run Average (eRA), DIPS Run Average (dRA), Batted Ball Run Average (cRA), SIERA-style Run Average (sRA), Guess-Future (G-F), Inherited Runners per Game (IR/G), Batting Average on Balls in Play (%H), Runs Above Average (RAA), and Runs Above Replacement (RAR).

IR/G is per relief appearance (G - GS); it is an interesting thing to look at, I think, in lieu of actual leverage data. You can see which closers come in with runners on base, and which are used nearly exclusively to start innings. Of course, you can’t infer too much; there are bad relievers who come in with a lot of people on base, not because they are being used in high leverage situations, but because they are long men being used in low-leverage situations already out of hand.

For starting pitchers, the columns are: Wins, Losses, Innings Pitched, RA, RRA, ERA, eRA, dRA, cRA, sRA, G-F, %H, Pitches/Start (P/S), Quality Start Percentage (QS%), RAA, and RAR. RA and ERA you know--R*9/IP or ER*9/IP, park-adjusted by dividing by PF. The formulas for eRA, dRA, cRA, and sRA are in this article; I'm not going to copy them here, but all of them are based on the same Base Runs equation and they all estimate RA, not ERA:

* eRA is based on the actual results allowed by the pitcher (hits, doubles, home runs, walks, strikeouts, etc.). It is park-adjusted by dividing by PF.

* dRA is the classic DIPS-style RA, assuming that the pitcher allows a league average %H, and that his hits in play have a league-average S/D/T split. It is park-adjusted by dividing by PF.

* cRA is based on batted ball type (FB, GB, POP, LD) allowed, using the actual estimated linear weight value for each batted ball type. It is not park-adjusted.

* sRA is a SIERA-style RA, based on batted balls but broken down into just groundballs and non-groundballs. It is not park-adjusted either.

Both cRA and sRA are running a little high when compared to actual RA for 2010. Both measures are very sensitive and need to be recalibrated in order to overcome batted ball-type definition differences, frequencies of hit types on each kind of batted ball, and other factors, so keep in mind that they may not perfectly track RA without those adjustments (which I have not made in this case). I’ll let you make your own determination as to whether you find this data useful at all. Personally, I prefer to look at RRA, eRA, and dRA.

G-F is a junk stat, included here out of habit because I've been including it for years. It was intended to give a quick read of a pitcher's expected performance in the next season, based on eRA and strikeout rate. Although the numbers vaguely resemble RAs, it's actually unitless. As a rule of thumb, anything under four is pretty good for a starter. G-F = 4.46 + .095(eRA) - .113(K*9/IP). It is a junk stat. JUNK STAT JUNK STAT JUNK STAT. Got it?

%H is BABIP, more or less; I use an estimate of PA (IP*x + H + W, where x is the league average of (AB - H)/IP). %H = (H - HR)/(IP*x + H - HR - K). Pitches/Start includes all appearances, so I've counted relief appearances as one-half of a start (P/S = Pitches/(.5*G + .5*GS). QS% is just QS/(G - GS); I don't think it's particularly useful, but Doug's Stats include QS so I include it.

I've used a stat called Relief Run Average (RRA) in the past, based on Sky Andrecheck's article in the August 1999 By the Numbers; that one only used inherited runners, but I've revised it to include bequeathed runners as well, making it equally applicable to starters and relievers. I am using RRA as the building block for baselined value estimates for all pitchers this year. I explained RRA in this article, but the bottom line formulas are:

BRSV = BRS - BR*i*sqrt(PF)
IRSV = IR*i*sqrt(PF) - IRS
RRA = ((R - (BRSV + IRSV))*9/IP)/PF

The two baselined stats are Runs Above Average (RAA) and Runs Above Replacement (RAR). RAA uses the league average runs/game (N) for both starters and relievers, while RAR uses separate replacement levels for starters and relievers. Thus, RAA and RAR will be pretty close for relievers:

RAA = (N - RRA)*IP/9
RAR (relievers) = (1.11*N - RRA)*IP/9
RAR (starters) = (1.28*N - RRA)*IP/9

All players with 285 or more plate appearances are included in the Hitters spreadsheets. (I usually use 300 as a cutoff, but this year when I had the list sorted there were a number of players just below 300 that I was interested in, so I chose an arbitrarily lower threshold). Each is assigned one position, the one at which they appeared in the most games. The statistics presented are: Games played (G), Plate Appearances (PA), Outs (O), Batting Average (BA), On Base Average (OBA), Slugging Average (SLG), Secondary Average (SEC), Runs Created (RC), Runs Created per Game (RG), Speed Score (SS), Hitting Runs Above Average (HRAA), Runs Above Average (RAA), Hitting Runs Above Replacement (HRAR), and Runs Above Replacement (RAR).

I do not bother to include hit batters, so take note of that for players who do get plunked a lot. Therefore, PA are simply AB + W. Outs are AB - H + CS. BA and SLG you know, but remember that without HB and SF, OBA is just (H + W)/(AB + W). Secondary Average = (TB - H + W)/AB = SLG - BA + (OBA - BA)/(1 - OBA). I have not included net steals as many people (and Bill James himself) do--it is solely hitting events.

BA, OBA, and SLG are park-adjusted by dividing by the square root of PF. This is an approximation, of course, but I'm satisfied that it works well. The goal here is to adjust for the win value of offensive events, not to quantify the exact park effect on the given rate. I use the BA/OBA/SLG-based formula to figure SEC, so it is park-adjusted as well.

Runs Created is actually Paul Johnson's ERP, more or less. Ideally, I would use a custom linear weights formula for the given league, but ERP is just so darn simple and close to the mark that it’s hard to pass up. I still use the term “RC” partially as a homage to Bill James (seriously, I really like and respect him even if I’ve said negative things about RC and Win Shares), and also because it is just a good term. I like the thought put in your head when you hear “creating” a run better than “producing”, “manufacturing”, “generating”, etc. to say nothing of names like “equivalent” or “extrapolated” runs. None of that is said to put down the creators of those methods--there just aren’t a lot of good, unique names available. Anyway, RC = (TB + .8H + W + .7SB - CS - .3AB)*.322.

RC is park adjusted by dividing by PF, making all of the value stats that follow park adjusted as well. RG, the rate, is RC/O*25.5. I do not believe that outs are the proper denominator for an individual rate stat, but I also do not believe that the distortions caused are that bad. (I still intend to finish my rate stat series and discuss all of the options in excruciating detail, but alas you’ll have to take my word for it now).

I have decided to switch to a watered-down version of Bill James' Speed Score this year; I only use four of his categories. Previously I used my own knockoff version called Speed Unit, but trying to keep it from breaking down every few years was a wasted effort.

Speed Score is the average of four components, which I'll call a, b, c, and d:

a = ((SB + 3)/(SB + CS + 7) - .4)*20
b = sqrt((SB + CS)/(S + W))*14.3
c = ((R - HR)/(H + W - HR) - .1)*25
d = T/(AB - HR - K)*450

James actually uses a sliding scale for the triples component, but it strikes me as needlessly complex and so I've streamlined it. I also changed some of his division to mathematically equivalent multiplications.

There are a whopping four categories that compare to a baseline; two for average, two for replacement. Hitting RAA compares to a league average hitter; it is in the vein of Pete Palmer’s Batting Runs. RAA compares to an average hitter at the player’s primary position. Hitting RAR compares to a “replacement level” hitter; RAR compares to a replacement level hitter at the player’s primary position. The formulas are:

HRAA = (RG - N)*O/25.5
RAA = (RG - N*PADJ)*O/25.5
HRAR = (RG - .73*N)*O/25.5
RAR = (RG - .73*N*PADJ)*O/25.5

PADJ is the position adjustment, and it is based on 1992-2001 offensive data. For catchers it is .89; for 1B/DH, 1.19; for 2B, .93; for 3B, 1.01; for SS, .86; for LF/RF, 1.12; and for CF, 1.02. It dawned on me when re-reading this before posting that the timeframe means that I’ve been using the same PADJ for ten years--which means two things:

1) I’m getting old
2) It’s probably time for an update. I’ll look at 2002-2011 in my forthcoming annual “Offense by Postion” post

That was the mechanics of the calculations; now I'll twist myself into knots trying to justify them. If you only care about the how and not the why, stop reading now.

The first thing that should be covered is the philosophical position behind the statistics posted here. They fall on the continuum of ability and value in what I have called "performance". Performance is a technical-sounding way of saying "Whatever arbitrary combination of ability and value I prefer".

With respect to park adjustments, I am not interested in how any particular player is affected, so there is no separate adjustment for lefties and righties for instance. The park factor is an attempt to determine how the park affects run scoring rates, and thus the win value of runs.

I apply the park factor directly to the player's statistics, but it could also be applied to the league context. The advantage to doing it my way is that it allows you to compare the component statistics (like Runs Created or OBA) on a park-adjusted basis. The drawback is that it creates a new theoretical universe, one in which all parks are equal, rather than leaving the player grounded in the actual context in which he played and evaluating how that context (and not the player's statistics) was altered by the park.

The good news is that the two approaches are essentially equivalent; in fact, they are equivalent if you assume that the Runs Per Win factor is equal to the RPG. Suppose that we have a player in an extreme park (PF = 1.15, approximately like Coors Field pre-humidor) who has an 8 RG before adjusting for park, while making 350 outs in a 4.5 N league. The first method of park adjustment, the one I use, converts his value into a neutral park, so his RG is now 8/1.15 = 6.957. We can now compare him directly to the league average:

RAA = (6.957 - 4.5)*350/25.5 = +33.72

The second method would be to adjust the league context. If N = 4.5, then the average player in this park will create 4.5*1.15 = 5.175 runs. Now, to figure RAA, we can use the unadjusted RG of 8:

RAA = (8 - 5.175)*350/25.5 = +38.77

These are not the same, as you can obviously see. The reason for this is that they take place in two different contexts. The first figure is in a 9 RPG (2*4.5) context; the second figure is in a 10.35 RPG (2*4.5*1.15) context. Runs have different values in different contexts; that is why we have RPW converters in the first place. If we convert to WAA (using RPW = RPG), then we have:

WAA = 33.72/9 = +3.75
WAA = 38.77/10.35 = +3.75

Once you convert to wins, the two approaches are equivalent. The other nice thing about the first approach is that once you park-adjust, everyone in the league is in the same context, and you can dispense with the need for converting to wins at all. You still might want to convert to wins, and you'll need to do so if you are comparing the 2010 players to players from other league-seasons (including between the AL and NL in the same year), but if you are only looking to compare Jose Bautista to Miguel Cabrera, it's not necessary. WAR is somewhat ubiquitous now, but personally I prefer runs when possible--why mess with decimal points if you don't have to?

The park factors used to adjust player stats here are run-based. Thus, they make no effort to project what a player "would have done" in a neutral park, or account for the difference effects parks have on specific events (walks, home runs, BA) or types of players. They simply account for the difference in run environment that is caused by the park (as best I can measure it). As such, they don't evaluate a player within the actual run context of his team's games; they attempt to restate the player's performance as an equivalent performance in a neutral park.

I suppose I should also justify the use of sqrt(PF) for adjusting component statistics. The classic defense given for this approach relies on basic Runs Created--runs are proportional to OBA*SLG, and OBA*SLG/PF = OBA/sqrt(PF)*SLG/sqrt(PF). While RC may be an antiquated tool, you will find that the square root adjustment is fairly compatible with linear weights or Base Runs as well. I am not going to take the space to demonstrate this claim here, but I will some time in the future.

Many value figures published around the sabersphere adjust for the difference in quality level between the AL and NL. I don't, but this is a thorny area where there is no right or wrong answer as far as I'm concerned. I also do not make an adjustment in the league averages for the fact that the overall NL averages include pitcher batting and the AL does not (not quite true in the era of interleague play, but you get my drift).

The difference between the leagues may not be precisely calculable, and it certainly is not constant, but it is real. If the average player in the AL is better than the average player in the NL, it is perfectly reasonable to expect the average AL player to have more RAR than the average NL player, and that will not happen without some type of adjustment. On the other hand, if you are only interested in evaluating a player relative to his own league, such an adjustment is not necessarily welcome.

The league argument only applies cleanly to metrics baselined to average. Since replacement level compares the given player to a theoretical player that can be acquired on the cheap, the same pool of potential replacement players should by definition be available to the teams of each league. One could argue that if the two leagues don't have equal talent at the major league level, they might not have equal access to replacement level talent--except such an argument is at odds with the notion that replacement level represents talent that is truly "freely available".

So it's hard to justify the approach I take, which is to set replacement level relative to the average runs scored in each league, with no adjustment for the difference in the leagues. The best justification is that it's simple and it treats each league as its own universe, even if in reality they are connected.

The replacement levels I have used here are very much in line with the values used by other sabermetricians. This is based both on my own "research", my interpretation of other's people research, and a desire to not stray from consensus and make the values unhelpful to the majority of people who may encounter them.

Replacement level is certainly not settled science. There is always going to be room to disagree on what the baseline should be. Even if you agree it should be "replacement level", any estimate of where it should be set is just that--an estimate. Average is clean and fairly straightforward, even if its utility is questionable; replacement level is inherently messy. So I offer the average baseline as well.

For position players, replacement level is set at 73% of the positional average RG (since there's a history of discussing replacement level in terms of winning percentages, this is roughly equivalent to .350). For starting pitchers, it is set at 128% of the league average RA (.380), and for relievers it is set at 111% (.450).

I am still using an analytical structure that makes the comparison to replacement level for a position player by applying it to his hitting statistics. This is the approach taken by Keith Woolner in VORP (and some other earlier replacement level implementations), but the newer metrics (among them Rally and Fangraphs' WAR) handle replacement level by subtracting a set number of runs from the player's total runs above average in a number of different areas (batting, fielding, baserunning, positional value, etc.), which for lack of a better term I will call the subtraction approach.

The offensive positional adjustment makes the inherent assumption that the average player at each position is equally valuable. I think that this is close to being true, but it is not quite true. The ideal approach would be to use a defensive positional adjustment, since the real difference between a first baseman and a shortstop is their defensive value. When you bat, all runs count the same, whether you create them as a first baseman or as a shortstop.

That being said, using “replacement hitter at position” does not cause too many distortions. It is not theoretically correct, but it is practically powerful. For one thing, most players, even those at key defensive positions, are chosen first and foremost for their offense. Empirical work by Keith Woolner has shown that the replacement level hitting performance is about the same for every position, relative to the positional average.

Figuring what the defensive positional adjustment should be, though, is easier said than done. Therefore, I use the offensive positional adjustment. So if you want to criticize that choice, or criticize the numbers that result, be my guest. But do not claim that I am holding this up as the correct analytical structure. I am holding it up as the most simple and straightforward structure that conforms to reality reasonably well, and because while the numbers may be flawed, they are at least based on an objective formula that I can figure myself. If you feel comfortable with some other assumptions, please feel free to ignore mine.

That still does not justify the use of HRAR--hitting runs above replacement--which compares each hitter, regardless of position, to 73% of the league average. Basically, this is just a way to give an overall measure of offensive production without regard for position with a low baseline. It doesn't have any real baseball meaning.

A player who creates runs at 90% of the league average could be above-average (if he's a shortstop or catcher, or a great fielder at a less important fielding position), or sub-replacement level (DHs that create 4 runs a game are not valuable properties). Every player is chosen because his total value, both hitting and fielding, is sufficient to justify his inclusion on the team. HRAR fails even if you try to justify it with a thought experiment about a world in which defense doesn't matter, because in that case the absolute replacement level (in terms of RG, without accounting for the league average) would be much higher than it is currently.

The specific positional adjustments I use are based on 1992-2001 data. There's no particular reason for not updating them; at the time I started using them, they represented the ten most recent years. I have stuck with them because I have not seen compelling evidence of a change in the degree of difficulty or scarcity between the positions between now and then, and because I think they are fairly reasonable. The positions for which they diverge the most from the defensive position adjustments in common use are 2B, 3B, and CF. Second base is considered a premium position by the offensive PADJ (.94), while third base and center field are both neutral (1.01 and 1.02).

Another flaw is that the PADJ is applied to the overall league average RG, which is artificially low for the NL because of pitcher's batting. When using the actual league average runs/game, it's tough to just remove pitchers--any adjustment would be an estimate. If you use the league total of runs created instead, it is a much easier fix.

One other note on this topic is that since the offensive PADJ is a proxy for average defensive value by position, ideally it would be applied by tying it to defensive playing time. I have done it by outs, though.

The reason I have taken this flawed path is because 1) it ties the position adjustment directly into the RAR formula rather then leaving it as something to subtract on the outside and more importantly 2) there’s no straightforward way to do it. The best would be to use defensive innings--set the full-time player to X defensive innings, figure how Derek Jeter’s innings compared to X, and adjust his PADJ accordingly. Games in the field or games played are dicey because they can cause distortion for defensive replacements. Plate Appearances avoid the problem that outs have of being highly related to player quality, but they still carry the illogic of basing it on offensive playing time. And of course the differences here are going to be fairly small (a few runs). That is not to say that this way is preferable, but it’s not horrible either, at least as far as I can tell.

To compare this approach to the subtraction approach, start by assuming that a replacement level shortstop would create .86*.73*4.5 = 2.825 RG (or would perform at an overall level of equivalent value to being an average fielder at shortstop while creating 2.825 runs per game). Suppose that we are comparing two shortstops, each of whom compiled 600 PA and played an equal number of defensive games and innings (and thus would have the same positional adjustment using the subtraction approach). Alpha made 380 outs and Bravo made 410 outs, and each ranked as dead-on average in the field.

The difference in overall RAR between the two using the subtraction approach would be equal to the difference between their offensive RAA compared to the league average. Assuming the league average is 4.5 runs, and that both Alpha and Bravo created 75 runs, their offensive RAAs are:

Alpha = (75*25.5/380 - 4.5)*380/25.5 = +7.94

Similarly, Bravo is at +2.65, and so the difference between them will be 5.29 RAR.

Using the flawed approach, Alpha's RAR will be:

(75*25.5/380 - 4.5*.73*.86)*380/25.5 = +32.90

Bravo's RAR will be +29.58, a difference of 3.32 RAR, which is two runs off of the difference using the subtraction approach.

The downside to using PA is that you really need to consider park effects if you, whereas outs allow you to sidestep park effects. Outs are constant; plate appearances are linked to OBA. Thus, they not only depend on the offensive context (including park factor), but also on the quality of one's team. Of course, attempting to adjust for team PA differences opens a huge can of worms which is not really relevant; for now, the point is that using outs for individual players causes distortions, sometimes trivial and sometimes bothersome, but almost always makes one's life easier.

I do not include fielding (or baserunning outside of steals, although that is a trivial consideration in comparison) in the RAR figures--they cover offense and positional value only). This in no way means that I do not believe that fielding is an important consideration in player valuation. However, two of the key principles of these stat reports are 1) not incorporating any data that is not readily available and 2) not simply including other people's results (of course I borrow heavily from other people's methods, but only adapting methodology that I can apply myself).

Any fielding metric worth its salt will fail to meet either criterion--they use zone data or play-by-play data which I do not have easy access to. I do not have a fielding metric that I have stapled together myself, and so I would have to simply lift other analysts' figures.

Setting the practical reason for not including fielding aside, I do have some reservations about lumping fielding and hitting value together in one number because of the obvious differences in reliability between offensive and fielding metrics. In theory, they absolutely should be put together. But in practice, I believe it would be better to regress the fielding metric to a point at which it would be roughly equivalent in reliability to the offensive metric.

Offensive metrics have error bars associated with them, too, of course, and in evaluating a single season's value, I don't care about the vagaries that we often lump together as "luck". Still, there are errors in our assessment of linear weight values and players that collect an unusual proportion of infield hits or hits to the left side, errors in estimation of park factor, and any number of other factors that make their events more or less valuable than an average event of that type.

Fielding metrics offer up all of that and more, as we cannot be nearly as certain of true successes and failures as we are when analyzing offense. Recent investigations, particularly by Colin Wyers, have raised even more questions about the level of uncertainty. So, even if I was including a fielding value, my approach would be to assume that the offensive value was 100% reliable (which it isn't), and regress the fielding metric relative to that (so if the offensive metric was actually 70% reliable, and the fielding metric 40% reliable, I'd treat the fielding metric as .4/.7 = 57% reliable when tacking it on, to illustrate with a simplified and completely made up example presuming that one could have a precise estimate of nebulous "reliability").

Given the inherent assumption of the offensive PADJ that all positions are equally valuable, once RAR has been figured for a player, fielding value can be accounted for by adding on his runs above average relative to a player at his own position. If there is a shortstop that is -2 runs defensively versus an average shortstop, he is without a doubt a plus defensive player, and a more valuable defensive player than a first baseman who was +1 run better than an average first baseman. Regardless, since it was implicitly assumed that they are both average defensively for their position when RAR was calculated, the shortstop will see his value docked two runs. This DOES NOT MEAN that the shortstop has been penalized for his defense. The whole process of accounting for positional differences, going from hitting RAR to positional RAR, has benefited him.

I've found that there is often confusion about the treatment of first baseman and designated hitters in my PADJ methodology, since I consider DHs as in the same pool as first baseman. The fact of the matter is that first baseman outhit DH. There is any number of potential explanations for this; DHs are often old or injured, players hit worse when DHing than they do when playing the field, etc. This actually helps first baseman, since the DHs drag the average production of the pool down, thus resulting in a lower replacement level than I would get if I considered first baseman alone.

However, this method does assume that a 1B and a DH have equal defensive value. Obviously, a DH has no defensive value. What I advocate to correct this is to treat a DH as a bad defensive first baseman, and thus knock another five or ten runs off of his RAR for a full-time player. I do not incorporate this into the published numbers, but you should keep it in mind. However, there is no need to adjust the figures for first baseman upwards --the only necessary adjustment is to take the DHs down a notch.

Finally, I consider each player at his primary defensive position (defined as where he appears in the most games), and do not weight the PADJ by playing time. This does shortchange a player like Ben Zobrist (who saw significant time at a tougher position than his primary position), and unduly boost a player like Buster Posey (who logged a lot of games at a much easier position than his primary position). For most players, though, it doesn't matter much. I find it preferable to make manual adjustments for the unusual cases rather than add another layer of complexity to the whole endeavor.

Player spreadsheets should be coming by the middle of the week.

2011 Park Factors

2011 Leagues

2011 Teams

2011 Team Offense

2011 Team Defense

2011 AL Relievers

2011 NL Relievers

2011 AL Starters

2011 NL Starters

2011 AL Hitters

2011 NL Hitters