Hitting by Lineup Position, 2016

I devoted a whole post to leadoff hitters, whether justified or not, so it's only fair to have a post about hitting by batting order position in general. I certainly consider this piece to be more trivia than sabermetrics, since there’s no analytic content.

The data in this post was taken from Baseball-Reference. The figures are park-adjusted. RC is ERP, including SB and CS, as used in my end of season stat posts. The weights used are constant across lineup positions; there was no attempt to apply specific weights to each position, although they are out there and would certainly make this a little bit more interesting:



The seven year run of NL #3 hitters as the best position in baseball was snapped, albeit by an insignificant .01 RG by AL #3 hitters. Since Mike Trout’s previous career high in PA out of the #3 spot was 336 in 2015 and he racked up 533 this year, I’m going to give full credit to Trout; as we will see in a moment, the Angels’ #3 hitters were the best single lineup spot in baseball. #2 hitters did not outperform #5 in both circuits as they did last year, just the AL. However, the NL made up for hit by having their leadoff hitters create runs at almost the exact same rate as their #5s.

Next are the team leaders and trailers in RG at each lineup position. The player listed is the one who appeared in the most games in that spot (which can be misleading, especially for spots low in the batting order where many players cycle through):





A couple things that stood out to me was St. Louis’ dominance at the bottom of the order and the way in which catchers named Perez managed to sabotage lineup spots for two teams. Apologies to Carlos Beltran (the real culprits for the poor showing of Texas #3 hitters were Adrian Beltre, Prince Fielder, and Nomar Mazara) and Luis Valbuena (Carlos Gomez and Marwin Gonzalez).

The case of San Diego’s cleanup hitters deserves special attention. Yangervis Solarte was actually pretty good when batting cleanup, as his .289/.346/.485 line in 289 PA compares favorably to the NL average for cleanup hitters. The rest of the Padres who appeared in that spot combined for 399 PA with a dreadful .187/.282/.336 line. Just to give you a quick idea of how bad this is, the 618 OPS would have been the eleventh-worst among any non-NL #9 lineup spot in the majors, leading only 6 AL #9s, 2 #2s, a #7, and the horrible Oakland #2s. It was also worse than the Cardinals’ #9 hitters.

The next list is the ten best positions in terms of runs above average relative to average for their particular league spot (so AL leadoff spots are compared to the AL average leadoff performance, etc.):



And the ten worst:



Joe Mauer himself wasn’t that bad, with a 799 OPS when hitting third. That’s still well-below the AL average, but not bottom ten in RAA bad without help from his friends.

The last set of charts show each team’s RG rank within their league at each lineup spot. The top three are bolded and the bottom three displayed in red to provide quick visual identification of excellent and poor production:





The full spreadsheet is available here.

Leadoff Hitters, 2016

I will try to make this as clear as possible: the statistics are based on the players that hit in the #1 slot in the batting order, whether they were actually leading off an inning or not. It includes the performance of all players who batted in that spot, including substitutes like pinch-hitters.

Listed in parentheses after a team are all players that started in twenty or more games in the leadoff slot--while you may see a listing like "COL (Blackmon)" this does not mean that the statistic is only based solely on Blackmon's performance; it is the total of all Colorado batters in the #1 spot, of which Blackmon was the only one to start in that spot in twenty or more games. I will list the top and bottom three teams in each category (plus the top/bottom team from each league if they don't make the ML top/bottom three); complete data is available in a spreadsheet linked at the end of the article. There are also no park factors applied anywhere in this article.

That's as clear as I can make it, and I hope it will suffice. I always feel obligated to point out that as a sabermetrician, I think that the importance of the batting order is often overstated, and that the best leadoff hitters would generally be the best cleanup hitters, the best #9 hitters, etc. However, since the leadoff spot gets a lot of attention, and teams pay particular attention to the spot, it is instructive to look at how each team fared there.

The conventional wisdom is that the primary job of the leadoff hitter is to get on base, and most simply, score runs. It should go without saying on this blog that runs scored are heavily dependent on the performance of one’s teammates, but when writing on the internet it’s usually best to assume nothing. So let's start by looking at runs scored per 25.5 outs (AB - H + CS):

1. HOU (Springer/Altuve), 6.9
2. COL (Blackmon), 6.7
3. DET (Kinsler), 6.6
Leadoff average, 5.2
ML average, 4.5
28. SF (Span), 4.4
29. KC (Escobar/Dyson/Merrifield), 4.1
30. OAK (Crisp/Burns), 3.4

Again, no park adjustments were applied, so the Rockies performance was good but it wasn’t really “best in the NL good”. I’m also going to have a hard time resisting just writing “Esky Magic” every time the Royals appear on a trailers list.

The most basic team independent category that we could look at is OBA (figured as (H + W + HB)/(AB + W + HB)):

1. CHN (Fowler/Zobrist), .383
2. HOU (Springer/Altuve), .375
3. STL (Carpenter), .370
Leadoff average, .341
ML average, .324
28. WAS (Turner/Revere/Taylor), .305
29. KC (Escobar/Dyson/Merrifield), .298
30. OAK (Crisp/Burns), .290

Esky Magic. And once again Billy Burns chipping in to Oakland’s anemic showing and of course Kansas City just had to have Billy Burns.

The next statistic is what I call Runners On Base Average. The genesis for ROBA is the A factor of Base Runs. It measures the number of times a batter reaches base per PA--excluding homers, since a batter that hits a home run never actually runs the bases. It also subtracts caught stealing here because the BsR version I often use does as well, but BsR versions based on initial baserunners rather than final baserunners do not. Here ROBA = (H + W + HB - HR - CS)/(AB + W + HB).

This metric has caused some confusion, so I’ll expound. ROBA, like several other methods that follow, is not really a quality metric, it is a descriptive metric. A high ROBA is a good thing, but it's not necessarily better than a slightly lower ROBA plus a higher home run rate (which would produce a higher OBA and more runs). Listing ROBA is not in any way, shape or form a statement that hitting home runs is bad for a leadoff hitter. It is simply a recognition of the fact that a batter that hits a home run is not a baserunner. Base Runs is an excellent model of offense and ROBA is one of its components, and thus it holds some interest in describing how a team scored its runs, rather than how many it scored:

1. CHN (Fowler/Zobrist), .351
2. MIA (Gordon/Suzuki/Dietrich/Realmuto), .335
3. ATL (Inciarte/Peterson/Markakis), .331
4. HOU (Springer/Altuve), .331
Leadoff average, .305
ML average, .287
28. TEX (Choo/Odor/DeShields/Profar), .264
29. WAS (Turner/Revere/Taylor), .260
30. MIN (Dozier/Nunez), .256

Kansas City leadoff hitters finished tied for last in the majors with five home runs (with Miami), so Esky Magic was only good for 23rd place. Twins leadoff hitters, thanks primarily to Dozier, led the majors with 39 homers. So only after around 25.6% of leadoff hitter plate appearances did they actually wind up with a runner on base. Their .320 OBA was well-below average too, but again ROBA describes how an offense plays out--other considerations are necessary to determine how good it was.

I also include what I've called Literal OBA--this is just ROBA with HR subtracted from the denominator so that a homer does not lower LOBA, it simply has no effect. It “literally” (not really, thanks to errors, out stretching, caught stealing after subsequent plate appearances, etc.) is the proportion of plate appearances in which the batter becomes a baserunner able to be advanced by his teammates. You don't really need ROBA and LOBA (or either, for that matter), but this might save some poor message board out there twenty posts, by not implying that I think home runs are bad, so here goes. LOBA = (H + W + HB - HR - CS)/(AB + W + HB - HR):

1. CHN (Fowler/Zobrist), .360
2. HOU (Springer/Altuve), .344
3. STL (Carpenter), .342
Leadoff average, .313
ML average, .297
28. OAK (Crisp/Burns), .273
29. MIN (Dozier/Nunez), .270
30. WAS (Turner/Revere/Taylor), .268

The next two categories are most definitely categories of shape, not value. The first is the ratio of runs scored to RBI. Leadoff hitters as a group score many more runs than they drive in, partly due to their skills and partly due to lineup dynamics. Those with low ratios don’t fit the traditional leadoff profile as closely as those with high ratios (at least in the way their seasons played out):

1. MIA (Gordon/Suzuki/Dietrich/Realmuto), 2.6
2. SD (Jankowski/Jay), 2.3
3. ATL (Inciarte/Peterson/Markakis), 2.0
6. LAA (Escobar/Calhoun), 1.9
Leadoff average, 1.5
ML average, 1.0
26. STL (Carpenter), 1.3
28. BOS (Betts/Pedroia), 1.2
29. OAK (Crisp/Burns), 1.2
30. MIN (Dozier/Nunez), 1.1

This speaks more to me than the measure, but the most interesting thing I learned from that list was that Travis Jankowski was San Diego’s primary leadoff hitter (71 games). Looking at the rest of the list, I think I could have guessed most team’s in two or three, I never would have gotten the Padres.

A similar gauge, but one that doesn't rely on the teammate-dependent R and RBI totals, is Bill James' Run Element Ratio. RER was described by James as the ratio between those things that were especially helpful at the beginning of an inning (walks and stolen bases) to those that were especially helpful at the end of an inning (extra bases). It is a ratio of "setup" events to "cleanup" events. Singles aren't included because they often function in both roles.

Of course, there are RBI walks and doubles are a great way to start an inning, but RER classifies events based on when they have the highest relative value, at least from a simple analysis:

1. MIA (Gordon/Suzuki/Dietrich/Realmuto), 1.8
2. ATL (Inciarte/Peterson/Markakis), 1.4
3. PHI (Herrera/Hernandez), 1.4
6. NYA (Ellsbury/Gardner), 1.2
Leadoff average, .8
ML average, .7
26. COL (Blackmon), .5
28. TB (Forsythe/Guyer), .5
29. DET (Kinsler), .5
30. BAL (Jones/Rickard), .4

The Orioles certainly had a non-traditional leadoff profile thanks mostly to Jones; their five stolen base attempts was the fewest of any team, they were tied for third with 30 homers, and they drew 20 less walks than an average team out of the leadoff spot.

Since stealing bases is part of the traditional skill set for a leadoff hitter, I've included the ranking for what some analysts call net steals, SB - 2*CS. I'm not going to worry about the precise breakeven rate, which is probably closer to 75% than 67%, but is also variable based on situation. The ML and leadoff averages in this case are per team lineup slot:

1. WAS (Turner/Revere/Taylor), 30
2. MIL (Villar/Santana), 27
3. MIA (Gordon/Suzuki/Dietrich/Realmuto), 22
4. CLE (Santana/Davis), 20
Leadoff average, 6
ML average, 2
28. TB (Forsythe/Guyer), -11
29. SEA (Aoki/Martin), -13
30. PHI (Herrera/Hernandez), -16

The Indians are a good example of why I list all players who had at least twenty starts in the leadoff spot; AL steal leader Rajai Davis’ 69 games leading off led to them leading the AL in net steals.

Shifting back to quality measures, first up is one that David Smyth proposed when I first wrote this annual leadoff review. Since the optimal weight for OBA in a x*OBA + SLG metric is generally something like 1.7, David suggested figuring 2*OBA + SLG for leadoff hitters, as a way to give a little extra boost to OBA while not distorting things too much, or even suffering an accuracy decline from standard OPS. Since this is a unitless measure anyway, I multiply it by .7 to approximate the standard OPS scale and call it 2OPS:

1. COL (Blackmon), 880
2. BOS (Betts/Pedroia), 872
3. HOU (Springer/Altuve), 865
Leadoff average, 775
ML average, 745
28. SF (Span), 722
29. OAK (Crisp/Burns), 654
30. KC (Escobar/Dyson/Merrifield), 650

Esky Magic.

Along the same lines, one can also evaluate leadoff hitters in the same way I'd go about evaluating any hitter, and just use Runs Created per Game with standard weights (this will include SB and CS, which are ignored by 2OPS):

1. COL (Blackmon), 6.4
2. BOS (Betts/Pedroia), 6.3
3. HOU (Springer/Altuve), 6.2
Leadoff average, 4.9
ML average, 4.5
28. SF (Span), 4.1
29. KC (Escobar/Dyson/Merrifield), 3.4
30. OAK (Crisp/Burns), 3.3

Esky Magic.

The same six teams make up the leaders and trailers, which shouldn’t be a big surprise.

Allow me to close with a crude theoretical measure of linear weights supposing that the player always led off an inning (that is, batted in the bases empty, no outs state). There are weights out there (see The Book) for the leadoff slot in its average situation, but this variation is much easier to calculate (although also based on a silly and impossible premise).

The weights I used were based on the 2010 run expectancy table from Baseball Prospectus. Ideally I would have used multiple seasons but this is a seat-of-the-pants metric. The 2010 post goes into the detail of how this measure is figured; this year, I’ll just tell you that the out coefficient was -.224, the CS coefficient was -.591, and for other details refer you to that post. I then restate it per the number of PA for an average leadoff spot (746 in 2014):

1. HOU (Springer/Altuve), 30
2. COL (Blackmon), 28
3. CHN (Fowler/Zobrist), 27
Leadoff average, 7
ML average, 0
28. SF (Span), -8
29. KC (Escobar/Dyson/Merrifield), -19
30. OAK (Crisp/Burns), -21

Esky Magic. Lest anyone think I am being unduly critical of Escobar's performance (he did after all start only half (actually 82) of KC's games as the leadoff hitter), note that Escobar when in the #1 spot hit .242/.272/.289. The rest of the Royals combined for .274/.317/.378, which would only rank second worst in the majors in 2OPS. So the Royals team performance was terrible, but Escobar was dreadful. Just the worst.

The spreadsheet with full data is available here.

Statistical Meanderings, 2016

What follows is an abbreviated version of my annual collection of oddities that jump out at me from the year-end statistical reports I publish on this blog. These tidbits are intended as curiosities rather than as sober sabermetric analysis:

* The top ten teams in MLB in W% were the playoff participants. The top six were the division winners. A rare case in which obvious inequities aren't created by micro-divisions, in stark constant to 2015's NL Central debacle.

* In the NL, only Washington (.586) had a better overall W% than Chicago's road W% (.575). Of course, the Cubs were a truly great team, and with 103 wins and a world title on the heels of 97 wins a year ago, they belong in any discussion of the greatest teams of all-time. In Baseball Dynasties, Eddie Epstein and Rob Neyer used three years as their base time period for ranking the greatest dynasties. Another comparable regular season in 2017, regardless of playoff result, would in my opinion place the Cubs forwardly on a similarly-premised list.

Most impressive about the Cubs is that despite winning 103, their EW% (.667) and PW% (.660) outpaced their actual W% of .640.

* It is an annual tradition to run a chart in this space that compares the offensive and defensive runs above average for each of the playoff teams. RAA is figured very simply here by comparing park adjusted runs or runs allowed per game to the league average. Often I enjoy showing that the playoff teams were stronger offensively than defensively, but that was not the case in 2016:



This is another way to show just how great the Cubs were--only two other playoff teams were as many as 80 RAA on either side of the scorecard and the Cubs were +101 offensively and +153 defensively.

* The Twins have a multi-year run of horrible starting pitching, and 2016 only added to the misery. Only the Angels managed a worse eRA from their starters (5.61 to 5.58); only A's starters logged fewer innings per start among AL teams (5.39 to 5.40); and the Twins were dead last in the majors in QS% (36%). In their surprising contention blip of 2015, the Twins were only in the bottom third of the AL in starting pitching performance, but in 2014 they were last in the majors in eRA, second-last in IP/S (ahead of only Colorado and QS%; in 2013 they were last in all three categories; and in 2012 they were last in the majors in eRA and second-last in IP/S and QS%.

* There were a lot of great things from my perspective about the 2016 season from a team performance perspective, chiefly the Indians winning the pennant and playoffs in which the lesser participants did not advance their way through. Both were helped along by the comeuppance finally delivered to the Royals. It wasn't quite as glorious as it might have been, as they still managed to scrap out a .500 record, but the fundamental problems with their vaunted contact offense were laid bare. KC was easily the lowest scoring team in the AL at 4.05 R/G, with the Yankees of all teams second-worst with 4.19. They were last in the majors with .075 walks/at bat (COL, .084 was second worst). They were last in the AL in isolated power by 12 points (.137) and beat out only Atlanta and Miami, edging out the 30th-ranked Braves by just .007 points. Combining those two, their .212 secondary average was sixteen points lower than the Marlins for last in the majors. But they were at the AL average in batting average at .257, so that's something.

* Andrew Miller averaged 17.1 strikeouts and 1.3 walks per 37.2 plate appearances (I use the league average of PA/G for to rest K and W rate per PA on the familiar scale of per nine innings while still using the proper denominator of PA). If you halve his K rate and double his walk rate, that's 8.6 and 2.6, which is still a pretty solid reliever. A comparable but slightly inferior performer this year was Tony Watson (8.2 and 2.8).

* Boston's bullpen was built (or at least considered by some preseason) to be a lockdown unit with Tazawa, Uehara, and Kimbrel. Tazawa had a poor season with 0 RAR; Uehara and Kimbrel missed some time with injuries and were just okay when they pitched for 10 RAR each. Combined they had 20 RAR. Dan Otero, a non-roster invitee to spring training with Cleveland, had 26 RAR.

* Matt Albers (-18) had the lowest RAR of anyone who qualified for any of my individual stat reports. I don't think that save is very likely at this point.

* Just using your impression of Toronto's starters, their talent/stuff/age/etc., just try to associate each to their strikeout and walk rates (the five pitchers are RA Dickey, Marco Estrada, JA Happ, Aaron Sanchez, and Marcus Stroman):



The correct answer from A to E is Dickey, Sanchez, Stroman, Estrada, Happ. I never got a chance to play this game without being spoiled, but I'm certain that I would have at least said that Aaron Sanchez was pitcher D.

* Jameson Taillon made it to the majors at age 25, and the thing that jumped out at me from his stat line was his very low walk rate (1.5, lower than any NL starter with 15 starts save Clayton Kershaw and Bartolo Colon. note that Taillon just cleared the bar for inclusion).

John Lackey, at age 38, chipped in 49 RAR to Chicago (granted, fielding support contributed to his performance). Taillon and Lackey are always linked in my head thanks to a Fangraphs prospect post from several years ago that I will endeavor to find. I believe the Fangraphs writer offered Lackey as a comp for Taillon. A commenter, perhaps a Pittsburgh partisan, responded by saying it was a ridiculous comparison, essentially an insult to Taillon.

My thought at the time was that if I had any pitching prospect in the minors, and you told me that if I signed on the dotted line he would wind up having John Lackey's career, I would take it every time. That's not to say that there aren't pitchers in the minors who won't exceed Lackey's career, but to think that it's less than the median likely outcome for any pitching prospect is pretty aggressive. And this was before Lackey's late career performance which has further bolstered his standing. What odds would you place now on Jameson Taillon having a better career than John Lackey?

* Jeff Francoeur had exactly 0 RAR. Ryan Howard had 1, before fielding/baserunning which would push him negative.

* I mentioned in my MVP post how unique it was that Kyle and Corey Seager were both worthy of being on the MVP ballot. They performed fairly comparably across the board:



Chase and Travis d'Arnaud also had pretty similar numbers. Not good numbers, but similar nonetheless (which in Chase's case was probably a triumph whilst a disappointment for Travis):



* It wouldn't be a meanderings post without some Indians-specific comments. It has actually been harder than usual to move on to writing the year-end posts because of the disappointment of seeing the Indians lose their second, third, and fourth-consecutive games with a chance to close out the World Series. Three of those losses have come by one run and two in Game 7 in extra innings. The Indians have now gone 68 seasons without winning the World Series, losing four consecutive World Series after winning the first two in franchise history. That now matches the record of the Red Sox from 1918 - 1986, which if Ken Burns' "Baseball" and plagiarist/self-proclaimed patron saint of sad sack franchises Doris Kearns Goodwin are to believed was a level of baseball fan suffering unmatched and possibly comparable to the Battle of Stalingrad. Well, except for the initial two World Series winning streak--Boston won their first four World Series.

The two Cleveland notes I have are negative, which is only because I have been thinking about them in conjunction with Game 7. One is how bad Yan Gomes was this season, creating just 1.9 runs per game over 262 PA, dead last in the AL among players with 250 or more PA. I did not understand Terry Francona's decision to pinch-run for Roberto Perez with the Indians down multiple runs in the seventh inning. He must have felt that a basestealing threat would distract Jon Lester, but given the inning and the extent of Cleveland's deficit, it basically ensured that Gomes would have to bat at some point. And bat he did, with the go-ahead run on first and two outs in the eighth against a laboring Chapman who had just coughed up the lead.

Also costly was the decision to bring Michael Martinez in to play outfield in the ninth. That move made more sense given Coco Crisp's noodle arm, but to see Martinez make the last out was a tough pill to swallow (and had Martinez somehow reached base, Gomes would have followed). And don't even get me started on the intentional walks in the tenth inning.

Also, it must be noted that Mike Napoli, who struggled in the postseason, was a very average performer in the regular season, creating 5.2 runs per game as first baseman. This is not intended as a criticism of Napoli, especially since I have been kvetching for years about the Indians inability to get even average production out of the corners. Napoli fit that need perfectly. But it felt as if the fans and media evaluated his performance as better than that (even limited strictly to production in the batter's box and not alleged leadership/veteran presence/etc.)

* For various reasons, a few of the players who were in the thick of the NL MVP race a year ago and were surely considered favorites coming into this season had disappointing seasons. These three outfielders (Bryce Harper, Andrew McCutchen, Giancarlo Stanton) all wound up fairly close in 2016 RAR (28, 27, 23 respectively), yielding the MVP center stage to youngsters (Kris Bryant and Corey Seager), first basemen (Freddie Freeman, Anthony Rizzo, Joey Votto) and a guy having a career year (Daniel Murphy).

More interestingly, those big three outfielders combined for 78 RAR--five fewer than Mike Trout.

Hypothetical Ballot: Cy Young

There are no particular standout candidates for the Cy Young in either league, and I was tempted to open up this post by saying something like “Maybe it is a harbinger of things to come, as starting pitchers workloads continue to decrease and more managers consider times through the order in making the decision to go to the bullpen…we can expect more seasons like this, where no Cy Young contender really distinguishes himself.”

And then I stopped and concluded, “You idiot, don’t you dare write that.” This is exactly the kind of banal over-extrapolation of heavily selected data that I rail against constantly. In the long run, is it possible that those factors could contribute to a dilution of clear Cy Young candidates, leaving voters to comb over a pack of indistinguishable guys pitching 180 innings a year? Entirely possible. Does that make 2016 the new normal? Of course not. Just last year, there was an epic three-way NL Cy Young race. This year, only an injury to Clayton Kershaw seems to have stood in the way of a historic season and Cy Young landslide.

In the AL race, Justin Verlander had a 70 to 61 RAR lead over Chris Sale, with a pack of pitchers right behind them (Rick Porcello 59, Corey Kluber 58, Jose Quintana 57, Aaron Sanchez/JA Happ/Masahiro Tanaka 56). Convieniently, the first four in RAR also are the only pitchers who would also have 50 or more RAR based on eRA or dRA, with one exception. Verlander allowed a BABIP of just .261 and would so his dRA is 3.80, significantly higher than his 3.04 RRA. However, none of the others look better using dRA--all three are five to eight runs worse. So I go with Verlander for the top spot and Porcello second over Sale (he led the AL with a 3.14 eRA, and since we are talking about one run differences here, Bill James would at least want us to consider his 22-4 W-L record). I didn’t actually consider the W-L record, but he does rank just ahead of Sale if you weight RAR from actual/eRA/dRA at 50%/30%/20%, which has no scientific basis but seems reasonable enough. Again, there’s only a one RAR difference between Sale and Porcello, so using W-L or flipping a coin to order them is just as reasonable. I gave the fifth spot to Jose Quintana over Aaron Sanchez, and would not have guessed that Quintana had a better strikeout rate (8.1 to 7.8).

This leaves out Zach Britton, who I credit with just 35 RAR. I remain thoroughly unconvinced that leverage bonuses are appropriate. Each run allowed and out recorded is worth the same to the final outcome regardless of what inning it comes in. The difference between starters and relief aces is that some of the games the former pitch could have been won or lost with worse or better performances, while relief aces generally are limited to pitching in close games. But the fact that Britton pitches the ninth doesn’t make his shutout inning any more valuable than the one Chris Tillman pitched in the fourth within the context of that single game. To the extent that Britton contributes more value on a per inning basis, it’s because he pitched in a greater proportion of games in which one run might have made a difference, not because that is more apparent for any particular game at the point at which Britton appears in it than it was when the starter was pitching. I have alluded to this viewpoint many times, but have never written it up satisfactorily because I’ve not figured out how to propose a leverage adjustment that captures it, without going to the extreme that value can only be generated by pitching in games your team wins.

1. Justin Verlander, DET
2. Rick Porcello, BOS
3. Chris Sale, CHA
4. Corey Kluber, CLE
5. Jose Quintana, CHA

In the NL, there were seven starters with 60 RAR and then a gap of four to Jake Arrieta, which makes a good cohort to consider for the ballot. Of this group, Tanner Roark and Madison Bumgarner at the bottom in terms of RAR and had high dRAs (4.17 and 3.87) which justify dropping them.

That leaves Jon Lester (71 RAR), Kyle Hendricks (70), Max Scherzer (70), Johnny Cueto (65), and Clayton Kershaw (64). If you weight 50/30/20 as for the AL, all five are clustered between 60 and 64 RAR. This makes it tempting to just to pick Kershaw as he was much the best in every rate and narrowly missed leading the league in RAA despite pitching only 149 innings.

Among the four who pitched full seasons, Scherzer ranks first in innings and third in RRA, eRA, and dRA. However, he pitched significantly more innings than the Cubs candidates--25 more than Lester and 38 more than Hendricks. Comparing him to Cueto, who pitched nine fewer innings, Scherzer leads in RRA by .09 runs, eRA by .13 runs, and trails in dRA by .09 runs. So for my money Scherzer provided the best mix of effectiveness and durability.

All that’s left is a direct comparison of Scherzer to Kershaw, in which I think the innings gap is just too great without giving excessive weight to peripherals. The difference between Scherzer and Kershaw is 79 innings with a 3.62 RRA. To put it in 2016 performance terms, that makes Scherzer equivalent to Kershaw plus a solid reliever like Felipe Rivero or Travis Wood. That’s too much value for me to ignore looking at the gaudy (and they are gaudy!) rate stats:

1. Max Scherzer, WAS
2. Jon Lester, CHN
3. Kyle Hendricks, CHN
4. Clayton Kershaw, LA
5. Johnny Cueto, SF

Hypothetical Ballot: MVP

You could basically copy and paste the same thing for AL MVP every year, so I’ll try to keep it brief. My position is that wins are value, and 8 wins don’t count for more because the rest of your teammates were worth 50 than if the rest of your teammates were only worth 30.

But the debate over the definition of value is not what I find most obnoxious about the Mike Trout-era MVP discussions. It’s easy enough to disagree on that point and move one. What is most bothersome is the way that people attempt to co-opt the sabermetric terms that sound sabermetric like “error bars” to push their own narratives.

Let’s suppose that Player A is estimated to have contributed 87 RAR and player B is estimated to have contributed 80 RAR, and that the standard error is something like 10 runs. In this case, it certainly is inconclusive that player A was truly more valuable than player B. I would grant that player B would be a reasonable choice as MVP.

But if you’re filing out your MVP ballot, *should* you put Player B ahead of Player A? It’s still quite likely that Player A was more valuable than Player B. To me, you need to have a good reason to put Player B ahead, particularly when the margin is “significant” but not beyond the “error bar”.

Worse yet, though, is the attempt to twist oneself into a pretzel to make up those good reasons. The real gem going around, which you will see in comment sections and message boards, is that the error bars must be larger for Player A. Because you see, Player A’s park became a strong pitcher’s park right around when he arrived, and parks don’t change character like that (says someone who has never examined historical park factors). Because you see, Player A always leads the league in RAR, and by a wide margin--that just can’t be right. Player A is so consistently great in the metrics that the metrics must be wrong.

The world is not worthy of Player A. Every week of Player A’s career is scrutinized by pseudo-sabermetricians who have deadlines to fill with their micro-analytical pablum, and who when they aren’t vulturing over Player A are busy writing extrapolating trends from blips in thirty-team samples to blame metrics for their own arrogance. Player A can’t win with the people who should be appreciating him--not in the sense that a fan might but exactly in the sense that a detached analyst would.

I’m sure you’ve deduced by now that Player A is Mike Trout, and you may have guessed that Player B is Mookie Betts. Except those aren’t even my true estimates of their RAR, they’re what I would come up with their RAR if I took my hitting/position RAR + BP’s baserunning runs (for non-steals, since steals are incorporated in the first piece) + the average of each player’s BP FRAA, BIS DRS, and MGL UZR. In other words, if I didn’t regress fielding at all, which I don’t think is the correct position. When adding components together, if one (hitting) is more reliable than another (fielding), it doesn’t make sense to ignore that. In actually estimating RAR for the purpose of filling out a fake MVP ballot, I used 50% FRAA, 25% DRS, 25% UZR, and halved it. Then Trout is at 86 RAR, Betts 68, and Jose Alutve slides in between them at 71, which explains the top of my ballot.

If anything, I think I may be generous to Betts, who needs all of his 8 baserunning runs and 11 “regressed” fielding runs to overcome 49 hitting RAR, which ranked just ninth in the league. Kyle Seager also made it onto my ballot on the strength of 8 fielding runs, and Francisco Lindor came close with 5 from baserunning and 10 from fielding. David Ortiz and Miguel Cabrera gave up 5 runs from non-hitting activities (or in Ortiz’s case, non-acitivty), which pushed them just off the ballot. Last year’s Player B, Josh Donaldson, was only a hair behind Betts, having another excellent season with 65 RAR and good-average fielding except in FRAA, which didn’t like his performance at all (-12).

The AL starting pitchers lacked any standout Cy Young candidates, but made up for it by being tightly bunched, so four of the final six spots go to them:

1. CF Mike Trout, LAA
2. 2B Jose Altuve, HOU
3. RF Mookie Betts, BOS
4. 3B Josh Donaldson, TOR
5. SP Justin Verlander, DET
6. 2B Robinson Cano, NYA
7. SP Rick Porcello, BOS
8. SP Chris Sale, CHA
9. SP Corey Kluber, CLE
10. 3B Kyle Seager, SEA

In the NL, I think Kris Bryant is a pretty clear pick for the top spot. He was second in the league in RAR by just one run to Joey Votto, which he makes up with baserunning alone and pads with strong fielding runs (2, 10, 12). Anthony Rizzo seems to be the other top candidate in mainstream opinion, but he only ranks third among first baseman on my ballot. Rizzo, Freddie Freeman, and Joey Votto all had similar playing time, but both significantly outhit him (Rizzo 6.9 RG, Votto 8.2, Freeman 7.6). Rizzo makes up much of the ground on Votto with his glove, but Freeman is no slouch himself.

Corey Seager got mixed reviews as a fielder (-8, 0, 11) so he falls just behind Freeman on my ballot. I’m quite certain I’ve never had brothers on both of my MVP top 10s in the same year, or any year. Daniel Murphy was third to Votto and Bryant in RAR, but his fielding reviews aren’t so mixed (-5, -11, -6), and even before considering that was actually just behind Max Scherzer in RAR. From there, it’s just a matter of mixing in the pitchers and noting that four Cubs are on the ballot:

1. 3B Kris Bryant, CHN
2. 1B Freddie Freeman, ATL
3. SS Corey Seager, LA
4. SP Max Scherzer, WAS
5. 2B Daniel Murphy, WAS
6. SP Jon Lester, CHN
7. 1B Joey Votto, CIN
8. 1B Anthony Rizzo, CHN
9. SP Kyle Hendicks, CHN
10. SP Clayton Kershaw, LA

Hypothetical Ballot: Rookie of the Year

It was a bad year for rookies in the AL, made more interesting by the very late arrival of Gary Sanchez. Most of the discussion about the award seems to center around whether it is appropriate to give it to Sanchez based on his brilliant 227 PA, and whether ROY should be a value award, a future prospect award, or some kind of ungodly hybrid of the two. My own approach is that it should be a value award--anyone who is a rookie should be eligible and my primary criteria is how productive they were in 2016, not how old they are, their prospect pedigree, how their team held down their service time, or the like. Only in a very close decision would I factor in those criteria. I understand why others might consider those factors, and why it makes a lot more sense to deviate from a value approach for ROY than for Cy Young or MVP.

As such, I don’t consider Sanchez’s case to be particularly compelling. Yes, Sanchez was more productive on a rate basis than any AL hitter other than Mike Trout. Yes, the lack of a standout candidate in the rest of the league makes Sanchez all the more appealing. But Sanchez’s performance far outpaced both his prospect status and his minor league numbers (807 OPS in 313 PA at AAA this year, 815 across AA and AAA last year). If I was going to consider a shooting star exception, it would be for someone who checked all the boxes. I would much rather have Sanchez’s future than any of the other four players on my ballot, but in 2016 he fell in the middle in terms of value.

With Sanchez out, the top of the ballot comes down to Michael Fulmer, who is the top non-Sanchez candidate in the popular discussion, and Chris Devenski. I watched a game in which Devenski pitched this year and was vaguely aware of his existence in subsequent box scores, but how effectively he was pitching completely escaped my attention until I put together my annual stat reports. Devenski pitched extremely well for Houston, mostly in relief (48 games, 5 starts) with a 1.80 RRA over 108 innings. His peripherals were strong as well (2.39 eRA and 2.79 dRA).

Fulmer pitched 159 innings with a 3.41 RRA for 42 RAR versus Devenski’s 39. Fulmer’s peripherals were also reasonably strong (3.46 eRA, 4.02 dRA), and since this was a curious case I also checked Baseball Prospectus’ DRA, which attempts to normalize for any number of relevant variables (park, umpires, defensive support, framing, quality of opposition, etc.). Using DRA, Fulmer has a clear edge considering his quantity advantage (3.49 to 3.72).

One thing my RAR figures oversimplify is pitcher’s roles--it is a binary reliever (with replacement level at 111% of league average) or start (replacement level 128% of league average). If I figured RAR using Devenski’s inning split to set his replacement level (83 innings in relief to 24 starting works out to 115% of league as the replacement level), his RAR would edge up to 41. It should be noted too that Devenski pitched decently in his five starts, averaging just under 5 innings with a 4.01 RA.

I think the two are very close; this is a case where Fulmer’s status as a starter and a younger, better regarded prospect leave him just ahead for me. Even so, I assume Devenski will rank higher on my ballot than almost any submitted even for the IBAs.

Filling out the bottom of the ballot, the only other legitimate hitting candidate, Tyler Naquin and his 26 RAR, was heavily platooned and fares poorly in defensive metrics. That leaves two A’s pitchers, one a starter and one a reliever. If I strictly followed RAR, I would actually have the latter (Ryan Dull) ahead of the former (Sean Manaea), and the peripherals don’t really help either’s case, but since they were so close I will vote here for prospect status.

1. SP Michael Fulmer, DET
2. RP Chris Devenski, HOU
3. C Gary Sanchez, NYA
4. SP Sean Manaea, OAK
5. RP Ryan Dull, OAK

The top of the NL ballot is easy, as Corey Seager is a legitimate MVP candidate and far outshines the rest of the rookies. There is a cluster of qualified candidates in the 30-40 RAR range who make up the rest of my ballot. Kenta Maeda gets the nod over Junior Guerra as top pitcher based on stronger peripherals, with apologies to Zach Davies, Tyler Anderson, and Steven Matz. Among hitters, Aledmys Diaz led in RAR with 37 to Trea Turner’s 34, but Diaz’s fielding metrics are bad (-9 FRAA, -3 DRS, -8 UZR) while Turner’s are…not as bad (-3, -2, -5). Both are credited with baserunning value beyond their steals by BP (2 runs for Diaz, 4 for Turner); when you add it up it’s very close, but I consider Turner’s age and the fact that he did it in 130 PA to put him ahead:

1. SS Corey Seager, LA
2. SP Kenta Maeda, LA
3. SP Junior Guerra, MIL
4. CF Trea Turner, WAS
5. SS Aledmys Diaz, STL

End of Season Statistics, 2016

The spreadsheets are published as Google Spreadsheets, which you can download in Excel format by changing the extension in the address from "=html" to "=xls". That way you can download them and manipulate things however you see fit.

The data comes from a number of different sources. Most of the data comes from Baseball-Reference. KJOK's park database is extremely helpful in determining when park factors should reset. Data on bequeathed runners for relievers comes from Baseball Prospectus.

The basic philosophy behind these stats is to use the simplest methods that have acceptable accuracy. Of course, "acceptable" is in the eye of the beholder, namely me. I use Pythagenpat not because other run/win converters, like a constant RPW or a fixed exponent are not accurate enough for this purpose, but because it's mine and it would be kind of odd if I didn't use it.

If I seem to be a stickler for purity in my critiques of others' methods, I'd contend it is usually in a theoretical sense, not an input sense. So when I exclude hit batters, I'm not saying that hit batters are worthless or that they *should* be ignored; it's just easier not to mess with them and not that much less accurate.

I also don't really have a problem with people using sub-standard methods (say, Basic RC) as long as they acknowledge that they are sub-standard. If someone pretends that Basic RC doesn't undervalue walks or cause problems when applied to extreme individuals, I'll call them on it; if they explain its shortcomings but use it regardless, I accept that. Take these last three paragraphs as my acknowledgment that some of the statistics displayed here have shortcomings as well, and I've at least attempted to describe some of them in the discussion below.

The League spreadsheet is pretty straightforward--it includes league totals and averages for a number of categories, most or all of which are explained at appropriate junctures throughout this piece. The advent of interleague play has created two different sets of league totals--one for the offense of league teams and one for the defense of league teams. Before interleague play, these two were identical. I do not present both sets of totals (you can figure the defensive ones yourself from the team spreadsheet, if you desire), just those for the offenses. The exception is for the defense-specific statistics, like innings pitched and quality starts. The figures for those categories in the league report are for the defenses of the league's teams. However, I do include each league's breakdown of basic pitching stats between starters and relievers (denoted by "s" or "r" prefixes), and so summing those will yield the totals from the pitching side. The one abbreviation you might not recognize is "N"--this is the league average of runs/game for one team, and it will pop up again.

The Team spreadsheet focuses on overall team performance--wins, losses, runs scored, runs allowed. The columns included are: Park Factor (PF), Home Run Park Factor (PFhr), Winning Percentage (W%), Expected W% (EW%), Predicted W% (PW%), wins, losses, runs, runs allowed, Runs Created (RC), Runs Created Allowed (RCA), Home Winning Percentage (HW%), Road Winning Percentage (RW%) [exactly what they sound like--W% at home and on the road], Runs/Game (R/G), Runs Allowed/Game (RA/G), Runs Created/Game (RCG), Runs Created Allowed/Game (RCAG), and Runs Per Game (the average number of runs scored an allowed per game). Ideally, I would use outs as the denominator, but for teams, outs and games are so closely related that I don’t think it’s worth the extra effort.

The runs and Runs Created figures are unadjusted, but the per-game averages are park-adjusted, except for RPG which is also raw. Runs Created and Runs Created Allowed are both based on a simple Base Runs formula. The formula is:

A = H + W - HR - CS
B = (2TB - H - 4HR + .05W + 1.5SB)*.76
C = AB - H
D = HR
Naturally, A*B/(B + C) + D.

I have explained the methodology used to figure the PFs before, but the cliff’s notes version is that they are based on five years of data when applicable, include both runs scored and allowed, and they are regressed towards average (PF = 1), with the amount of regression varying based on the number of years of data used. There are factors for both runs and home runs. The initial PF (not shown) is:

iPF = (H*T/(R*(T - 1) + H) + 1)/2
where H = RPG in home games, R = RPG in road games, T = # teams in league (14 for AL and 16 for NL). Then the iPF is converted to the PF by taking x*iPF + (1-x), where x = .6 if one year of data is used, .7 for 2, .8 for 3, and .9 for 4+.

It is important to note, since there always seems to be confusion about this, that these park factors already incorporate the fact that the average player plays 50% on the road and 50% at home. That is what the adding one and dividing by 2 in the iPF is all about. So if I list Fenway Park with a 1.02 PF, that means that it actually increases RPG by 4%.

In the calculation of the PFs, I did not get picky and take out “home” games that were actually at neutral sites.

There are also Team Offense and Defense spreadsheets. These include the following categories:

Team offense: Plate Appearances, Batting Average (BA), On Base Average (OBA), Slugging Average (SLG), Secondary Average (SEC), Walks and Hit Batters per At Bat (WAB), Isolated Power (SLG - BA), R/G at home (hR/G), and R/G on the road (rR/G) BA, OBA, SLG, WAB, and ISO are park-adjusted by dividing by the square root of park factor (or the equivalent; WAB = (OBA - BA)/(1 - OBA), ISO = SLG - BA, and SEC = WAB + ISO).

Team defense: Innings Pitched, BA, OBA, SLG, Innings per Start (IP/S), Starter's eRA (seRA), Reliever's eRA (reRA), Quality Start Percentage (QS%), RA/G at home (hRA/G), RA/G on the road (rRA/G), Battery Mishap Rate (BMR), Modified Fielding Average (mFA), and Defensive Efficiency Record (DER). BA, OBA, and SLG are park-adjusted by dividing by the square root of PF; seRA and reRA are divided by PF.

The three fielding metrics I've included are limited it only to metrics that a) I can calculate myself and b) are based on the basic available data, not specialized PBP data. The three metrics are explained in this post, but here are quick descriptions of each:

1) BMR--wild pitches and passed balls per 100 baserunners = (WP + PB)/(H + W - HR)*100

2) mFA--fielding average removing strikeouts and assists = (PO - K)/(PO - K + E)

3) DER--the Bill James classic, using only the PA-based estimate of plays made. Based on a suggestion by Terpsfan101, I've tweaked the error coefficient. Plays Made = PA - K - H - W - HR - HB - .64E and DER = PM/(PM + H - HR + .64E)

Next are the individual player reports. I defined a starting pitcher as one with 15 or more starts. All other pitchers are eligible to be included as a reliever. If a pitcher has 40 appearances, then they are included. Additionally, if a pitcher has 50 innings and less than 50% of his appearances are starts, he is also included as a reliever (this allows some swingmen type pitchers who wouldn’t meet either the minimum start or appearance standards to get in).

For all of the player reports, ages are based on simply subtracting their year of birth from 2016. I realize that this is not compatible with how ages are usually listed and so “Age 27” doesn’t necessarily correspond to age 27 as I list it, but it makes everything a heckuva lot easier, and I am more interested in comparing the ages of the players to their contemporaries than fitting them into historical studies, and for the former application it makes very little difference. The "R" category records rookie status with a "R" for rookies and a blank for everyone else; I've trusted Baseball Prospectus on this. Also, all players are counted as being on the team with whom they played/pitched (IP or PA as appropriate) the most.

For relievers, the categories listed are: Games, Innings Pitched, estimated Plate Appearances (PA), Run Average (RA), Relief Run Average (RRA), Earned Run Average (ERA), Estimated Run Average (eRA), DIPS Run Average (dRA), Strikeouts per Game (KG), Walks per Game (WG), Guess-Future (G-F), Inherited Runners per Game (IR/G), Batting Average on Balls in Play (%H), Runs Above Average (RAA), and Runs Above Replacement (RAR).

IR/G is per relief appearance (G - GS); it is an interesting thing to look at, I think, in lieu of actual leverage data. You can see which closers come in with runners on base, and which are used nearly exclusively to start innings. Of course, you can’t infer too much; there are bad relievers who come in with a lot of people on base, not because they are being used in high leverage situations, but because they are long men being used in low-leverage situations already out of hand.

For starting pitchers, the columns are: Wins, Losses, Innings Pitched, Estimated Plate Appearances (PA), RA, RRA, ERA, eRA, dRA, KG, WG, G-F, %H, Pitches/Start (P/S), Quality Start Percentage (QS%), RAA, and RAR. RA and ERA you know--R*9/IP or ER*9/IP, park-adjusted by dividing by PF. The formulas for eRA and dRA are based on the same Base Runs equation and they estimate RA, not ERA.

* eRA is based on the actual results allowed by the pitcher (hits, doubles, home runs, walks, strikeouts, etc.). It is park-adjusted by dividing by PF.

* dRA is the classic DIPS-style RA, assuming that the pitcher allows a league average %H, and that his hits in play have a league-average S/D/T split. It is park-adjusted by dividing by PF.

The formula for eRA is:

A = H + W - HR
B = (2*TB - H - 4*HR + .05*W)*.78
C = AB - H = K + (3*IP - K)*x (where x is figured as described below for PA estimation and is typically around .93) = PA (from below) - H - W
eRA = (A*B/(B + C) + HR)*9/IP

To figure dRA, you first need the estimate of PA described below. Then you calculate W, K, and HR per PA (call these %W, %K, and %HR). Percentage of balls in play (BIP%) = 1 - %W - %K - %HR. This is used to calculate the DIPS-friendly estimate of %H (H per PA) as e%H = Lg%H*BIP%.

Now everything has a common denominator of PA, so we can plug into Base Runs:

A = e%H + %W
B = (2*(z*e%H + 4*%HR) - e%H - 5*%HR + .05*%W)*.78
C = 1 - e%H - %W - %HR
cRA = (A*B/(B + C) + %HR)/C*a

z is the league average of total bases per non-HR hit (TB - 4*HR)/(H - HR), and a is the league average of (AB - H) per game.

In the past I presented a couple of batted ball RA estimates. I’ve removed these, not just because batted ball data exhibits questionable reliability but because these metrics were complicated to figure, required me to collate the batted ball data, and were not personally useful to me. I figure these stats for my own enjoyment and have in some form or another going back to 1997. I share them here only because I would do it anyway, so if I’m not interested in certain categories, there’s no reason to keep presenting them.

Instead, I’m showing strikeout and walk rate, both expressed as per game. By game I mean not nine innings but rather the league average of PA/G. I have always been a proponent of using PA and not IP as the denominator for non-run pitching rates, and now the use of per PA rates is widespread. Usually these are expressed as K/PA and W/PA, or equivalently, percentage of PA with a strikeout or walk. I don’t believe that any site publishes these as K and W per equivalent game as I am here. This is not better than K%--it’s simply applying a scalar multiplier. I like it because it generally follows the same scale as the familiar K/9.

To facilitate this, I’ve finally corrected a flaw in the formula I use to estimate plate appearances for pitchers. Previously, I’ve done it the lazy way by not splitting strikeouts out from other outs. I am now using this formula to estimate PA (where PA = AB + W):

PA = K + (3*IP - K)*x + H + W
Where x = league average of (AB - H - K)/(3*IP - K)

Then KG = K*Lg(PA/G) and WG = W*Lg(PA/G).

G-F is a junk stat, included here out of habit because I've been including it for years. It was intended to give a quick read of a pitcher's expected performance in the next season, based on eRA and strikeout rate. Although the numbers vaguely resemble RAs, it's actually unitless. As a rule of thumb, anything under four is pretty good for a starter. G-F = 4.46 + .095(eRA) - .113(K*9/IP). It is a junk stat. JUNK STAT JUNK STAT JUNK STAT. Got it?

%H is BABIP, more or less--%H = (H - HR)/(PA - HR - K - W), where PA was estimated above. Pitches/Start includes all appearances, so I've counted relief appearances as one-half of a start (P/S = Pitches/(.5*G + .5*GS). QS% is just QS/(G - GS); I don't think it's particularly useful, but Doug's Stats include QS so I include it.

I've used a stat called Relief Run Average (RRA) in the past, based on Sky Andrecheck's article in the August 1999 By the Numbers; that one only used inherited runners, but I've revised it to include bequeathed runners as well, making it equally applicable to starters and relievers. I use RRA as the building block for baselined value estimates for all pitchers. I explained RRA in this article, but the bottom line formulas are:

BRSV = BRS - BR*i*sqrt(PF)
IRSV = IR*i*sqrt(PF) - IRS
RRA = ((R - (BRSV + IRSV))*9/IP)/PF

The two baselined stats are Runs Above Average (RAA) and Runs Above Replacement (RAR). Starting in 2015 I revised RAA to use a slightly different baseline for starters and relievers as described here. The adjustment is based on patterns from the last several seasons of league average starter and reliever eRA. Thus it does not adjust for any advantages relief pitchers enjoy that are not reflected in their component statistics. This could include runs allowed scoring rules that benefit relievers (although the use of RRA should help even the scales in this regard, at least compared to raw RA) and the talent advantage of starting pitchers. The RAR baselines do attempt to take the latter into account, and so the difference in starter and reliever RAR will be more stark than the difference in RAA.

RAA (relievers) = (.951*LgRA - RRA)*IP/9
RAA (starters) = (1.025*LgRA - RRA)*IP/9
RAR (relievers) = (1.11*LgRA - RRA)*IP/9
RAR (starters) = (1.28*LgRA - RRA)*IP/9

All players with 250 or more plate appearances (official, total plate appearances) are included in the Hitters spreadsheets (along with some players close to the cutoff point who I was interested in). Each is assigned one position, the one at which they appeared in the most games. The statistics presented are: Games played (G), Plate Appearances (PA), Outs (O), Batting Average (BA), On Base Average (OBA), Slugging Average (SLG), Secondary Average (SEC), Runs Created (RC), Runs Created per Game (RG), Speed Score (SS), Hitting Runs Above Average (HRAA), Runs Above Average (RAA), Hitting Runs Above Replacement (HRAR), and Runs Above Replacement (RAR).

Starting in 2015, I'm including hit batters in all related categories for hitters, so PA is now equal to AB + W+ HB. Outs are AB - H + CS. BA and SLG you know, but remember that without SF, OBA is just (H + W + HB)/(AB + W + HB). Secondary Average = (TB - H + W + HB)/AB = SLG - BA + (OBA - BA)/(1 - OBA). I have not included net steals as many people (and Bill James himself) do, but I have included HB which some do not.

BA, OBA, and SLG are park-adjusted by dividing by the square root of PF. This is an approximation, of course, but I'm satisfied that it works well (I plan to post a couple articles on this some time during the offseason). The goal here is to adjust for the win value of offensive events, not to quantify the exact park effect on the given rate. I use the BA/OBA/SLG-based formula to figure SEC, so it is park-adjusted as well.

Runs Created is actually Paul Johnson's ERP, more or less. Ideally, I would use a custom linear weights formula for the given league, but ERP is just so darn simple and close to the mark that it’s hard to pass up. I still use the term “RC” partially as a homage to Bill James (seriously, I really like and respect him even if I’ve said negative things about RC and Win Shares), and also because it is just a good term. I like the thought put in your head when you hear “creating” a run better than “producing”, “manufacturing”, “generating”, etc. to say nothing of names like “equivalent” or “extrapolated” runs. None of that is said to put down the creators of those methods--there just aren’t a lot of good, unique names available.

For 2015, I refined the formula a little bit to:

1. include hit batters at a value equal to that of a walk
2. value intentional walks at just half the value of a regular walk
3. recalibrate the multiplier based on the last ten major league seasons (2005-2014)

This revised RC = (TB + .8H + W + HB - .5IW + .7SB - CS - .3AB)*.310

RC is park adjusted by dividing by PF, making all of the value stats that follow park adjusted as well. RG, the Runs Created per Game rate, is RC/O*25.5. I do not believe that outs are the proper denominator for an individual rate stat, but I also do not believe that the distortions caused are that bad. (I still intend to finish my rate stat series and discuss all of the options in excruciating detail, but alas you’ll have to take my word for it now).

Several years ago I switched from using my own "Speed Unit" to a version of Bill James' Speed Score; of course, Speed Unit was inspired by Speed Score. I only use four of James' categories in figuring Speed Score. I actually like the construct of Speed Unit better as it was based on z-scores in the various categories (and amazingly a couple other sabermetricians did as well), but trying to keep the estimates of standard deviation for each of the categories appropriate was more trouble than it was worth.

Speed Score is the average of four components, which I'll call a, b, c, and d:

a = ((SB + 3)/(SB + CS + 7) - .4)*20
b = sqrt((SB + CS)/(S + W))*14.3
c = ((R - HR)/(H + W - HR) - .1)*25
d = T/(AB - HR - K)*450

James actually uses a sliding scale for the triples component, but it strikes me as needlessly complex and so I've streamlined it. He looks at two years of data, which makes sense for a gauge that is attempting to capture talent and not performance, but using multiple years of data would be contradictory to the guiding principles behind this set of reports (namely, simplicity. Or laziness. You're pick.) I also changed some of his division to mathematically equivalent multiplications.

There are a whopping four categories that compare to a baseline; two for average, two for replacement. Hitting RAA compares to a league average hitter; it is in the vein of Pete Palmer’s Batting Runs. RAA compares to an average hitter at the player’s primary position. Hitting RAR compares to a “replacement level” hitter; RAR compares to a replacement level hitter at the player’s primary position. The formulas are:

HRAA = (RG - N)*O/25.5
RAA = (RG - N*PADJ)*O/25.5
HRAR = (RG - .73*N)*O/25.5
RAR = (RG - .73*N*PADJ)*O/25.5

PADJ is the position adjustment, and it is based on 2002-2011 offensive data. For catchers it is .89; for 1B/DH, 1.17; for 2B, .97; for 3B, 1.03; for SS, .93; for LF/RF, 1.13; and for CF, 1.02. I had been using the 1992-2001 data as a basis for some time, but finally updated for 2012. I’m a little hesitant about this update, as the middle infield positions are the biggest movers (higher positional adjustments, meaning less positional credit). I have no qualms for second base, but the shortstop PADJ is out of line with the other position adjustments widely in use and feels a bit high to me. But there are some decent points to be made in favor of offensive adjustments, and I’ll have a bit more on this topic in general below.

That was the mechanics of the calculations; now I'll twist myself into knots trying to justify them. If you only care about the how and not the why, stop reading now.

The first thing that should be covered is the philosophical position behind the statistics posted here. They fall on the continuum of ability and value in what I have called "performance". Performance is a technical-sounding way of saying "Whatever arbitrary combination of ability and value I prefer".

With respect to park adjustments, I am not interested in how any particular player is affected, so there is no separate adjustment for lefties and righties for instance. The park factor is an attempt to determine how the park affects run scoring rates, and thus the win value of runs.

I apply the park factor directly to the player's statistics, but it could also be applied to the league context. The advantage to doing it my way is that it allows you to compare the component statistics (like Runs Created or OBA) on a park-adjusted basis. The drawback is that it creates a new theoretical universe, one in which all parks are equal, rather than leaving the player grounded in the actual context in which he played and evaluating how that context (and not the player's statistics) was altered by the park.

The good news is that the two approaches are essentially equivalent; in fact, they are precisely equivalent if you assume that the Runs Per Win factor is equal to the RPG. Suppose that we have a player in an extreme park (PF = 1.15, approximately like Coors Field pre-humidor) who has an 8 RG before adjusting for park, while making 350 outs in a 4.5 N league. The first method of park adjustment, the one I use, converts his value into a neutral park, so his RG is now 8/1.15 = 6.957. We can now compare him directly to the league average:

RAA = (6.957 - 4.5)*350/25.5 = +33.72

The second method would be to adjust the league context. If N = 4.5, then the average player in this park will create 4.5*1.15 = 5.175 runs. Now, to figure RAA, we can use the unadjusted RG of 8:

RAA = (8 - 5.175)*350/25.5 = +38.77

These are not the same, as you can obviously see. The reason for this is that they take place in two different contexts. The first figure is in a 9 RPG (2*4.5) context; the second figure is in a 10.35 RPG (2*4.5*1.15) context. Runs have different values in different contexts; that is why we have RPW converters in the first place. If we convert to WAA (using RPW = RPG, which is only an approximation, so it's usually not as tidy as it appears below), then we have:

WAA = 33.72/9 = +3.75
WAA = 38.77/10.35 = +3.75

Once you convert to wins, the two approaches are equivalent. The other nice thing about the first approach is that once you park-adjust, everyone in the league is in the same context, and you can dispense with the need for converting to wins at all. You still might want to convert to wins, and you'll need to do so if you are comparing the 2015 players to players from other league-seasons (including between the AL and NL in the same year), but if you are only looking to compare Jose Bautista to Miguel Cabrera, it's not necessary. WAR is somewhat ubiquitous now, but personally I prefer runs when possible--why mess with decimal points if you don't have to?

The park factors used to adjust player stats here are run-based. Thus, they make no effort to project what a player "would have done" in a neutral park, or account for the difference effects parks have on specific events (walks, home runs, BA) or types of players. They simply account for the difference in run environment that is caused by the park (as best I can measure it). As such, they don't evaluate a player within the actual run context of his team's games; they attempt to restate the player's performance as an equivalent performance in a neutral park.

I suppose I should also justify the use of sqrt(PF) for adjusting component statistics. The classic defense given for this approach relies on basic Runs Created--runs are proportional to OBA*SLG, and OBA*SLG/PF = OBA/sqrt(PF)*SLG/sqrt(PF). While RC may be an antiquated tool, you will find that the square root adjustment is fairly compatible with linear weights or Base Runs as well. I am not going to take the space to demonstrate this claim here, but I will some time in the future.

Many value figures published around the sabersphere adjust for the difference in quality level between the AL and NL. I don't, but this is a thorny area where there is no right or wrong answer as far as I'm concerned. I also do not make an adjustment in the league averages for the fact that the overall NL averages include pitcher batting and the AL does not (not quite true in the era of interleague play, but you get my drift).

The difference between the leagues may not be precisely calculable, and it certainly is not constant, but it is real. If the average player in the AL is better than the average player in the NL, it is perfectly reasonable to expect the average AL player to have more RAR than the average NL player, and that will not happen without some type of adjustment. On the other hand, if you are only interested in evaluating a player relative to his own league, such an adjustment is not necessarily welcome.

The league argument only applies cleanly to metrics baselined to average. Since replacement level compares the given player to a theoretical player that can be acquired on the cheap, the same pool of potential replacement players should by definition be available to the teams of each league. One could argue that if the two leagues don't have equal talent at the major league level, they might not have equal access to replacement level talent--except such an argument is at odds with the notion that replacement level represents talent that is truly "freely available".

So it's hard to justify the approach I take, which is to set replacement level relative to the average runs scored in each league, with no adjustment for the difference in the leagues. The best justification is that it's simple and it treats each league as its own universe, even if in reality they are connected.

The replacement levels I have used here are very much in line with the values used by other sabermetricians. This is based both on my own "research", my interpretation of other's people research, and a desire to not stray from consensus and make the values unhelpful to the majority of people who may encounter them.

Replacement level is certainly not settled science. There is always going to be room to disagree on what the baseline should be. Even if you agree it should be "replacement level", any estimate of where it should be set is just that--an estimate. Average is clean and fairly straightforward, even if its utility is questionable; replacement level is inherently messy. So I offer the average baseline as well.

For position players, replacement level is set at 73% of the positional average RG (since there's a history of discussing replacement level in terms of winning percentages, this is roughly equivalent to .350). For starting pitchers, it is set at 128% of the league average RA (.380), and for relievers it is set at 111% (.450).

I am still using an analytical structure that makes the comparison to replacement level for a position player by applying it to his hitting statistics. This is the approach taken by Keith Woolner in VORP (and some other earlier replacement level implementations), but the newer metrics (among them Rally and Fangraphs' WAR) handle replacement level by subtracting a set number of runs from the player's total runs above average in a number of different areas (batting, fielding, baserunning, positional value, etc.), which for lack of a better term I will call the subtraction approach.

The offensive positional adjustment makes the inherent assumption that the average player at each position is equally valuable. I think that this is close to being true, but it is not quite true. The ideal approach would be to use a defensive positional adjustment, since the real difference between a first baseman and a shortstop is their defensive value. When you bat, all runs count the same, whether you create them as a first baseman or as a shortstop.

That being said, using "replacement hitter at position" does not cause too many distortions. It is not theoretically correct, but it is practically powerful. For one thing, most players, even those at key defensive positions, are chosen first and foremost for their offense. Empirical research by Keith Woolner has shown that the replacement level hitting performance is about the same for every position, relative to the positional average.

Figuring what the defensive positional adjustment should be, though, is easier said than done. Therefore, I use the offensive positional adjustment. So if you want to criticize that choice, or criticize the numbers that result, be my guest. But do not claim that I am holding this up as the correct analytical structure. I am holding it up as the most simple and straightforward structure that conforms to reality reasonably well, and because while the numbers may be flawed, they are at least based on an objective formula that I can figure myself. If you feel comfortable with some other assumptions, please feel free to ignore mine.

That still does not justify the use of HRAR--hitting runs above replacement--which compares each hitter, regardless of position, to 73% of the league average. Basically, this is just a way to give an overall measure of offensive production without regard for position with a low baseline. It doesn't have any real baseball meaning.

A player who creates runs at 90% of the league average could be above-average (if he's a shortstop or catcher, or a great fielder at a less important fielding position), or sub-replacement level (DHs that create 3.5 runs per game are not valuable properties). Every player is chosen because his total value, both hitting and fielding, is sufficient to justify his inclusion on the team. HRAR fails even if you try to justify it with a thought experiment about a world in which defense doesn't matter, because in that case the absolute replacement level (in terms of RG, without accounting for the league average) would be much higher than it is currently.

The specific positional adjustments I use are based on 2002-2011 data. I stick with them because I have not seen compelling evidence of a change in the degree of difficulty or scarcity between the positions between now and then, and because I think they are fairly reasonable. The positions for which they diverge the most from the defensive position adjustments in common use are 2B, 3B, and CF. Second base is considered a premium position by the offensive PADJ (.97), while third base and center field have similar adjustments in the opposite direction (1.03 and 1.02).

Another flaw is that the PADJ is applied to the overall league average RG, which is artificially low for the NL because of pitcher's batting. When using the actual league average runs/game, it's tough to just remove pitchers--any adjustment would be an estimate. If you use the league total of runs created instead, it is a much easier fix.

One other note on this topic is that since the offensive PADJ is a stand-in for average defensive value by position, ideally it would be applied by tying it to defensive playing time. I have done it by outs, though.

The reason I have taken this flawed path is because 1) it ties the position adjustment directly into the RAR formula rather than leaving it as something to subtract on the outside and more importantly 2) there’s no straightforward way to do it. The best would be to use defensive innings--set the full-time player to X defensive innings, figure how Derek Jeter’s innings compared to X, and adjust his PADJ accordingly. Games in the field or games played are dicey because they can cause distortion for defensive replacements. Plate Appearances avoid the problem that outs have of being highly related to player quality, but they still carry the illogic of basing it on offensive playing time. And of course the differences here are going to be fairly small (a few runs). That is not to say that this way is preferable, but it’s not horrible either, at least as far as I can tell.

To compare this approach to the subtraction approach, start by assuming that a replacement level shortstop would create .86*.73*4.5 = 2.825 RG (or would perform at an overall level of equivalent value to being an average fielder at shortstop while creating 2.825 runs per game). Suppose that we are comparing two shortstops, each of whom compiled 600 PA and played an equal number of defensive games and innings (and thus would have the same positional adjustment using the subtraction approach). Alpha made 380 outs and Bravo made 410 outs, and each ranked as dead-on average in the field.

The difference in overall RAR between the two using the subtraction approach would be equal to the difference between their offensive RAA compared to the league average. Assuming the league average is 4.5 runs, and that both Alpha and Bravo created 75 runs, their offensive RAAs are:

Alpha = (75*25.5/380 - 4.5)*380/25.5 = +7.94

Similarly, Bravo is at +2.65, and so the difference between them will be 5.29 RAR.

Using the flawed approach, Alpha's RAR will be:

(75*25.5/380 - 4.5*.73*.86)*380/25.5 = +32.90

Bravo's RAR will be +29.58, a difference of 3.32 RAR, which is two runs off of the difference using the subtraction approach.

The downside to using PA is that you really need to consider park effects if you do, whereas outs allow you to sidestep park effects. Outs are constant; plate appearances are linked to OBA. Thus, they not only depend on the offensive context (including park factor), but also on the quality of one's team. Of course, attempting to adjust for team PA differences opens a huge can of worms which is not really relevant; for now, the point is that using outs for individual players causes distortions, sometimes trivial and sometimes bothersome, but almost always makes one's life easier.

I do not include fielding (or baserunning outside of steals, although that is a trivial consideration in comparison) in the RAR figures--they cover offense and positional value only). This in no way means that I do not believe that fielding is an important consideration in player evaluation. However, two of the key principles of these stat reports are 1) not incorporating any data that is not readily available and 2) not simply including other people's results (of course I borrow heavily from other people's methods, but only adapting methodology that I can apply myself).

Any fielding metric worth its salt will fail to meet either criterion--they use zone data or play-by-play data which I do not have easy access to. I do not have a fielding metric that I have stapled together myself, and so I would have to simply lift other analysts' figures.

Setting the practical reason for not including fielding aside, I do have some reservations about lumping fielding and hitting value together in one number because of the obvious differences in reliability between offensive and fielding metrics. In theory, they absolutely should be put together. But in practice, I believe it would be better to regress the fielding metric to a point at which it would be roughly equivalent in reliability to the offensive metric.

Offensive metrics have error bars associated with them, too, of course, and in evaluating a single season's value, I don't care about the vagaries that we often lump together as "luck". Still, there are errors in our assessment of linear weight values and players that collect an unusual proportion of infield hits or hits to the left side, errors in estimation of park factor, and any number of other factors that make their events more or less valuable than an average event of that type.

Fielding metrics offer up all of that and more, as we cannot be nearly as certain of true successes and failures as we are when analyzing offense. Recent investigations, particularly by Colin Wyers, have raised even more questions about the level of uncertainty. So, even if I was including a fielding value, my approach would be to assume that the offensive value was 100% reliable (which it isn't), and regress the fielding metric relative to that (so if the offensive metric was actually 70% reliable, and the fielding metric 40% reliable, I'd treat the fielding metric as .4/.7 = 57% reliable when tacking it on, to illustrate with a simplified and completely made up example presuming that one could have a precise estimate of nebulous "reliability").

Given the inherent assumption of the offensive PADJ that all positions are equally valuable, once RAR has been figured for a player, fielding value can be accounted for by adding on his runs above average relative to a player at his own position. If there is a shortstop that is -2 runs defensively versus an average shortstop, he is without a doubt a plus defensive player, and a more valuable defensive player than a first baseman who was +1 run better than an average first baseman. Regardless, since it was implicitly assumed that they are both average defensively for their position when RAR was calculated, the shortstop will see his value docked two runs. This DOES NOT MEAN that the shortstop has been penalized for his defense. The whole process of accounting for positional differences, going from hitting RAR to positional RAR, has benefited him.

I've found that there is often confusion about the treatment of first baseman and designated hitters in my PADJ methodology, since I consider DHs as in the same pool as first baseman. The fact of the matter is that first baseman outhit DH. There are any number of potential explanations for this; DHs are often old or injured, players hit worse when DHing than they do when playing the field, etc. This actually helps first baseman, since the DHs drag the average production of the pool down, thus resulting in a lower replacement level than I would get if I considered first baseman alone.

However, this method does assume that a 1B and a DH have equal defensive value. Obviously, a DH has no defensive value. What I advocate to correct this is to treat a DH as a bad defensive first baseman, and thus knock another five or so runs off of his RAR for a full-time player. I do not incorporate this into the published numbers, but you should keep it in mind. However, there is no need to adjust the figures for first baseman upwards --the only necessary adjustment is to take the DHs down a notch.

Finally, I consider each player at his primary defensive position (defined as where he appears in the most games), and do not weight the PADJ by playing time. This does shortchange a player like Ben Zobrist (who saw significant time at a tougher position than his primary position), and unduly boost a player like Buster Posey (who logged a lot of games at a much easier position than his primary position). For most players, though, it doesn't matter much. I find it preferable to make manual adjustments for the unusual cases rather than add another layer of complexity to the whole endeavor.

2016 League

2016 Park Factors

2016 Team

2016 Team Offense

2016 Team Defense

2016 AL Relievers

2016 NL Relievers

2016 AL Starters

2016 NL Starters

2016 AL Hitters

2016 NL Hitters

Crude Playoff Odds--2016

These are very simple playoff odds, based on my crude rating system for teams using an equal mix of W%, EW% (based on R/RA), PW% (based on RC/RCA), and 69 games of .500. They account for home field advantage by assuming a .500 team wins 54.2% of home games (major league average 2006-2015). They assume that a team's inherent strength is constant from game-to-game. They do not generally account for any number of factors that you would actually want to account for if you were serious about this, including but not limited to injuries, the current construction of the team rather than the aggregate seasonal performance, pitching rotations, estimated true talent of the players, etc.

I say “generally” since this year, the team I am a fan of (Cleveland) lost two key starting pitchers, and I wanted to account for that in the ratings. While other teams have injuries of note as well, I did not consider those. This approach is basically being as conservative as reasonably possible in estimating the Indians strength. Using a runs allowed approach (and not adjusting for bullpen support and park factor because I haven’t had time to dig into the numbers yet) Carlos Carrasco and Danny Salazar combined for about 5.9 WAR, which over 161 games is a .037 hit to the Indians’ W%. Of course, the real impact is not necessarily equal to the WAR impact; generic replacements don’t apply and the impact of starting pitchers in the playoffs can be muted. Still, this adjustment is better than nothing. I should also note that not park adjusting is mildly conservative since Cleveland tends to be a pitchers park.

Knocking .037 points off of Cleveland’s three W% metrics, the resulting CTRs are:



One thing to note here is just how good Boston is assumed to be; they were excellent in the W% estimators. The Cubs were even better in each of those metrics their 103 wins would suggest, but the Red Sox close the gap on strength of schedule, 104 to the Cubs’ 93 (implying that Boston’s average opponent would have a .528 W% against Chicago’s average opponent). With the injury adjustment the Indians are the weakest team on paper, but not so much so that they have significantly lower odds (last year, the Mets at 104 were the lowest-rated team and we know how that worked out).

Wildcard odds are the least useful, since it is the round where pitching matchup has the biggest effect:



Since we’re assuming the home team wins 54.2%, there’s very little difference in assumed strength in these two matchups (of course, the Mets suffer from even more extreme pitching maladies than do the Indians).

In the charts that follow, “P” is the probability that the series occurs; P(H win) is the probability that the home team wins should the series occur; and P(H) is the probability that the series occurs and that the home team wins [P*P(H win)].

LDS:



My guess, based on no calculations but including my inherent knowledge of the team’s statistical records and characteristics, was that Cleveland would have a 45% chance against Boston. So strike one for homerism there. Texas/wildcard figures will be the closest DS matchup on paper, although I’m most eager to see WAS/LA (other than the Indians, of course).

LCS:



You’ll note that the Cubs have a higher probability against stronger teams than they do in the NLDS thanks to the extra games. Cubs/Dodgers is the most lopsided potential LCS, while Dodgers/Mets is the closest.

World Series:



The AL is favored in 13 of the 25 possible matchups, but 13 of 20 that don’t involve Chicago. It doesn’t help the stronger circuit that it’s two highest seeds have the two lowest CTRs in the field.

Putting it all together:



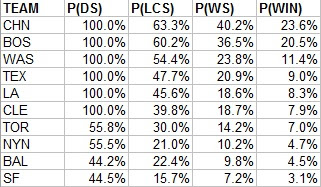
This gives the NL a 51.1% chance to win, a 84% chance of an outcome I like, a 79% chance of an outcome I really like, and a 7.9% chance of an outcome that would be the best thing that’s ever happened in baseball. Plus a 100% of being a better outcome than 2015.

Great Moments in CBSSports Box Scores

The Willie Davis Method and OPS+ Park Factors

This post is going to lay out the math necessary to apply the so-called "Willie Davis method" of Bill James to his Runs Created and to Base Runs. The last three posts have explained how you can use it with Linear Weights. This is offered in the interest of comprehensiveness, should you decide that you’d like to fiddle with this stuff yourself.

The Willie Davis method as explained by Bill James is based on the most basic RC formula, (H + W)*TB/(AB + W). You could use one of the technical RC versions too, of course, but then you would introduce the problem of what to do with all of the ancillary categories that are included in those versions. A minor modification that would help matters is to give a weight to walks in the B factor (which is simply TB in the basic version), but James has never done that as it would complicate the basic version and mess up all of the neat little RC properties like OBA*SLG*AB = runs.

While I tried to emphasize that I wouldn’t take any of the results from the linear weight translations too seriously, the output of the Willie Davis method is actually used by Sean Forman to calculate OPS+ at baseball-reference.com. So while James used it in the vein that I advocate, Forman uses it to park-adjust the most-looked at total offensive statistic at his site. For this reason, I’ll compare park-adjusted OPS+ figured by his method to what I would do later in the post.

To apply the Willie Davis method to RC, first define a = 1 + W/H, b = TB/H, and outs as AB-H. You also need to calculate New RC, which I will abbreviate as N. That is just regular RC times the adjustment factor you are using (in a park case, if the PF is 1.05 then N is RC*1.05). Then this relationship holds:

N = (a*H)*(b*H)/(a*H + Outs)

This can be manipulated into a quadratic equation:

abH^2 - NaH - N*Outs = 0

And then we can use the quadratic equation to solve for H, which we’ll call H’:

H' = (Na + sqrt((Na)^2 + 4ab(N*Outs)))/(2ab)

The adjustment factor for all of the basic components (S, D, T, HR, W with outs staying fixed) is simply H'/H. So we multiply the positive events by H'/H and the result is a translated batting line.

Since we have applied this type of approach to RC and LW, we might as well do it for Base Runs as well. Allow me to start with this particular BsR equation, published some time ago by David Smyth:

A = S + D + T + W
B = .78S + 2.34D + 3.9T + 2.34HR + .039W
C = AB - H = outs
D = HR

BsR is of course A*B/(B + C) + D, and New BsR (N) is BsR*adjustment factor. To write everything in terms of singles, let’s define a, b, and c (of course, I didn’t realize until after I wrote this that a, b, and c are terrible abbreviations in this case, but I already had them in my spreadsheet and it would have been a real pain to change everything):

a = (S + D + T + W)/S

b = (.78S + 2.34D + 3.9T + 2.34HR + .039W)/S

c = HR/S

Then we need to solve for S' (the new number of singles) in this equation:

aS'*bS'/(bS' + Outs) + cS' = N

This results in a quadratic equation just as the RC approach does, and it can be solved:

S' = (Nb - cOuts + sqrt((cOuts - Nb)^2 + 4(NOuts)(ab + bc)))/(2*(ab + bc))

S'/S is then the multiplier for all of the positive events.

So we have three different approaches based on three different run estimators to accomplish the same task. Which one should be used? Unfortunately, there’s no good empirical way to test these approaches; the entire point of having them is to make estimates of equivalent value under different conditions…i.e. conditions that did not occur in reality.

However, I think it should be self-evident that the quality of the model from which the estimate is derived says a lot about its value. I don’t need to beat that horse again, but it is well-known that Basic RC is not a very good estimator when applied to individuals, which is exactly what we are doing here.

It would also follow that the Linear Weights-based approach should be marginally better than the Base Runs-based approach since BsR should not be applied directly to individuals. Since BsR is better constructed than RC, though, the discrepancies shouldn’t be as bothersome.

I am going to use the three approaches to derive park-adjusted BA, OBA, and SLG for the 1995 Rockies. In all of the calculations, I am using a 1.23 park factor for Coors Field. The unshaded columns are the players’ raw, unadjusted numbers; the pink columns are adjusted by the RC approach, orange by the ERP approach, and yellow by the BsR approach:



From eyeballing the numbers, I’d say that there is a strong degree of agreement between the ERP and BsR estimates, with the RC estimates as the outliers. As mentioned above, this is along the lines of what I would have expected to see, as both ERP and BsR are better models of the run scoring process than RC. That the ERP and BsR results are close should not come as a surprise, as both estimators give similar weight to each event.

Using RC results in a less severe park adjustment for most players. Why is this? My guess is that it is because RC, with it’s well-known flaw of overvaluing high-end performance, naturally needs to draw down the player’s OBA and SLG less then ERP or BsR to still maintain a high performance. In other words, RC overestimates Larry Walker’s run contribution to begin with, and since the problem only gets worse as OBA and SLG increase, it doesn’t take that that big of a change in OBA or SLG to reduce run value by X%.

As I mentioned earlier, I think it is worth looking at the Willie Davis method closely since some sources (particularly Baseball-Reference) use it for serious things like park-adjusting OPS+. This is in contrast to the position of its creator, Bill James, who presented it more as a toy that yields a rough estimate of what an equal value performance would look like in a different environment.

So, here are the OPS+ figures for the 1995 Rockies figured seven different ways. Let me note off the bat that I am using OBA = (H + W)/(AB + W); for this reason and the fact that I am using my own Coors PF, we should not anticipate exact agreement between these OPS+ results and the ones on Baseball-Reference. The league OBA in the 1995 NL was .328, and SLG was .408, so the basic formula for OPS+ is:

OPS+ = 100*(OBA/.328 + SLG/.408 - 1)

The first column of the table, "unadj" uses the player’s raw stats with no park adjustment. The second column, "trad", reflects the traditional method of figuring OPS+ used by Pete Palmer in The Hidden Game of Baseball, Total Baseball, and the ESPN Baseball Encyclopedia: simply divide OPS+ by the runs park factor (1.23) in this case.

The third column, "sqrt", adjusts OBA and SLG separately by dividing each by the square root of park factor, and uses these adjusted figures in the OPS+ formula above (*). The fourth column, "reg", uses the runs factor to estimate an OPS+ park factor based on a regression equation that relates OPS+ to adjusted runs/out (this is covered in the digression as well).

Finally there are three shaded columns, which use the translated OBA and SLG results from RC, ERP, and BsR respectively as the inputs into the OPS+ equations:



What can we see from this? The traditional approach is more severe than any of the Willie Davis approaches, while the square root approach is a pretty good match for the Willie Davis approaches. Thus, I suggest that the best combination of ease and accuracy in calculating OPS+ is to divide OBA and SLG by the square root of park factor, then plug the adjusted OBA and SLG into the OPS+ equation.

Of course, I should point out that 1995 Coors Field and its 1.23 park factor is one of the most extreme cases in the history of the game. For run of the mill environments, we should expect to see little difference regardless of how the park adjustments are applied, and so I am NOT saying that you should disregard the OPS+ figures on Baseball-Reference (although I do wish that OPS+ would be pushed aside in favor of better comprehensive rate stats). On the other hand, though, I see no reason to use a complicated park adjustment method like the Wille Davis approach when there are much easier approaches which we have some reason to believe better reflect true value.

(*) I shunted some topics down here into a digression because it covers a lot of ground that I’ve covered before and is even drier than what is above. And a lot of sabermetricians are sick and tired of talking about OPS, and I don’t blame them, so just skip this part if you don’t want to rehash it.

As I’ve explained before, OPS+ can be thought of as a quick approximation of runs/out. Some novice sabermetricians are surprised when they discover that OPS+ is adjusted OBA plus adjusted SLG minus one rather than OPS divided by league OPS. And it’s true that the name OPS+ can be misleading, but it is also true that it is a much better metric. One reason is that OPS/LgOPS does not have a 1:1 relationship with runs/out; it has a 2:1 relationship. If a team is 5% above the league average in OPS, your best guess is that they will score 10% more runs. So the OPS/LgOPS ratio has no inherent meaning; to convert it to an estimated unit, you would have to multiply by two and subtract one.

The other reason why OPS+ is superior is that it gives a higher weight to OBA. It doesn’t go far enough--the OBA weight should be something like 1.7 (assuming SLG is weighted at 1), while OPS+ only brings it up to around 1.2--insufficient, but still better than nothing.

Anyway, if you run a regression to estimate adjusted runs/out from OPS+, you find that it’s pretty close to a 1:1 relationship, particularly if you include HB in your OBA. I haven’t though, and so the relationship is something like 1.06(OPS+) - .06 = adjusted runs/out (again, it should be very close to 1:1 if you calculate OPS+ like a non-lazy person). The "reg" park adjustment, then, is to substitute the park factor for adjusted runs/out and solve for OPS+, giving an OPS+ park factor:

OPS+ park factor = (runs park factor + .06)/1.06

The slope of the line relating OPS+ to runs/out is not particularly steep, and so this is an almost negligible adjustment--for Coors Field and its 1.23 run park factor, we get a 1.217 OPS+ park factor.

Now a word about the traditional runs factor v. the individual square root adjustments. Since OPS+ is being used as a stand-in for run creation relative to the league average, I would assume that the goal in choosing a park adjustment approach is to provide the best match between adjusted OPS+ and adjusted runs/out. It turns out that if you figure relative ERP/Out for the ’95 Rockies players, the results are fairly consistent with the ERP/BsR translated OPS+. Thus, I am going to assume that those are the “best” adjusted OPS+ results, and that any simple park adjustment approach should hope to approximate them.

As a consequence, the square root adjustments to OBA and SLG look the best. Why is this? I’m not exactly sure; one might think that since OPS+ is a stand-in for relative runs/out, we should expect that the best adjustment approach once we already have unadjusted OPS+ is to divide by park factor. Yet we can get better results by adjusting each component individually by the square root of PF. OPS+ is far from a perfect approximation of relative runs/out, though, so it may not be that surprising that applying OPS+ logic to park factors is not quite optimal either.

Interestingly, the justification for the square root adjustment can be seen by looking at Runs Created in its OBA*SLG form. While OBA*SLG gives you an estimate of runs/at bat, not runs/out, it is of course related. If you take OBA/sqrt(PF)*SLG/sqrt(PF) you get OBA*SLG/(sqrt(PF)*sqrt(PF)) = OBA*SLG/PF

It is quite possible that there is a different power you could raise PF to that would provide a better match for our ERP-based OPS+ estimates, but getting any more in-depth would defeat the purpose of having a crude tool. In fact, I think that adjusting OPS+ by the Willie Davis method goes too far as well. Regardless, I would be remiss if I didn’t again emphasize that the 1995 Rockies are an extreme case, and so while the differences between the approaches may appear to be significant, they really aren’t 99% of the time.