Providing Zero Insight, but Filling Space Nonetheless

In Bill James’ early Abstracts, he had a little box entitled “Talent Analysis” for each team that estimated the composite value of all of its players (as estimated by the Approximate Value method), what percentage of it was acquired through various means (trades, free agency, development), what percentage of it fell into defined age categories (“young”, “prime”, “past-prime”, and “old”), and how much total value had been produced by the team’s farm system. This article is going to be in the spirit of those and look solely at the offensive players for 2007, and without regard to ho w players were acquired, only whether they were products of the farm system or not. Also, I have omitted the age breakdowns, although I may look at that in the future.

I should note that I do not consider my examination here to be particularly insightful, and certainly it is not unique. This is the kind of stuff that I sometimes figure myself and keep to myself, but since I still can’t (or, more accurately, want to go through the effort to do so) access my pre-written articles, I have to fill this space up with something.

I also would be remiss if I did not point out that this strain of analysis did not die with the Abstract, but is in fact being practiced in other places, most notably by Steve Treder at the Hardball Times. So not only am I just ripping off James’ idea, I’m covering old ground.

Now, for a long list of caveats. One is that I have only considered hitters, and furthermore only hitters with 300 PA. So there are guys who were injured or who were part-time players or what have you and really did have value that are being ignored here.

Second is that I have used my own personal WAR figures, except I have multiplied them all by seven, and put a floor of zero on them. I did this because I didn’t want to get caught up in the numbers as WAR, but wanted something with a direct linear relationship to WAR. The result is a number that looks kind of like a fantasy dollar value--it's not, don’t go out and bid $65 for ARod in your fantasy league because he gets 65 points here, but the scale at least resembles fantasy dollar values.

If you read all of my stuff, you might be thinking “That’s awfully hypocritical, considering he doesn’t like unitless numbers like OPS or EQA”. Duly noted. However, the distinction as I see it is that WAR*7 has a direct, one-step relationship to a meaningful unit (just as Win Shares does, in theory). OPS needs an addition and a multiplication to be a decent run estimator, while EQA differences and ratios are unitless.

Third, I did not factor in defensive value, so everyone is assumed to be an average fielder at his position, thus making Hanley Ramirez the most valuable player in the NL, which I obviously don’t agree with.

Fourth, the system for classifying the producing organization of each player is not optimal. I credited each player to the franchise for which he made his major league debut. Obviously, players often change hands in the minors, and thus you might want to credit Grady Sizemore to the Nationals rather than the Indians. First major league organization is easy to do, though, and I don’t think it’s too much worse than going by signing organization. I believe that in Treder’s analysis, he tries to identify the organization most responsible for the player’s development, which could be either. This is a better approach, but I kept it simple here.

Fifth, the method of assigning players to teams was the same I used in my end of season stat reports, which means each player is credited to just one team even if played a significant amount with two teams (i.e. Saltalamacchia, whose name I find easier to spell than the star first baseman he was traded for).

Finally, I already slipped this in, but I only considered offensive players. So pitching, both on the team and produced by the system, has been completely ignored.

There are a number of different ways to look at the data, and what I am going to do is discuss a few of the interesting things, and then post a big chart at the bottom with all of the data.

Looking at the total (TOT) is not very interesting, because on the team level this just points out teams with talented position players. More interesting is the HG column, which measures homegrown talent retained by the team this year (actually, it includes anyone who made their major league debut with the team and played for So Sammy Sosa is considered homegrown for the Rangers despite the fact that he had been gone from the organization for more than fifteen years).

The leader in homegrown value was the Marlins, with 193 points. The next four teams on the list (Brewers, Phillies, Rockies, Braves) are all Neanderthal League outfits as well, while the Yankees top the AL, with a wide gap from those six teams back to the Indians.

The fact that the Yankees have a lot of homegrown value (James called it talent, and I may slip up and use that term too, but I want to stress that this is a measure of 2007 value and not talent) at first seems surprising, but consider Jorge Posada, Derek Jeter, and Robinson Cano all contributed significant value. Their total is boosted by the presence of Hideki Matsui, who in reality is a free agent signing, but here is treated as a Yankee product since he debuted in the majors with them.

There are a lot of good teams at the top of the homegrown list, but there are some pretty solid teams near the bottom too. One of those is the Cubs, with just 13 points of homegrown value (all contributed by Ryan Theriot). They are beat out by the Giants, though, whose seven points were all contributed by Pedro Feliz.

A logical jump is HG%, which is the percentage of total value produced by the team’s system. As you would expect, this has a strong correlation with the raw HG figure. Milwaukee led the way with 94% homegrown, with Florida, Minnesota, Colorado, and Philadelphia rounding out the top five. The Brewers got just 12 points from imported players (Johnny Estrada and Kevin Mench).

On the flip side, the Cubs (9%) and the Giants (7%) are the trailers. Teams as a whole got 55% of their offensive production from players they had developed.

Moving on, we have the “PROD” column, which measures the amount of value produced by the system. The leaders are the Indians with 278, just edging out the Marlins’ 273. I’ll look at the Tribe more closely in a bit, but Florida has produced 6 20 point players (~3 WAR), of which they retain(ed) five (Miguel Cabrera is now a goner). Only Edgar Renteria is gone. This may seem surprising considering the fire sales they have held, but a lot of the players they gave up in those trades were imports to begin with (Sheffield, Alou, Lowell), or no longer are around to produce any value.

The mean production is 161, pegging the Astros (162) and the Mets (158) as the most average organizations. The standard deviation is 66. I say this to set up that the z-scores range from -1.77 (Cubs) to +1.77 (Indians). With one exception, another half a standard deviation (-2.26) away from any other team. That team is the Giants.

When you see that the Cubs have only produced 44 points (around 6 WAR) of value, you can see that this is pretty bad. Their most notable contribution came from Brendan Harris (22), with the aforementioned Theriot next and just Corey Patterson and Ross Gload to chip in. But the Giants are on a whole different plane with a pitifutl 12. Only two San Fran products batted 300 teams with positive WAR this season--Feliz (7 points) and Yorvit Torrealba (5). I realize that this analysis overlooks a lot, especially pitchers, of which the Giants have a promising crop and a few good exiles out there. But it still strikes me as absurd that they rewarded Brian Sabean with a contract extension. Sabean got just two mediocre (for a playoff team) playoff teams out of four seasons of the greatest offensive force in baseball history, and his team has not been a real factor for a few years now. He has built an impossibly old team (although in his defense he has traded no prospects of offensive value to get it). You’re going to tell him “Nice job, we’d like another five years of this?”

Moving on, I have a column “%Retain”, which is the percentage of value produced by the system retained by the system (HG/PROD). The Rockies lead the way at 91%--only the Juans, Pierre and Uribe, are no longer members of the organization. They are followed by Philadelphia, Cincinnati, Detroit, and Milwaukee. The Tigers’ system has not produced much (61), but they retain 47 of it, and I doubt they’re too broken up about not having Juan Encarnacion, Frank Catalanotto, and Nook Logan. The major league average is 55%, which if you think about it makes sense--it has to be the same as the HG% on the league level.

On the other side of things, the White Sox stick out like a sore thumb with just 12% retention (the Padres are next at 26%). Magglio Ordonez, Carlos Lee, Aaron Rowand, Mike Cameron, and Frank Thomas are all 20 point players who have taken their services elsewhere by whatever means, while their most valuable retained product is a Japanese exception, Tadahito Iguchi. Josh Fields (10) is the most valuable true White Sock standing.

The “#” column gives the total number of players in the sample produced by each team, and “per #” is the per player average value produced by a system. The top three in producing players are Atlanta with 14, then Cleveland and Florida with 13. The average is eight and a third. The bottom three are San Francisco with 2, the Cubs with 3, and Detroit and Baltimore with five. Of course these lists are similar to the value produced lists.

In terms of value per farm product, Florida leads the way at 30, followed by the Yankees (27), Seattle, Philadelphia, and Colorado (26). Detroit has just 12 per player, Chicago 11, and San Francisco 6. So again, not only are the Cubs and Giants last in total value and players produced, the players that they have come up with are the least valuable.

You can play around with a lot of different combinations of the columns, but the last I will present is “Surplus”, which is the raw difference between Total and Production. A positive surplus means that the team had more value in 2007 than its system had produced. The average of course is zero, with the Astros (-4) being the closest. They, most notably, have lost Bobby Abreu, Luis Gonzalez, and Kenny Lofton, but they have also brought in Carlos Lee, Mark Loretta, and Mike Lamb with offsetting value (at least for 2007--the three that got away would have been a much bigger drain in, say, 2001).

The team with the biggest surplus (149) is Detroit, which has imported all of its notable offensive players except Curtis Granderson (Ordonez, Guillen, Polanco, Sheffield, Rodriguez). The flip side of the coin is their divisional foes, Cleveland. The Indians are short 124 points of value. You could make a pretty good team out of Indian exports (C: Josh Bard 1B: Sean Casey 2B: Brandon Phillips 3B: Kevin Kouzmanoff LF: Manny Ramirez CF: Coco Crisp RF: Brian Giles DH: Jim Thome). Even without a shortstop (and John McDonald is probably at least close to replacement level when you consider his defense), this team would have 157 points, which would rank it eighth in baseball (just ahead of the real Indians at 154).

Which feat do you find more impressive? That the Tigers have built a playoff contender on the basis of players brought in from elsewhere, or that the Indians have built a playoff team despite losing all of those players. It helps, I guess, that both teams have significant home grown pitching (on one hand Verlander, Zumaya, Bonderman, Robertson; on the other, Sabathia, Carmona, Betancourt).

Here’s a frivolous question for you: which team possessed the most value produced by another team? My off the cuff guess is the Yankees from the Mariners, on the strength of Alex Rodriguez. And that is indeed the answer. However, the second place finish is based on three players instead of just one--the Padres have 58 points of value produced by the Indians in Josh Bard, Kevin Kouzmanoff, and Brian Giles.

Here is the complete chart, which I sorted by total value produced:

Hitting by Position, 2007

This is a good once a year, mail-it-in type of post. As always, remember that we are dealing with just one year of data here, so it is not particularly significant, and any surprising findings should be viewed in that light. Nonetheless, it is a topic that I am always interested in and have fun looking at.

The data came from the Baseball Direct Scoreboard, which gets its data from STATS. I entered into the spreadsheet by hand, so I may have made a few errors, and those are my fault, not those of the Baseball Direct Scoreboard (I initially had Marlins shortstops down for 500+ walks, rather than the correct 53, and didn’t catch this until I looked at the position totals and shortstops came out as above average).

The first chart I have for you is the composite hitting by position. In addition to the standard positions, I like to look at 1B and DH together, and corner outfielders together. The “MLB” row are the MLB totals; they are not the same as the result you would get for all of the positions because of the way STATS compiles the data (pinch hitters don’t count, and there might be some other stuff). The “POS” row is the composite of the non-pitcher positions. “RC” is the basic version of ERP, as I did not include SB or CS data, and “PADJ” is the one-year offensive positional adjustment for each position, figured by dividing the position’s RG by the average position RG. “HPADJ” is the ten-year PADJ from 1992-2001 as a sort of baseline to compare against:

Again, I don’t want to read too much into the one-year data, but you can see that the range between positions is smaller than in the 1992-2001 period.

Insert obligatory comments on pitcher hitting and inflammatory comments about the Neanderthal League here. Pitchers created runs at a whopping 8% clip compared to position players. The top group of pitchers in terms of RAA compared to an average pitcher was the Cardinals, who took this coveted title for the second year in a row with a .195/.223/.238 line, +8 runs, three runs better than the Diamondbacks, Mets, and Dodgers. The worst was the Nationals at .112/.135/.138, -7 runs, just edging out the -6 turned in by the Astros, Giants, and Reds. Toronto pitchers had fun during interleague play, turning in 8 singles and a double in 22 PA for an above-total MLB average 5.1 RG.

I thought it would be fun to run a chart this year of the worst hitting teams at each position, which I have not done before. The best hitting teams at each position is boring, because the best players play almost all the time, and they usually play the same position. So it’s not at all interesting to report that the best hitting third base outfit was in the Bronx. However, the trailer list is a little more interesting, since bad players don’t usually take all 600 PAs themselves. So here are the worst at each position (no park or league adjustments here, BTW). The “RAA” column is against the average RG for the position in 2007:

Teams managed to overcome one bad position, as Cleveland and Arizona made the playoffs (although Arizona’s overall offense was poor; Cleveland was a bit above average). However, I can’t recommend being like the White Sox and having black holes at two positions.

A junk final thing I like to look at is the correlation, on a team level, between the long-term PADJ and the positional RGs. A positive correlation indicates that the team got their biggest offensive contributions from the left end of the defensive spectrum positions that you would expect; negative correlations indicate the opposite. Here are the team correlations (pitchers are not included for anyone and DH not for the NL). “AVG” is the average of the team figures, while “MLB” is the correlation between PADJ and RG for each position in the majors, individually:

I will show the data for three teams: the Astros, who had the strongest positive correlation; the Orioles, who had the weakest correlation; and the Yankees, who had the strongest negative correlation. The chart shows the position’s RG, the position’s ARG against the overall team RG (for the positions considered, i.e. no pitchers or NL DHs), and the 1992-2001 PADJ for each position as a benchmark:

The Astros repeat this honor; they led last year at +.91. You can see that they are weak up the middle, but get production out of the corners. Their team offensive spectrum goes 1B, LF, CF, RF, 3B, 2B, C, SS. Only CF is really misplaced relative to the defensive spectrum.

The Orioles’ correlation of +.03 is the lowest absolute correlation of any team, and you can see that by glancing at the numbers--they are over the map. The middle infielders are much better than the norm and their left fielders were the worst in baseball, but most of the other positions are fairly close to where one would expect.

The Yankees represent another repeat leader, as the correlation was the same -.34 in 2006. Six of their nine positions went the opposite way of what you would expect (i.e. you would expect first baseman to be above average; theirs were below average).

To end frivolously, I was impressed with the similarity between the production of the Cardinals’ center and right fielders. There may be better matches out there, but this one just happened to catch my eye. CF had 637 AB, RF 638. They each rapped out 170 hits, but RF had a little more power, winning in doubles (34-30) and homers (20-19). Triples went to center fielders 3-2, and the walk column was in their favor 56-49. Adding it all up, CF made 464 outs, RF 465. The center fielders created 87 runs and right fielders 86, giving them a 4.71 to 4.66 RG edge.

Raw data (stats by position for each team)

The Classes of 2003 and 2008

I felt that it was a very nice little coincidence this week when the two blockbuster trades both involved a young outfielder who first made a name for himself as a big high school prospect in the 2003 amateur draft. It is especially noteworthy to me, as I myself am a member of the class of 2003. Now of course I am not and never have been a major league prospect, but it is not hard to feel a bit of a connection to the players in the exact same age range as you, who are reaching adulthood at the same time as you. In basketball we had LeBron James to bear our standard, and in baseball, Delmon Young and Lastings Milledge were two of our very best prospects.

On the trades themselves, my opinion is not particularly interesting, since I have no special insight on the players and so many other voices have already weighed in. I think that the Rays-Twins trade was just a great baseball trade, one that will be fun to watch over the years to see who emerges on top. Were I running things in Tampa Bay, I would have found it very difficult to trade away a talent like Delmon Young, and I’m not usually one impressed by toolsy players with pitiful walk rates. If I had to guess, I’d say Matt Garza is able to provide more early value, but eventually the Twins win the deal. It’s a great trade, though, because eminently reasonable people can view it any number of ways.

The same will not be said of the Milledge deal. There is very little that can be said in defense of it, it seems; most comments that are not made by people with jaws on the floor tend to stress that Milledge is not that good of a prospect, and that the trade is not an all-time debacle. If that is the best that can be said for a deal, then it almost certainly shouldn’t have been made.

I have also seen the point raised that critics of the trade are overstating not only Milledge’s prospects but his trade value, and that Minaya obviously found that the value was only Schneider and Church. I have two problems with this argument, the first of which is simply that because Minaya felt that Schneider and Church was the most valuable package he could receive does not make it so.

The second is that the argument treats the relationship between a ballplayer and his general manager in the same manner as the relationship between a gallon of milk and a store manager. Even if we suppose that the Nationals’ package represents the extent of Milledge’s value, he’s not a commodity with an expiration date. He doesn’t need to be cashed in.

If I may make an even more ridiculous analogy, the relationship between the GM and the player is more like the relationship between me and my car. I have a car, and it has a certain resale value; which, in the case of my lovely early 1990s automobile, not a whole heckuva lot, but someone would take it at some price. If I sold the car, the best I might be able to get for it is $1,000. So if I do sell it for $1,000, have I made a good deal? After all, I got fair market value for it.

My answer is: depends. I was under no obligation to sell the car, so we have to consider other factors, like how much it will cost to replace my car. A better example is probably the stock market. If I sell a stock for $15, I have by definition received fair market value--there's not even a question about it. But if you were an investment advisor, would you just tell your clients to feel free to buy and sell stocks willy-nilly, just because by definition any stock transaction is a fair deal?

My point is that just because Milledge has X trade value doesn’t justify a decision to trade him for X. This is a trade for which it is very hard to see the upside for the Mets. If Brian Schneider and Ryan Church are going to outperform whoever the Mets’ other alternatives for their roster spots would have been, and doing so will make a significant impact on their fortunes, than I would submit that it is going to be a rough year in Queens.

Moving on, there is the Class of 2008. The potential Hall of Fame class, that is. As I have written before, I don’t really care about who goes into the HOF, because I don’t believe that the HOF has any capacity to honor the truly great players anymore (and “anymore” is not a new condition; the situation dates back to the 1970s at least) . I care a little bit, to about the same extent as I care about who wins NBA games. If Bert Blyleven is finally elected, it will still not be an honor to tell him that he is in the same class as Rube Marquard. As far as I am concerned, they can only dishonor him by waiting a dozen years before considering him worthy of standing aside Marquard.

If it was just Marquard, that would be on thing. But it’s not--it's Pop Haines, and Catfish Hunter, and Bob Lemon, and Chief Bender, and Dizzy Dean, and Jack Chesbro, and Lefty Gomez. None of whom should flatter Blyleven, or Tommy John for that matter, as company.

So I try to stay out of the HOF debates; while I like the “who was better than who” exercise as much as any baseball fan, it’s a lot more interesting to make your own lists, or follow along with something like the Hall of Merit or to just argue about players on a message board. So I’m not going to write an essay begging and pleading for the induction of Alan Trammell, Bert Blyleven, Tommy John, Goose Gossage, Mark McGwire, and Tim Raines, or bemoaning the fact that the BBWAA voters didn’t even give Lou Whitaker a second chance on the ballot. I’m going to write a sentence that does that, and move on with my life. Now excuse me; the Bobcats might be playing the Clippers right now.

Tangent Lines and Bill Kross

This is a math post with little baseball content and no baseball insight, so be forewarned.

In calculus, at least as far as I understand it, the tangent line is a line that intersects a point on a curve in the same direction as the curve, and the line has the same slope as exists on the curve at the point. That’s the best I can do--see this Wikipedia article for a better description.

Anyway, the tangent line is linear (it can be written as y = mx + b), and it shares the same slope as the line that it intersects. That means that near the point in question, it is just about the best linear approximation that you can get.

Where this ties into baseball is that if we have a non-linear function and want a linear approximation to it, the tangent line can be a shortcut that is easier and quicker than generating a line through some other technique (such as regression). Understanding how the tangent line works can also help us understand why non-linear baseball models have the linear approximations that they do.

First, let’s calculate a tangent line for a non-baseball problem. Suppose we have the line z = x^3, and we want a tangent line at the point x = 3. At x = 3, z = 3^3 = 27. The slope at x =3 can be found by first taking the derivative of z, which is z’ = 3x^2, so z’(3) = 3(3)^2 = 27.

We can write the line in the point-slope format as y - y1 = m(x - x1), where y1 and x1 are the base (x,y) point and m is the slope. So y - 27 = 27(x - 3). We can convert this to the common y = mx + b form to get y = 27x - 54.

At x =3, y = 27(3) - 54 = 27, which is exactly equal to z, as we know it should be. If we look at another x value close to 3, say 3.1, we get z = 29.791. We get y = 29.7. As you can see, they are pretty close. As we get further away, the linear approximation will perform worse, especially for functions with a steep slope.

Now, let’s talk about some of the baseball relationships where this is applicable. Clay Davenport used to publish a team version of EQR in which (RAW/LgRAW)^2 approximated the percentage to which the team R/PA exceeded the league average. There is also a linear version (which is the only one I have seen Clay publish in some time), in which the mapping is 2*(RAW/LgRAW) - 1.

Let’s call RAW/LgRAW “ARAW” for adjusted RAW. The two relationships we have are ARAW^2 and 2*ARAW - 1. Now suppose we work with the exponential function and find the tangent line at the league average point, where ARAW = 1 and the result of the formula = 1 (this is common sense, as a team with a RAW equal to the league average should score runs at a rate equal to the league average). The slope of ARAW^2 is 2*ARAW, which is 2*1 = 2 when ARAW = 1. So y - 1 = 2*(ARAW - 1), and y = 2*ARAW - 1. As you can see, that is the other Davenport
formula.

This is no surprise, as even if Davenport derived the relationship through a regression approach, we would expect the best fit to be about the same as the point at the league average, since most of the teams are tightly clustered around that point.

Another stat which follows the same relationship to runs is OPS. David Smyth (and perhaps others, but I recall seeing David write it) has pointed out that the square of relative OPS (not OPS+, but straight OPS/LgOPS) tracks runs, and Steve Mann wrote about the similar 2*(OPS/LgOPS) - 1 relationship eighteen years ago in The Baseball Superstats 1989.

The most interesting relationship, though, is the Pythagorean win estimator. I have written about this before on my website. Pyth can be written as:

WR = RR^z

Where WR is the win ratio (W/L), RR is the run ratio (R/RA), and z is the exponent (usually seen as z = 2). We know that for an average team, RR = WR = 1. The slope of the function is z*RR^(z - 1). If z =2, then it is just 2*RR, which is 2 when RR = 1. If z = 1.83 (another common value), than it would be 1.83*RR^.83, which is 1.83*RR when RR = 1.

We know that W% = WR/(WR + 1). We can therefore write this as a W% estimator as W% = (2*RR - 1)/(2*RR).

This method of estimating W% was discussed, informally, by Bill James in the 1984 Baseball Abstract. James said that if a team scored 10% more runs than their opponents, they should win 20% more games. He wrote that he had never tried it but it “should work”, and dubbed it “Double the Edge”. I have no idea whether Bill came up with this through similar mathematical logic to what you see here, or whether it was intuitive. With James, I’d believe either.

Anyway, the good thing about this estimator is that it caps W% at 1. However, it does not bottom out at zero--a RR of less than .5 results in a negative W%.

Ralph Caola, who has done a lot of work on run to win converters, emailed me after reading the article on my site and suggested that to solve this problem, one could use two equations: one when Run Ratio is greater than one, and one when Run Ratio is less than one. For the less than case, you could define W% as 1 - (2*OppRR - 1)/(2*OppRR), where OppRR is the opponents’ run ratio, RA/R. This way, reciprocal run ratios would produce complementary W%s, as we would intuitively expect (and as Pythagorean gives).

This way, reciprocal run ratios would produce complementary W%s, as we would intuitively expect (and as Pythagorean gives).

There are dozens of ways you can write those formulas, and Ralph settled on W% = (R-RA)/(R + RA + ABS(R-RA)) + .5.

And sure enough, the equation is more accurate and more theoretically sound if you use Caola’s insight. However, I have recently realized that Ralph was not the first one to uncover this formula. In fact, it has been in the public eye for over twenty years and little has been said about it. (I am not necessarily bemoaning this, because the only reason to use the linear approximations to Pythagorean is simplicity. They are not preferable. However, with the increased presence of sabermetric research all over the place, I am a bit surprised that Ralph and I seem to have been the only ones to play around with James’ Double the Edge).

In The Hidden Game of Baseball, there is a brief description of several run to win methods in Chapter 4. In a footnote, Palmer/Thorn write “About a year after Pete’s article [in SABR’s The National Pastime] appeared, Bill Kross, a Purdue professor, devised an elegant little formula that was not only simpler than the others, but also very nearly as accurate, erring only when run differentials were extreme (+/- 200 runs). If a team is outscored by its opponents, Kross predicts its winning percentage by dividing runs scored by two time runs allowed; if a team outscores its opponents, the formula becomes, 1 - RA/(2*R).”

Remember what I said about there being dozens of different ways to write the DTE formula? I am not going to go through the algebra here, but suffice it to say that the Kross formulas are one of the dozens. I don’t know if Mr. Kross developed those by linearizing the Pythagorean formula, or through some other technique, but there it is. These formulas are not a breakthrough in accuracy, be it empirical or theoretical, but they are quick and easy and do have a strong logical foundation, and can even be seen as offshoots of Pythagorean estimators.

Leadoff Hitters, 2007

For the last two years I have written a piece giving the leading and trailing teams in various categories that can be used to evaluate leadoff performance. I always try to stress that, as numerous studies have shown, batting order construction is not as crucial as conventional wisdom holds it to be. I am personally much more concerned about how a player performs in an average situation than in any particular lineup slot.

Nonetheless, the matter of who will leadoff for a team is certainly one that is oft-discussed and is given particular attention by the men who run major league teams. Thus, it is useful to actually know which teams got good production out of the leadoff spot and which did not.

Before I start going into the various categories, let me first emphasize that the data is for team’s aggregate leadoff performance. In parentheses after each team on a list, I will give the names of the individuals who appeared in at least 20 games in the leadoff spot, but unless the player took every plate appearance of the team’s season in the #1 slot, the statistics are not solely his. Also, the 20 games does not mean 20 starts at leadoff hitter--it is 20 appearances, regardless of whether some of those came as a pinch hitter, pinch runner, defensive replacement, or what have you.

With the disclaimers out of the way, the most basic job of a leadoff hitter is to score runs. So runs scored per 25.5 outs (outs here are AB-H+CS) seem to be a good place to start:
1. PHI (Rollins), 7.2
2. MIL (Weeks/Hart), 7.2
3. DET (Granderson), 6.8
Leadoff Average, 5.6
ML Average, 4.8
28. CHA (Owens/Erstad/Podsednik), 4.5
29. STL (Eckstein/Taguchi/Miles), 4.5
30. WAS (Lopez/Logan), 4.1

Leadoff Average is the average for the team’s leadoff performances, while ML Average is the average for the league as a whole, slots one through nine. This is a sabermetric blog--I don’t need to point out to you the biases that exist in using actual runs scored data, so I will let those figures stand without comment.

Perhaps even more elemental to the traditional role of the leadoff hitter than scoring runs is getting on base. On Base Average is as important of a statistic as there is anyway, so it’s only natural to look at how the leadoff men did:
1. SEA (Suzuki), .389
2. LAA (Willits/Figgins/Matthews), .377
3. FLA (Ramirez/Amezaga), .376
Leadoff Average, .341
ML Average, .332
28. ARI (Young/Byrnes/Drew), .309
29. HOU (Biggio/Burke), .305
30. WAS (Lopez/Logan), .305

To me, the Angels high showing is a bit of a surprise, as Chone Figgins and Gary Matthews have never been huge OBA guys, and Reggie Willits was a relative unknown. On the flip side, seeing Craig Biggio and company in a virtual tie for last in baseball is somewhat sad.

A slightly modified version of OBA that is worth looking at is what I call the Runners On Base Average. ROBA removes home runs and caught stealings from the OBA numerator, leaving only those times in which a runner was actually on base to be advanced by his teammates. However, in this stat the home run is treated no differently than an out, so it is to some extent a “style” stat and not a quality stat. That is not to say that ROBA is not a practical thing to know--it is after all just the Base Runs A factor per PA. Just keep in mind that it is a statistic in which higher is usually, but not always, better:
1. SEA (Suzuki), .370
2. BAL (Roberts), .352
3. LAA (Willits/Figgins/Matthews), .351
Leadoff Average, .309
ML Average, .300
28. HOU (Biggio/Burke), .278
29. TOR (Rios/Johnson/Wells), .277
30. ARI (Young/Byrnes/Drew), .260

Not surprisingly, four of the extreme teams are holdovers from the OBA list.

Moving further down the path of style stats is Bill James’ Run Element Ratio, which divides walks and steals by extra bases. The idea behind RER was that it was the ratio of those events that are most important early in an inning (table-setting events with little advancement value like the walk) against those that are most important late in an inning, when runners are already on base (power). Singles are ignored because they serve both purposes well.

RER is not really a statement of quality at all, but a statement of shape. In theory, players with high RERs would seem to be better suited as leadoff hitters than those with low RERs, but it doesn’t necessarily mean that they are actually more productive in the role. I believe RER is most useful when discussing leadoff hitters as a tool to pick out players who don’t fit the conventional wisdom of what a leadoff hitter should be, but who were utilized as such:
1. MIN (Castillo/Casilla/Tyner/Bartlett), 2.3
2. LAA (Willits/Figgins/Matthews), 2.2
3. CHA (Owens/Erstad/Podsednik), 2.1
Leadoff Average, 1.0
ML Average, .7
28. HOU (Biggio/Burke), .5
29. DET (Granderson), .5
30. CHN (Soriano/Theriot), .4

As you can see, we have teams show up in the leaders who have previously been among the trailers in “effectiveness” categories, leaders who were previously leaders, and all other such combinations.

Going back to context neutral effectivness metrics, another Bill James’ invention was an estimated runs scored figure, based on assumptions about how often a leadoff hitter scored from each base (James used 35% from first, 55% from second, and 80% from third). I call this Leadoff Efficiency when viewed per 25.5 outs:
1. FLA (Ramirez/Amezaga), 8.1
2. MIL (Weeks/Hart), 7.6
3. BAL (Roberts), 7.6
Leadoff Average, 6.2
ML Average, 5.8
28. WAS (Lopez/Logan), 5.1
29. HOU (Biggio/Burke), 5.1
30. STL (Eckstein/Taguchi/Miles), 4.9

Of course, we can always just look at leadoff hitters the same way we would any other player, with a standard, context neutral run estimator. Using ERP as the estimator, here is good old Runs Created per Game:
1. FLA (Ramirez/Amezaga), 7.0
2. MIL (Weeks/Hart), 6.5
3. DET (Granderson), 6.5
Leadoff Average, 5.0
ML Average, 4.9
28. WAS (Lopez/Logan), 3.8
29. STL (Eckstein/Taguchi/Miles), 3.8
30. CHA (Owens/Erstad/Podsednik), 3.6

Finally, as David Smyth suggested for the first incarnation of this piece, we can look at a modified OPS with a weight of 2 for OBA. The most accurate weight for OBA is somewhere in the neighborhood of 1.7, so using 2 is closer to optimal than using 1, but serves to give a little extra boost to OBA, which may be justified when looking at leadoff hitters. The list presented below is actually (2*OBA + SLG)*.7, as the .7 multiplier makes it approximately equal to traditional OPS on the league level. Since we are dealing with meaningless units anyway, we might as well scale them to a meaningless scale with more familiarity (OPS):
1. FLA (Ramirez/Amezaga), 889
2. CHN (Soriano/Theriot), 855
3. DET (Granderson), 851
Leadoff Average, 767
ML Average, 761
28. STL (Eckstein/Taguchi/Miles), 685
29. WAS (Lopez/Logan), 679
30. CHA (Owens/Erstad/Podsednik), 673

If you are interested in looking at this stuff on your own, I have posted a Google spreadsheet with all of the data.

A Replacement Post (brought to you by eMachines)

The next few entries at this blog will test replacement level theory, as these are replacement posts. My computer on which the regular posts were stored was done in by a power surge, which apparently is a recurring problem with eMachines systems. Anyway, the disk drive appears alright, but I don’t have access to it at the moment, so it will be some time until I can publish the posts I had already written, and since they are already written, I’m not going to go back and write them again. So the 1876-1881 NL series is on hold, as well as a few other articles.

So one replacement topic will be rate stats. I still intend to finish the rate stat series in which I discuss all of the options for expressing an individual’s run creation performance in a rate form. For now, I just want to talk about the mathematical consequences of a couple approaches, not their theoretical underpinnings.

Jin-AZ at On Baseball and the Reds has been doing a sort of “Player Valuation 101” series that I would recommend to anyone, but particularly novice sabermetricians (in the interest of full disclosure, he liberally cites some of the stuff I have written in his series). Anyway, one thing that he mentioned was the choice between runs per plate appearance and runs per out to calculate individual offensive value above baseline.

Like I said, I don’t want to get into the theoretical underpinnings here, so suffice it to say, R/PA doesn’t cut it. Absolute RC methods do not account for the “inning killer” value of the out (as Tango called it in his series on run creation); this is not a flaw in their design, since they are attempting to measure the number of runs that actually resulted from the batter’s performance. But when discussing his value to a team, the inning killer value of the out must be considered. Absolute RC does not do so, and neither does the denominator of plate appearances.

Runs per out, on the other hand, should not really be directly applied to players (it is the one true rate stat for teams), but by dividing runs by outs it does incorporate the full effect of the out.

Let’s look at some actual numbers to illustrate the point. First, let’s define our RC formula as ERP, with the out values customized for the 2007 AL. Whether these particular values are correct are immaterial for the purposes of this exercise:

Abs RC = .49S + .81D + 1.13T + 1.46 HR + .32W - .09628(AB - H)
BR = .49S + .81D + 1.13T + 1.46HR + .32W - .29083(AB - H)

Let’s use David Ortiz as our example. Big Papi had 140.595 RC and 69.195 BR under these formulas in 660 PA and 367 outs.

One approach to RAA would be to take (R/O - LgR/O)*O. The league R/O was .19455, and so Ortiz was (140.595/367 - .19455)*367 = +69.195. As you can see, this is exactly equal to his Batting Runs. So while R/O may not be the ideal rate stat, using it as the fuel for the RAA figure is equivalent to using Batting Runs.

Switching subjects, during the Breeder’s Cup on Saturday, George Washington was injured in the Classic and had to be destroyed. This lead to a few European racing folks blasting the Breeder’s Cup for being run on dirt.

One of the complaints is that the Breeder’s Cup are subtitled with some variation of “world championships”, and since dirt racing is largely an American phenomenon, this is a misrepresentation. That complaint means nothing to me; if the Euros want to get agitated about the semantics of how the event markets itself, they can knock themselves out. What was obnoxious was the complaint that the event was run on the dirt at all.

Americans have always preferred dirt racing. I prefer dirt racing--it is much more conducive to speed, and speed is exciting in thoroughbred racing. America’s major events have always been run on dirt, a tradition dating back nearly 150 years for races like the Travers or the Kentucky Derby.

If European trainers think dirt is too dangerous, or they don’t think their horses will adapt well to the surface, they are free to leave their horses at home. Of course, of the eleven BC races, four are run on the turf, so it’s hardly as if the opportunity is not there. And of course the Europeans have their own high profile meets in which horses run solely on the turf.

George Washington’s connections obviously felt that he should run in the Classic. Perhaps that was a poor decision (although more likely it was a flukish event that couldn’t have been foreseen). It’s not the other Euros’ business.

It is common to see Americans, usually but not always liberal, carp about how Americans are so provincial when it comes to sports. The fact is that people all around the world have similar mindsets. Europeans thumb their nose at dirt racing, which is king in America but also practiced to limited extents in other parts of the world, including South America, Japan, and Dubai (where the world’s richest race, the World Cup, is run on the…dirt). The IOC drops baseball because it supposedly is not played by enough countries around the world. In fact, baseball is played on a high level by just about every country in North and Central America, several in South America (Venezuela and Colombia along with a lesser presence in Brazil), three major east Asian countries (Japan, Korea, and Taiwan), and Australia. What they really mean is that baseball is not played by enough European countries. Casting baseball aside as a major sport cannot be done from a global perspective. It can only be done from a Euro-centric perspective (or Africa, or West Asia, but of course it is not people from those areas that dominate these types of governing bodies).

The fact of the matter is that each individual has their own opinion about what makes good sport (mine are that baseball is easily the best sport with football a close second. Basketball played with college rules is excellent, but the NBA and international games put me to sleep. Hockey is great if played by skilled players and awful at a non-professional or collegiate level. Horse racing on the dirt is better than horse racing on the turf, but turf racing is still interesting. Soccer is the most boring thing mankind has ever invented). From the preferences of individuals rise the preferences of nations viewed as a whole, and regions. I refuse to make apologies for my individual sports preferences, and if some European trainer doesn’t like it, he can jump in a lake. And if Europeans and Africans and Brazilians (or my fellow Americans) want to kick around a checkered ball for 90 minutes, that’s no skin off my back, nor is it an excuse for soccer fans to act morally superior because their sport is played by more people than mine.

MVP

The American League MVP race is closer than it may appear to be at first glance. Magglio Ordonez was actually a more productive hitter than Alex Rodriguez on a rate basis, although the difference (9.40 to 9.35 RG) is not meaningful. In terms of RAR, not considering position, I have ARod ahead 91 to 87. Including the fact that third base is essentially a neutral offensive position while right field is a hitter’s position, ARod moves ahead +91 to +80.

However, the gap is closed again when you consider defense. Rodriguez seems to be slightly above average at third base, while Ordonez +14 UZR per 150 games in right. The difference of ten or twelve runs makes the MVP race a dead heat. However, Rodriguez is still my choice, for any number of reasons. I don’t particularly care if a player’s team made the playoffs, but it certainly doesn’t hurt, and the Yankees made it. Past performance really doesn’t have a lot of place in a MVP discussion, but being one of the great players of your generation against a good but not great player certainly doesn’t hurt either. Offensive and defensive contributions are equally valuable, but we have a better handle on measuring offense, so it doesn’t hurt when it is offense at which you have a clear edge. Ordonez’ season is also much more of a fluke from a shape perspective, as his value is driven by a .368 BA; Rodriguez betters him .497 to .363 in SEC.

Rodriguez and Ordonez tower above the other candidates; Ordonez leads the next hitter by 7 RAR, even before accounting for his excellent defense.

The four hitters in the middle of my ballot include two guys who are there on the strength of their defensive contributions--Curtis Granderson and Grady Sizemore. Both had excellent years at the plate, with Granderson +61 RAR and Sizemore +50. Defensively, UZR pegged Granderson at +18 runs/150 and Sizemore at +26. Even if you regress the defense a bit, it’s enough to put them in the mix.

Jorge Posada had an outstanding year, 45 runs better than an average AL hitter, good for fifth in the league despite being a catcher. David Ortiz, considered to have had a down year, was actually outstanding once again. His 9.31 RG essentially makes him the equal of Ordonez and Rodriguez at the plate; the only reason he is not in the mix for the top spot is he has zero defensive value. It’s enough for another top five finish, though:

1) 3B Alex Rodriguez, NYA
2) RF Magglio Ordonez, DET
3) C Jorge Posada, NYA
4) CF Curtis Granderson, DET
5) DH David Ortiz, BOS
6) CF Grady Sizemore, CLE
7) SP C.C. Sabathia, CLE
8) SP Josh Beckett, BOS
9) RF Vladimir Guerrero, LAA
10) SP John Lackey, LAA

My nimrod fan at BTF will be happy to see that there are no first basemen on the ballot. This is not because I have an inherent bias against first baseman or because my analytical system has a bias against first baseman; it is because the first baseman in the American League are just not very good. If you look at hitting RAR without considering position, the top five players are a third baseman, a right fielder, a designated hitter, a first baseman, a right fielder, a catcher, a center fielder, a center fielder, a center fielder, and a first baseman. Can we agree that a first baseman who was not among the top ten hitters in the league in all likelihood is not an MVP candidate and focus on those two? Good. Actually, even if you don’t agree, we’d have to go all the way down to number thirty to find another first baseman. By contrast, in the NL, the number two, six, eight, thirteen, fourteen, seventeen, and twenty rankings in HRAR are held by first baseman.

Of the two first baseman in question, we can eliminate the tenth-ranked Mark Teixeira right off the bat since he spent much of the year in the NL. That leaves Carlos Pena, who ranks fifth in position adjusted RAR as well, at +64. However, his UZR is -5 runs/150 games, dropping him to +59, which is still an excellent figure, but does not crack the top ten. If my ballot kept going, he would definitely be between 11-15.

Moving on to the Neanderthals, the race is seemingly more wide open. Jimmy Rollins and Matt Holliday have been popular media names, while Hanley Ramirez is tops in position-adjusted offensive measures, and names like David Wright, Chipper Jones, and Miguel Cabrera do well on those lists as well. Jake Peavy and Brandon Webb were both outstanding starting pitchers.

Let’s start weeding it down to the serious contenders. Hanley Ramirez led the NL with +66 RAA and +85 RAR. While this incorporates the fact that he is a shortstop, this does not account for the fact that he is by all accounts a dreadful shortstop. UZR puts him at -20, Chone’s metric at -20, and the RZR-based approach of Jin-AZ at -15. He’s flat out not good. This drops him out of consideration for the top of the ballot, but he was still one of the ten most valuable players in the league.

His teammate Miguel Cabrera, +73 RAR, has much the same problem. -28 UZR, -18 according to Chone…enough to drop him out of the running entirely.

Jimmy Rollins had a fine season at +68 RAR; the metrics see him as a slightly below average shortstop, so if we are generous and leave him at +68, he’s not the MVP either. Matt Holliday’s offensive stats are obviously inflated from playing at Coors; nonetheless, he was +63 RAR and is rated very highly defensively +13 according to UZR and Chone, making him a top five candidate.

Another player whose defense propels him to the top is Rollins’ double play partner, Chase Utley. +61 RAR coupled with a fairly conservative (he was +16 in UZR, +21 by Chone) fifteen runs in the field make him Holliday’s equal. Jose Reyes was +54 at shortstop, but his +23/+13 defensive performance lifts him into Rollins territory, despite the fact that his season has been portrayed as a disappointment by many.

Surprisingly, Albert Pujols also gets a huge defensive boost. +67 RAR is impressive enough, but add in his +14/+15 fielding, and he is leading the pack so far. I am a little skeptical of that high of a defensive contribution at first base, but Jin-AZ’s RZR-based metric puts him at +30! While that seems impossible, it does lend credence to the idea that he could have saved a "mere" fifteen runs in the field.

In the end though, my choice comes down to a pair of third baseman. One a longtime star and former MVP, the other a young member of the ill-fated Mets. Compared to replacement level regardless of position, Chipper Jones was +77 while David Wright was +82. Compared to an average hitter, Chipper was +60 and Wright +61. Despite having 103 less PAs, Jones was able to keep pace with Wright by leading all NL hitters other than Barry Bonds in RG.

It really is a close race between these two; Jones got the edge in WPA, +4.23 to +4.09. I don’t give this a lot of weight, but it’s another one of those factors that certainly is not a negative. It is in the defensive metrics where things get interesting. Neither made the top three at the position in UZR, so we don’t know how they rate there. By the RZR approach, Wright was ahead 24 to 8, but by the Chone approach, it was 7 to 1 in Jones’ favor. I am very skeptical of RZR, but not enough to just discount it completely and give Jones a six run defensive edge. Also, Jones’ defensive reputation has not been great throughout his career, and that is a reason for some skepticism about his showing this season.

Since Wright is slightly ahead in the main offensive measures and isn’t clearly inferior defensively, he is my choice for top NL third baseman and the MVP. Jones would be worthy of the award as well, though. Behind them, since the next wave of candidates all rely on their defensive value to differentiate themselves, I am more comfortable with those who had the edge offensively and play left defensive spectrum positions. In the end, I voted:

1) 3B David Wright, NYN
2) 3B Chipper Jones, ATL
3) 1B Albert Pujols, STL
4) 2B Chase Utley, PHI
5) LF Matt Holliday, COL
6) SP Jake Peavy, SD
7) SS Hanley Ramirez, FLA
8) SS Jimmy Rollins, PHI
9) SS Jose Reyes, NYN
10) SP Brandon Webb, ARI

Cy Young Award

Continuing to pick the award winners and set my IBA ballot (yes, I know the deadline to vote already passed, but this is pre-written), let’s move on to the Cy Young Award. Starting in the superior league, I think there are five candidates that stand out, all starters: Josh Beckett of Boston, CC Sabathia and Fausto Carmona of Cleveland, John Lackey of Los Angeles, and Johan Santana of Minnesota. Eric Bedard was on pace to rank right up there with them, but injury held him to 182 innings and kept him out of the running.

This is one of the closest Cy Young races that I can recall in some time. I remember the 1997 NL race as being a real doozy, and last year’s NL race was well-contested as well. This one ranks up there with them. Let’s start by picking Cleveland’s top pitcher. Sabathia worked twenty six more innings than Carmona, and trailed him in RA (3.58-3.33), eRA (3.83-3.61), and Quality Start Percentage (74-81). He did enjoy a substantial advantage in FIP (3.67-4.42), although since they had the same defense behind them, this does not carry as much weight with me as it might. Overall, Carmona was +37 versus average and +67 versus replacement; Sabathia was +35 and +68.

This race is too close to call by the numbers, and so my judgment call is to go with CC. I try not to buy in to the talk about “leadership” and being a “stopper” and the like, but Sabathia is the Indians’ ace. He draws the ball for the opening playoff game, he is a veteran, he strikes more batters out. If you want to see it the other way, be my guest, but I go with Sabathia.

So how does Sabathia match up to the others? He leads Lackey and Beckett by three RAR and Sabathia by eight, although Beckett edges him by one run when compared to average. These razor-thin differences are essentially meaningless, and so it again comes down to a judgment call. Beckett led in RA by .3, but Sabathia tossed 41 more innings. That means that Sabathia is equivalent to Beckett plus a pitcher with 41 innings and a 5.07 RA. Considering that the league average was a 4.90 RA, this replacement is a guy you’d like to have lying around to fill in on your staff. The difference between Sabathia and Lackey is a seventeen inning pitcher with a 3.71 RA.

That approach is equivalent to RAR, but it just frames the differences in a different perspective. I think that the extra innings are valuable, and do put Sabathia ahead, however so slightly. He is my choice, but I can accept any of the top four.

In such a tight race, some people will begin to put more emphasis on factors that often can be safely ignored, like the quality of opposition faced. I am not sure that this is appropriate. Clearly, for determining who is of better ability or who is more likely to pitch better in the future, the quality of opposition is important. However, when it comes to value, I think one can make a case either way.

Comparing to a baseline pitcher, it is clearly true that the hypothetical pitcher will allow a different number of runs depending on the type of hitters he faces. However, regardless of what kind of opposition you face, a win is a win. If the Indians faced a worse average opponent than the Red Sox, this may provide us with evidence that Boston was a better team despite having an identical record. But the Indians’ 96 wins are worth every bit as much in baseball value terms as the Red Sox are, even if they were “easier” to obtain.

My point is that there are two issues in play when discussing quality of opposition. The first issue is that a baseline pitcher, be that baseline average, replacement, or anything else, would have a different expected level of performance based on opponent quality. But the second issue is that if a team is fortunate enough to face a weaker schedule, the wins are real, the playoff appearance that results is real, the revenue that comes from increased wins is real. So to me it is not entirely clear that it should be considered from a value perspective. This is another one of the potential adjustments that pop up in sabermetrics, and I think you need to define exactly what it is that you are trying to measure before deciding whether or not to adjust. To me, too many people have a visceral reaction and say “Oh, that’s not fair, and we can come up with a reasonable estimate as to its effect, so let’s do it”, without thinking about whether it really is the right choice given the goal.

So to me, and you are of course free to disagree, quality of opposition should only be considered within the context of one’s team. If a pitcher faced a lower quality of opposition than the rest of his team, then I would hold that against him. Suppose that Sabathia and Carmona are identical pitchers in terms of quality, but Sabathia faces an average .510 opponent and Carmona an average .500 opponent (this can be though of in terms of OW%; the W% figures are just easier to work with in this context). Sabathia will have less value when we figure RAA or RAR since we don’t account for opposition quality. But it wouldn’t have mattered one bit to the fate of the Tribe if they had flipped places, and Carmona wound up having less estimate value.

(In fact, Sabathia’s opponents hit a composite .263/.329/.409 versus .263/.334/.413 for Carmona. In terms of runs, those figures imply that Sabathia’s average opponent was equivalent to 4.63 runs per game, while Carmona’s was 4.76.)

However, if Sabathia and Beckett were of identical quality, and Sabathia faced .500 opponents while Beckett faced .510, the Indians will win real games as a result of this. Whether this is fair or not is not really my concern; it is real.

I see this great race as:

1) C.C. Sabathia, CLE
2) Josh Beckett, BOS
3) John Lackey, LAA
4) Fausto Carmona, CLE
5) Johan Santana, MIN

In the Neanderthal League, things are a lot clearer. Two candidates stand out above the pack, one of whom was my choice a year ago. He is Brandon Webb, and his rival is Jake Peavy. Behind them, the second tier of candidates includes Tim Hudson, Roy Oswalt, Brad Penny, and John Smoltz.

Comparing Webb and Peavy, Webb pitched 13 more innings, but his RA was .36 higher. They were essentially even in both eRA and FIP (+.04 advantage in eRA for Peavy, +.03 for Webb in FIP). The gap between Webb and Peavy was a 13 inning pitcher allowing a 9.48 RA. Peavy leads +44 to +37 in RAA and +73 to +68 in RAR. He also pitched a quality start 82 percent of the time versus just 65 for Webb. I see no reason at all to not side with Peavy.

The other candidates have very little to separate them; I take Oswalt and Hudson over Penny because I would sleep better at night with them in my rotation. Is that stupid, arbitrary reasoning? Heck yeah. But Penny’s maximum 2 RAA and 1 RAR edge over the lesser of those two isn’t worth much either:

1) Jake Peavy, SD
2) Brandon Webb, ARI
3) Tim Hudson, ATL
4) Roy Oswalt, HOU
5) Brad Penny, LA

Rookie of the Year

The regular season is over, and thus it’s time for the annual hot stove favorite question, “Who should win the awards?” I am not immune to such general baseball fan amusement, and so I will begin here with the Rookie of the Year awards. I will also be contributing these ballots to the Internet Baseball Awards, which are now hosted by Baseball Prospectus.

As always, we begin in the modern league with modern rules that got shortchanged in the 1998 expansion. Like last year, the majority of the top AL rookie candidates are starting pitchers. Unlike last year, there were not three rookies who turned in star caliber performances; this year’s group is solid but unflashy with the exception of the big name, Daisuke Matsuzaka (+15 RAA, +43 RAR in 204 innings). The other two are Jeremy Guthrie (+17, +41, in 175) and Brian Bannister (+14, +36 in 165).

Sorting out these three, is there any reason to deviate from the RAR rankings? Obviously small differences in RAR are not particularly meaningful; on the other hand, if I can’t find a compelling reason to favor one of the candidates, I might as well go with the numbers. Guthrie had a .18 advantage in RA, but this is offset by the additional 29 innings from Dice-K. In eRA, they are basically even (4.33 to 4.27 in Guthrie’s favor), but in FIP, Matsuzaka has a big edge (4.41 to 4.95). Some are always bothered by giving it to a Japanese player who has pitched at a high level for many years. However, the rules state that he is eligible, and I don’t see why not. The ROY is the top newcomer to the major leagues; it need not imply that the man who wins it is wet behind the ears. Since the BBWAA gave many of the early awards to Negro League veterans, it certainly seems as if they felt the same way.

As an additional twist, Matsuzaka at age 27 is actually younger than Guthrie (28), and just a year older than Bannister. I have him atop the starting pitcher heap.

Matsuzaka’s countryman and teammate, Hideki Okajima, is the top rookie reliever (+25, +30, in 69), edging out the Indians’ Rafael Perez. This is not enough to propel him above any of the starters.

Among hitters, there is only one candidate that I find compelling. Names like Delmon Young and Travis Buck may draw consideration, but I see them as inferior in value to the pitchers and to Dustin Pedroia. Pedroia hit pretty well in his rookie campaign, 11 runs better than an average hitter, good for +33 RAR when his position of second base is considered. Obviously defensive value needs to be considered. I am not particularly well qualified to evaluate defensive performance or the relative merits of defensive metrics--I try very hard to understand all of the various offensive evaluation methods, but I simply don’t keep up with the defensive side of things.

That being said, I trust MGL’s Ultimate Zone Rating figures, but try to look at other metrics as well. MGL has only released the top and bottom players at each position for 2007, so figures are not available for most players. In lieu of that, the duel approaches provided by Chone Smith (link goes directly to spreadsheet, or the comparable figures in one category from Jin-AZ) will be the basis for evaluating defense here. Pedroia comes in at a consensus -1, so we can assume that he is an average defensive second baseman.

At +33 RAR and +16 RAA, he trails all of the pitchers in RAR. However, I do slide him ahead of Bannister. Bannister fanned just 4.2 per game, and his 4.84 FIP is well above his actual RA due to his low %H of .266. Thus, I see the AL race as:

1) SP Daisuke Matsuzaka, BOS
2) SP Jeremy Guthrie, BAL
3) 2B Dustin Pedroia, BOS
4) SP Brian Bannister, KC
5) RP Hideki Okajima, BOS

In the National League, the opposite situation holds—the pitching candidates cannot hold up against the wave of batting candidates. There are two tiers of batters, separated by ten RAR--the tier features Ryan Braun (+38 RAA, +54 RAR in 480 PA), Hunter Pence (+20, +39 in 482), and Troy Tulowitzki (+20, +39 in 666). Perhaps the Rockies have made a deal with the devil after all. The second tier includes James Loney (+29 RAR), Kevin Kouzmanoff (+27), Josh Hamilton (+27), and Yunel Escobar (+26).

Focusing on the top candidates, Braun’s mashing to the tune of .322/.366/.631 is truly impressive. Braun led all NL hitters with 300+ PA with that SLG, bettering his teammate Prince Fielder by fifteen points. Such a performance while playing a neutral position like third base would seem to make him a lock for the award.

As has been widely discussed in the sabermetric blogosphere, though, Braun’s defense seems to be truly dreadful. He comes in at -24 in Chone’s consensus and -14 in Chone’s own metric. Factoring this in, his 15 RAR lead over Pence and Tulowitzki is down to nothing.

If Tulowitzki and Pence were average defensive players, then I would still favor Braun, as I have far more confidence in the offensive statistics. That is not the case though. While Pence comes in as dead average in Chone’s figures, Tulowitzki comes out as a defensive star, with a +20 UZR adjusted to 150 games. This turns what would be a pick-em into a no-brainer: Troy Tulowitzki should be the NL Rookie of the Year.

Among pitchers, the top RAR figure was actually turned in by Philly’s Kyle Kendrick (+28), just a head of Tim Lincecum and Yovani Gallardo. One starter who deserves additional consideration is Micah Owings. Despite being just three runs above average and 23 above replacement, he came to the plate 62 times, hitting .333/.349/.683, good for 13 RC in 40 outs. An average pitcher would figure to create around one run in forty outs, so Owings added 12 runs with his bat, pulling up to +36 RAR. While I’m sure he will not maintain this prodigious offensive performance going forward, it had real value in 2007, and so he’ll crack my ballot.

As for the second-tier hitters, they all rate at about -3 defensively, so I’ll take Hamilton because he’s a warm and fuzzy story and played the toughest defensive position:

1) SS Troy Tulowitzki, COL
2) 3B Ryan Braun, MIL
3) CF Hunter Pence, HOU
4) SP Micah Owings, ARI
5) CF Josh Hamilton, CIN

Go Wedge, Go Byrd

I am probably giving the Indians the kiss of death by writing this, but I have been flabbergasted by the some of the bullspit "analysis" I have seen about Game 4 of the ALDS tonight. First, there is an underlying belief that pitching Paul Byrd is tantamount to throwing the game. This is absurd. Byrd is a slightly below average pitcher in my eyes, but he's not a replacement level pitcher either. Sure, his finesse profile does not seem to match up well against the Yankees, but that doesn't mean that he can't beat them in one game. If you had pitcher whose real true talent was allowing 7 runs to the Yanks in 9 innings, and you the Yanks pitcher's real true talent was to allow you just 3.5 (and both are more extreme than the Byrd-Wang matchup actually is), you'd still expect to win 20%.

Second, there is a belief that Wang will pitch extremely well. Why exactly? Wang is a quality pitcher, no doubt, but the Tribe just shelled him on Friday, and he's going on three days rest. Sinkerballers are purported to be better on short rest, but I've never seen a study to back that up. Yes, Wang has pitched better at Yankee Stadium than on the road, but this is hardly prohibitive. Wang should be expected to pitch well, because he is a good pitcher. Expecting him to be unbeatable seems fairly irrational to me.

Third, I have seen one poster/blogger invoke "owing it to your team and your fans to throw your best pitchers at them". A) as a fan of the team myself, I don't feel in anyway cheated; maybe we should have a Bill Veeck grandstand manager routine to figure out who should pitch each game, though. B) How confident are you, really, that Sabathia on three days rest is better than Byrd? Does this level of confidence justify the extra risk induced by pitching Sabathia in a scenario he is not used to? How sure are you, exactly?

C) this stuff about owing it to your team--how about owing it to your team not to panic because you lost one game? What does it say to your team if you announce that you plan to use four starters and proceed in this fashion. Then you win the first two games of the series, but you lose game three. And then panic. What message does that send to your team? "We are a bunch of bums who can't possibly win with Paul Byrd on the mound"? That's how you show confidence and give them the best chance to win?

End of Season Statistics, 2007

For the past several years I have been posting Excel spreadsheets with sabermetric stats like RC for regular players on my website. I have not been doing this because I think it is a unique thing that nobody else does--Hardball Times, Baseball Prospectus, and other sites have similar data available. However, since I figure my own stats for myself anyway, I figured I might as well post it on the net.

This year, I am not putting out Excel spreadsheets, but I will have Google Spreadsheets that I will link to from both this blog and my site. What I wanted to do here is a quick run down of the methodology used.

First, I should acknowledge that the primary data source is Doug’s Stats, and that park data for past seasons comes from KJOK’s park database. The Baseball Direct Scoreboard and ESPN.com round out the sources.

The general philosophy of these stats is to do what is easiest while not being too imprecise, unless you can do something just a little bit more complex and be more precise. This in practice is a subjective standard. For instance, R^2/(R^2 + RA^2) is pretty close, and Pythagenpat is a bit more work, but I used Pythagenpat. On the other hand, using ERP as the run estimator is not optimal--I could, in lieu of having empirical linear weights for 2007, use Base Runs or another approach to generate custom linear weights. I have decided that does not constitute a worthwhile improvement. Others might disagree, and that’s all right. I’m not claiming that any of these numbers are the state of the art or cannot be improved upon.

First, the team report. I list Park Factor (PF), Winning %, Expected Winning % (EW%), Predicted Winning % (PW%), Wins, Losses, Runs, Runs Allowed, Runs Created (RC), Runs Created Allowed (RCA), Runs/Game (R/G), Runs Allowed/Game (RA/G), Runs Created per Game (RCG), and Runs Created Allowed per Game (RCAG):

EW% is based on runs and runs allowed in Pythagenpat, with the exponent = RPG^.29. PW% is based on runs created and runs created allowed in Pythagenpat.

Runs Created and Runs Created Allowed are both based on a simple Base Runs formula. For the offense, the formula is:
A = H + W - HR - CS
B = (2TB - H - 4HR + .05W + 1.5SB)*.76
C = AB - H
D = HR
For the defense:
A = H + W - HR
B = (2TB - H - 4HR + .05W)*.78
C = AB - H (approximated as IP*2.82)
D = HR
Of course, these are both put together, like all BsR, as A*B/(B + C) + D. The only difference between the formulas is that I include SB and CS for the offense, but don’t want to waste time scrounging up stolen bases allowed for the defense.

R/G, RA/G, RCG, and RCAG are all calculated straightforwardly by dividing by games, then park adjusted by dividing by park factor. Ideally, you use outs as the denominator, but for teams, outs and games are so closely related that I don’t think it’s worth the extra effort.

Next, we have park factors. I have explained the methodology used to figure the PFs before, but the cliff’s notes version is that they are based on five years of data when applicable, include both runs scored and allowed, and they are regressed towards average (PF = 1), with the amount of regression varying based on the number of years of data used. There are factors for both runs and home runs. The initial PF (unshown) is:
iPF = (H*T/(R*(T - 1) + H) + 1)/2
where H = RPG in home games, R = RPG in road games, T = # teams in league (14 for AL and 16 for NL). Then the iPF is converted to the PF by taking 1- (1-iPF)*x, where x = .6 if one year of data is used, .7 for 2, .8 for 3, and .9 for 4+.

It is important to note, since there always seems to be confusion about this, that these park factors already incorporate the fact that the average player plays 50% on the road and 50% at home. That is what the adding one and dividing by 2 in the iPF is all about. So if I list Fenway Park with a 1.02 PF, that means that it actually increases RPG by 4%.

In the calculation of the PFs, I did not get picky and take out “home” games, like the three games in Milwaukee and one in Seattle that the Indians played (actually, the Baseball Direct data counted the SEA game as a road game, so there are only three phantom home games). They simply don’t cause that big of a problem. Suppose Jacobs’ Field was a perfectly average park in a league in which there are 4.8 runs/game. At 81 home and road games per year, in the previous four years the Indians and their opponents would have scored 3110.4 runs at home and on the road.

If this season, the Indians played four “home” games in an extreme environment in which say 20 runs were scored per game, they would have 819.2 runs added in to the home total. The road games would contribute 777.6 runs to the five-year total. Now, for the five years the Indians’ home games would have a total of 9.70272 RPG versus 9.6 for the road games. The park factor, when fully figured with the regression factor would be 1.0045, when we know that it should be 1.0000. I’m not going to spend too much time worrying about that kind of discrepancy, and that’s a high end example of what the discrepancy would actually be.

Next is the relief pitchers report. I defined a starting pitcher as one with 15 or more starts. All other pitchers are eligible to be included as a reliever. If a pitcher has 40 appearances, then they are included. Additionally, if a pitcher has 50 innings and less than 50% of his appearances are starts, he is also included here (this allows some swingmen type pitchers who wouldn’t meet either the minimum start or appearance standards to get in).

For all of the player reports, ages are based on simply subtracting their year of birth from 2007. I realize that this is not compatible with how ages are usually listed and so “Age 27” doesn’t necessarily correspond to age 27 as I list it, but it makes everything a heckuva lot easier, and I am more interested in comparing the ages of the players to their contemporaries, for which case it makes very little difference.

Anyway, for relievers, the statistical categories are Games, Innings Pitched, Run Average (RA), Relief Run Average (RRA), Earned Run Average (ERA), Estimated Run Average (eRA), Fielding-Independent Pitching (FIP), Guess-Future (G-F), Inherited Runners per Game (IR/G), Inherited Runs Saved (IRSV), hits per ball in play (%H), Runs Above Average (RAA), and Runs Above Replacement (RAR).

All of the run averages are park adjusted. RA is R*9/IP, and you know ERA. Relief Run Average subtracts IRSV from runs allowed, and thus is (R - IRSV)*9/IP; it was published in By the Numbers by Sky Andrecheck. eRA, FIP, %H, and RAA will be explained in the starters section, and is the invention of Tango Tiger (FIP, that is).

Guess-Future is a JUNK STAT. G-F is A JUNK STAT. I just wanted to make that clear so that no anonymous commentator posts that without any explanation. It is just something that I have used for some time that combines eRA and strikeout rate into a unitless number. As a rule of thumb, anything under 4 is pretty good. I include it not because I think it is meaningful, but because it is a number that I have been looking at for some time and still like to, despite the fact that it is a JUNK STAT. JUNK STATS can be fun as long as you recognize them for what they are. G-F = 4.46 + .095(eRA) - .113(KG), where KG is strikeouts per 9 innings. JUNK STAT JUNK STAT JUNK STAT JUNK STAT JUNK STAT

Inherited Runners per Game is per relief appearance (G - GS); it is an interesting thing to look at, I think. You can see which closers come in with runners on base, and which are used nearly exclusively to start innings. Of course, you can’t infer too much; there are bad relievers who come in with a lot of people on base, not because they are being used in high leverage situations, but because they are long men or what have you. I think it’s interesting, so I include it.

Inherited Runs Saved is the difference between the number of inherited runs the reliever allowed to score, subtracted from the number of inherited runs an average reliever would have allowed to score, given the same number of inherited runners. I do not park adjust this figure. Of course, the way I am doing it is without regard to which base the runners were on, which of course is a very important thing to know. Obviously, with a lot of these reliever measures, if you have access to WPA and LI data and the like, that will probably be more significant.

IRSV = Inherited Runners*League % Stranded - Inherited Runs Scored

Runs Above Replacement is a comparison of the pitcher to a replacement level reliever, which is assumed to be a .450 pitcher, or as I would prefer to say, one who allows runs at 111% of the league average. So the formula is (1.11*N - RRA)*IP/9, where N is league runs/game. Runs Above Average is simply (N - RRA)*IP/9.

On to the starting pitchers. The categories are Innings Pitched, Run Average, ERA, eRA, FIP, KG, G-F, %H, Neutral W% (NW%), Quality Start% (QS%), RAA, and RAR.

The run averages (RA, ERA, eRA, FIP) are all park-adjusted, simply by dividing by park factor.

eRA is figured by plugging the pitcher’s stats into the Base Runs formula above (the one not including SB and CS that is used for estimating team runs allowed), multiplying the estimated runs by nine and dividing by innings. FIP, a DIPS-approximator invented by Tango Tiger, is simply (13*HR + 3*W - 2*K)/IP, plus a constant to make it equal RA on the league level.

Neutral Winning Percentage is the pitcher’s winning percentage adjusted for the quality of his team. It makes the assumption that all teams are perfectly balanced between offense and defense, and then projects what the pitcher’s W% would be on an average team. I do not place a lot of faith in anything based on wins and losses, of course, and particularly not for a one-year sample. In the long run, we would expect pitchers to pitch for fairly balanced teams and for run support for an individual to be the same as for the pitching staff as a whole. For individual seasons, we know that things are not going to even out.

I used to use Run Support to compare a pitcher’s W% to what he would have been expected to earn, but now I have decided that is more trouble than it is worth. RS can be a pain to run down, and I don’t put a lot of stock in the resulting figures anyway. So why bother? NW% = W% - (Mate + .5)/2 +.5, where Mate is (Team Wins - Pitcher Wins)/(Team Decisions - Pitcher Decisions).

Likewise, I include Quality Start Percentage (which of course is just QS/GS) only because my data source (Doug’s Stats) includes them. As for RAA and RAR for starters, RAA = (N - RA)*IP/9, and RAR = (1.25*N - RA)*IP/9.

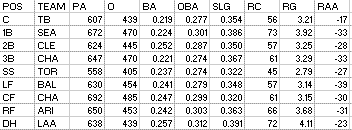
For hitters with 300 or more PA, I list Plate Appearances (PA), Outs (O), Batting Average (BA), On Base Average (OBA), Slugging Average (SLG), Runs Created (RC), Runs Created per Game (RG), Secondary Average (SEC), Speed Unit (SU), Hitting Runs Above Average (HRAA), Runs Above Average (RAA), Hitting Runs Above Replacement (HRAR), and Runs Above Replacement (RAR).

I do not bother to include hit batters, so take note of that for players who do get plunked a lot. Therefore, PA are simply AB + W. Outs are AB - H + CS. BA and SLG you know, but remember that without HB and SF, OBA is just (H + W)/(AB + W). Secondary Average = (TB - H + W)/AB. I have not included net steals as many people (and Bill James himself) does--it is solely hitting events.

The park adjustment method I’ve used for BA, OBA, SLG, and SEC deserves a little bit of explanation. It is based on the same principle as the “Willie Davis method” introduced by Bill James in the New Historical Baseball Abstract. The idea is to deflate all of the positive offensive events by a constant percentage in order to make the new runs created estimate from those stats equal to the park adjusted runs created we get from the player’s actual stats. I based it on the run estimator (ERP) that I use here instead of RC.

X = ((TB + .8H + W - .3AB)/PF + .3(AB - H))/(TB + W + .5H)

X is unique for each player and is the deflator. Then, hits, walks, and total bases are all multiplied by X in order to park adjust them. Outs (AB - H) are held constant, so the new At Bat estimate is AB - H + H*X, which can be rewritten as AB - (1 - X)*H. Thus, we can write BA, OBA, SLG, and SEC as:

BA = H*X/(AB - (1 - X)*H)
OBA = (H + W)*X/(AB - (1 - X)*H + W*X)
SLG = TB*X/(AB - (1 - X)*H)
SEC = SLG - BA + (OBA - BA)/(1 - OBA)

Next up is Runs Created, which as previously mentioned is actually Paul Johnson’s ERP. Ideally, I would use a custom linear weights formula for the given league, but ERP is just so darn simple and close to the mark that it’s hard to pass up. I still use the term “RC” partially as a homage to Bill James (seriously, I really like and respect him even if I’ve said negative things about RC and Win Shares), and also because it is just a good term. I like the thought put in your head when you hear “creating” a run better than “producing”, “manufacturing”, “generating”, etc. to say nothing of names like “equivalent” or “extrapolated” runs. None of that is said to put down the creators of those methods--there just aren’t a lot of good, unique names available. Anyway, RC = (TB + .8H + W + .7SB - CS - .3AB)*.322.

RC are park adjusted, by dividing by PF, making all of the value stats that follow park adjusted as well. RG, the rate, is RC/O*25.5. I do not believe that outs are the proper denominator for an individual rate stat, but I also do not believe that the distortions caused are that bad. (I still intend to finish my rate stat series and discuss all of the options in excruciating detail, but alas you’ll have to take my word for it now).

Speed Unit is my own take on a “speed skill” estimator ala Speed Score. I AM NOT CLAIMING THAT IT IS BETTER THAN SPEED SCORE. I don’t use Speed Score because I always like to make up my own crap whenever possible (while of course recognizing that others did it first and better), because some of the categories aren’t readily available, and because I don’t want to mess with square roots. Anyway, it considers four categories: runs per time on base, stolen base percentage (using Bill James’ technique of adding 3 to the numerator and 7 to the denominator), stolen base frequency (steal attempts per time on base), and triples per ball in play. These are then converted to a pseudo Z-score in each category, and are on a 0-100 scale. I will not reprint the formula here, but I have written about it before here. I AM NOT CLAIMING THAT IT IS BETTER THAN SPEED SCORE. I AM NOT CLAIMING THAT IT IS AS GOOD AS SPEED SCORE.

There are a whopping four categories that compare to a baseline; two for average, two for replacement. Hitting RAA compares to a league average hitter; it is in the vein of Pete Palmer’s Batting Runs. RAA compares to an average hitter at the player’s primary position. Hitting RAR compares to a “replacement level” hitter; RAR compares to a replacement level hitter at the player’s primary position. The formulas are:

HRAA = (RG - N)*O/25.5
RAA = (RG - N*PADJ)*O/25.5
HRAR = (RG - .73*N)*O/25.5
RAR = (RG - .73*N*PADJ)*O/25.5

PADJ is the position adjustment, and it is based on 1992-2001 data. For catchers it is .89; for 1B/DH, 1.19; for 2B, .93; for 3B, 1.01; for SS, .86; for LF/RF, 1.12; and for CF, 1.02.

How do I deal with players who split time between teams? I assign all of their statistics to the team with which they played more, even if this means it is across leagues. This is obviously the lazy way out; the optimal thing would be to look at the performance with the teams separately, and then sum them up.

You can stop reading now if you just want to know how the numbers were calculated. The rest of this post will be of a rambling nature and will discuss the underpinnings behind the choices I have made on matters like park adjustments, positional adjustments, run to win converters, and replacement levels.

First of all, the term “replacement level” is obnoxious, because everyone brings their preconceptions to the table about what that means, and people end up talking past each other. Unfortunately, that ship has sailed, and the term “replacement level” is not going away. Secondly, I am not really a believer in replacement level. I don’t deny that it is a valid concept, or that comparisons to replacement level can be useful for answering certain questions. I just don’t believe that replacement level is clearly the correct baseline. I also don’t believe that it’s clearly NOT the correct baseline, and since most sabermetricians use it, I go along with the crowd in this case.

The way that reads is probably too wishy-washy; I do think that it is PROBABLY the correct choice. There are few things in sabermetrics that I am 100% sure of, though, and this is certainly not one of them.

I have used distinct replacement levels for batters, starters, and relievers. For batters, it is 73% of the league RG, or since replacement levels are often discussed in these terms, a .350 W%. For starters, I used 125% of the league RA or a .390 W%. For relievers, I used 111% of the league RA or a .450 W%. I am certainly not positive that any of these choices are “correct”. I do think that it is extremely important to use different replacement levels for starters and relievers; Tango Tiger convinced me of this last year (he actually uses .380, .380, .470 as his baselines). Relievers have a natural RA advantage over starters, and thus their replacements will as well.

Now, park adjustments. Since I am concerned about the player’s value last season, the proper type of PF to use is definitely one based on runs. Given that, there are still two paths you can go down. One is to park adjust the player’s statistics; the other is to park adjust the league or replacement statistics when you plug in to a RAA or RAR formula. I go with the first option, because it is more useful to have adjusted RC or adjusted RA, ERA, etc. than to only have the value stats adjusted. However, given a certain assumption about the run to win converter, the two approaches are equivalent.

Speaking of those RPW: David Smyth, in his Base Wins methodology, uses RPW = RPG. If the RPG is 9.4, then there are 9.4 runs per win. It is true that if you study marginal RPW for teams, the relationship is not linear. However, if you back up from the team and consider things in league context, one can make the case that the proper approach is the simple RPW = RPG.

Given that RPW = RPG, the two park factor approaches are equivalent. Suppose that we have a player in an extreme park (PF = 1.15, approximately like Coors Field) who has a 8 RG before adjusting for park while making 350 outs in a 4.5 N league. The first method of park adjustment, the one I use, converts his value into a neutral park, so his RG is now 8/1.15 = 6.957. We can now compare him directly to the league average:

RAA = (6.957 - 4.5)*350/25.5 = +33.72

The second method would be to adjust the league context. If N = 4.5, then the average player in this park will create 4.5*1.15 = 5.175 runs. Now, to figure RAA, we can use the unadjusted RG of 8:

RAA = (8 - 5.175)*350/25.5 = +38.77

These are not the same, as you can obviously see. The reason for this is that they are in two different contexts. The first figure is in a 9 RPG (2*4.5) context; the second figure is in a 10.35 RPG (2*4.5*1.15) context. Runs have different values in different contexts; that is why we have RPW converters. If we convert to WAA, then we have:

WAA = 33.72/9 = +3.75
WAA = 38.77/10.35 = +3.75

Once you convert to wins, the two approaches are equivalent. This is another advantage for the first approach: since after park adjusting, everyone in the league is in the same context, there is no need to convert to wins at all. Sure, you can convert to wins if you want. If you want to compare to performances from other seasons and other leagues, then you need to. But if all you want to do is compare David Wright to Prince Fielder to Hanley Ramirez, there is no need to convert to wins. Personally, I think that stating something as +34 is a lot nicer than stating it as +3.8, if you can get away with it. None of this is to deny that wins are not the ultimate currency, but runs are directly related to wins, and so there is no difference in conclusion from using them if the RPW is the same for all players, which it is for a given league season coupled with park adjusting runs rather than context.

Finally, there is the matter of position adjustments. What I have done is apply an offensive positional adjustment to set a baseline for each player. A second baseman’s RAA will be figured by comparing his RG to 93% of the league average, while a third baseman’s will compare to 101%, etc. Replacement level is set at 73% of the estimated average for each position.

So what I am doing is comparing to a “replacement hitter at position”. As Tango Tiger has pointed out, there is really no such thing as a “replacement hitter” or a “replacement fielder”--there are just replacement players. Every player is chosen because his total value, both hitting and fielding, is sufficient to justify his inclusion on the team. Segmenting it into hitting and fielding replacements is not realistic and causes mass confusion.

That being said, using “replacement hitter at position” does not cause too many distortions. It is not theoretically correct, but it is practically powerful. For one thing, most players, even those at key defensive positions, are chosen first and foremost for their offense. Empirical work by Keith Woolner has shown that the replacement level hitting performance is about the same for every position, relative to the positional average.

The offensive positional adjustment makes the inherent assumption that the average player at each position is equally valuable. I think that this is close to being true, but it is not quite true. The ideal approach would be to use a defensive positional adjustment, since the real difference between a first baseman and a shortstop is their defensive value. When you bat, all runs count the same, whether you create them as a first baseman or as a shortstop.

Figuring what the defensive positional adjustment should be, though, is easier said than done. Therefore, I use the offensive positional adjustment. So if you want to criticize that choice, or criticize the numbers that result, be my guess. But do not claim that I am holding this up as the correct analytical structure. I am holding it up as the most simple and straightforward structure that conforms to reality reasonably well, and because while the numbers may be flawed, they are at least based on an objective formula. If you feel comfortable with some other assumptions, please feel free to ignore mine.

One other note here is that since the offensive PADJ is a proxy for average defensive value by position, ideally it would be applied by tying it to defensive playing time. I have done it by outs, though. For example, shortstops have a PADJ of .86. If we assume that an average full-time player makes 10% of his team’s outs (about 408 for a 162 game season with 25.5 O/G) and the league has a 4.75 N, the average shortstop is getting an adjustment of (1 - .86)*4.75/25.5*408 = +10.6 runs. However, I am distributing it based on player outs. If you have one shortstop who makes 350 outs and another who makes 425 outs, then the first player will be getting 9.1 runs while the second will be getting 11.1 runs, despite the fact that they may both be full-time players.

The reason I have taken this flawed path is because 1) it ties the position adjustment directly into the RAR formula rather then leaving it as something to subtract on the outside and more importantly 2) there’s no straightforward way to do it. The best would probably be to use defensive innings--set the full-time player to X defensive innings, figure how Derek Jeter’s innings compare to X, and adjust his PADJ accordingly. Games in the field or games played are dicey because they can cause distortion for defensive replacements. Plate Appearances avoid the problem that outs have of being highly related to player quality, but they still have the illogic of basing it on offensive playing time. And of course the differences here are going to be fairly small (a few runs). That is not to say that this way is preferable, but it’s not horrible either, at least as far as I can tell.

Given the inherent assumption of the offensive PADJ that all positions are equally valuable, once we have a player’s RAR, we should account for his defensive value by adding on his runs above average relative to a player at his own position. If there is a shortstop out there who is -2 runs defensively versus an average shortstop, he is without a doubt a plus defensive player, and a more valuable defensive player than a first baseman who was +1 run better than an average first baseman. Regardless, since we have implicitly assumed that they are both average defensively for their position when RAR was calculated, the shortstop will see his value docked two runs. This DOES NOT MEAN that the shortstop has been penalized for his defense. The whole process of accounting for positional differences, going from hitting RAR to positional RAR, has benefited him.

It is with some misgivings that I publish “hitting RAR” at all, since I have already stated that there is no such thing as a replacement level hitter. It is useful to provide a low baseline total offensive evaluation that does not include position, though, and it can also be thought of as the theoretical value above replacement in a world in which nobody plays defense at all.

The DH is a special case, and it caused a lot of confusion when my MVP post was linked at BTF last year. Some of that confusion has to do with assuming that any runs above replacement methodology is the same as VORP from the Baseball Prospectus. Obviously there are similarities between my approach and VORP, but there also key differences. One key difference is that I use a better run estimator. Simple, humble old ERP is, in my opinion, a superior estimator to the complex MLV. I agree with almost all of the logic behind MLV--but using James’ Runs Created as the estimator to fuel it is putting lipstick on a pig.

The big difference, though, as it relates to the DH, is that VORP considers the DH to be a unique position, and I consider DHs as in the same pool as first baseman. The fact of the matter is that first baseman outhit DH. There are any number of potential explanations for this; DHs are often old or injured, hitting as a DH is harder than hitting as a position player, etc. Anyway, the exact procedure for VORP is propriety, but it is apparent that they use some sort of average DH production to set the DH replacement level. This makes the replacement level for a DH lower than the replacement level for a first baseman.

A couple of the aforementioned nimrods took the fact that VORP did this and assumed that my figures did as well. What I do is evaluate 1B and DH against the same replacement RG. This actually helps first baseman, since the DHs drag the average production of the pool down, thus resulting in a lower replacement level than I would get if I considered first baseman on their own. Contrary to what the chief nimrod thought, this is not “treating a 1B as a DH”. It is “treating a 1B as a 1B/DH”.

It is true, however, that this method assumes that a 1B and a DH have equal defensive value. Obviously, a DH has no defensive value. What I advocate to correct this is to treat a DH as a bad defensive first baseman, and thus knock another five or ten runs off of his RAR for a full-time player. I do not incorporate this into the published numbers, but you should keep it in mind. However, there is no need to adjust the figures for first baseman upwards, despite what the nimrods might think. The simple fact of the matter is that first baseman get higher RAR figures by being pooled with the DHs than they would otherwise.

2007 Park Factors

2007 Leagues

2007 Teams

2007 AL Relievers

2007 NL Relievers

2007 AL Starters

2007 NL Starters

2007 AL Hitters


2007 NL Hitters