In this installment, I will look at the accuracy of the formulas we have created compared to the accuracy of some other run estimators. Let me pile on some caveats here:
1. I am certainly not claiming that accuracy in terms of RMSE on actual major league teams is the only standard by which to evaluate a run estimator, or even the most important. It is something interesting to look at.
2. The data used for the test is 1990-2005, except 1994. This overlaps with the sample data we used to derive our formulas, giving them an inherent advantage. This should be considered when looking at the results.
3. A corollary to #1, it must always be remembered that there is correlation between the various offensive events. A category like SF, which guarantees that a run has been scored, can be treated in a way such that it increases the accuracy of a formula, but decreases its accuracy in application to players and in theory. It has always been a source of amusement for me that there is somewhat of an overlap between the crowd that claims run estimators are subject to the ecological fallacy and the crowd that exalts lowest RMSE above all other virtues.
First, I will compare a group of estimators that only use the basic statistics (AB, H, D, T, HR, W, SB, and CS). This includes Bill James’ Stolen Base RC (RC), Jim Furtado’s Extrapolated Runs Basic (XR) , a variant of Paul Johnson’s ERP (ERP), the basic LW introduced in the first part of this series from Ruane’s data (LW-R), the older BsR version that I have used (Old BsR), the two BsR versions introduced in the second installment (B1 and B2), the two simple BsR versions from David Smyth introduced in the last installment (sBsR1 and sBsR2; remember that these do not use SB or CS) and two regression equations (Reg1 and 2, formulas at the bottom of the post).
I have included two measures of accuracy: RMSE and average percentage error ABS(R-RC)/R:
I’m a little disappointed that the new BsR formulas came out worse than the old one, but I’m not sure what data I calibrated that one on. Of course, the new versions benefited at least a bit from this phenomenon too. Again, to really do a fair test, you would have to test on data outside of the sample used to create the formula. I should do that, but I have done those kinds of tests before. My goal here is not to show which estimator is the “best”, even within the sphere of RMSE analysis.
It is also true, as David Smyth pointed out in a discussion on The Book Blog, that the weights which return the “correct” linear weights values are not necessarily those that will be most accurate for estimating team runs for normal teams. This could be even more of a factor when the linear weights themselves have been adjusted to equal total runs scored, as they have not accounted for all of the possible outcomes (for example, Ruane’s linear weights ignore reached on error, wild pitches, and several other events). This is why I in no ways intend the formula here to supercede Tango Tiger’s full Base Runs equation and corresponding linear weights. These are simply BsR versions that utilize the full complement of official statistics while considering nothing beyond those.
The regression equations come in front, which they should, considering that they are specifically tailored to work with the 430 unique batting lines in this sample. The formulas for them are in the bottom section and I’ll repeat myself again on regression there.
With that aside, let’s move on to looking at estimators that take advantage of all of the official offensive categories. Here, we have ERP again; Bill James’ Tech-1 RC, HDG-24 RC, and revised RC; another old BsR version of mine; LW-R, the weights we derived in part one from Ruane’s study; “RC match”, which is RC with B weights to match the target weights; “CR match”, which is loosely based on Eric Van’s Contextual Runs framework and also matches the target weights; and the Full-1 through 4 BsR versions introduced in part two (plus the F-1 version with a corrected walk coefficient):
Again, the regression equations win out as they should. My older BsR version does better than the new ones, which makes me suspect that I calibrated it on a dataset that heavily overlapped this one. While I introduced four new BsR equations here, they were all almost exactly the same when applied to these real teams. The “winner”, Full-2, is one based on initial baserunners and all outs, for what it’s worth, which is not a lot. The choice of which version to use should be based on how they would do theoretically and how their weights stack up rather than which had a RMSE .02 lower than the others.
One thing to note is that James’ Tech-1 RC formula is not particularly accurate, at all, at least for recent years. Stolen Base RC, despite ignoring IW, SH, SF, DP, and HB, has a RMSE nearly three runs lower than Tech-1. James himself does not use Tech-1 anymore; he supplanted it first with the HDG-24 formula and than with the one he uses now that doesn’t have a catchy name. However, some folks out there still use Tech-1, and even if you are not concerned about all of the issues that have been raised about the RC model itself, you should recognize that Tech-1 is a poor estimator.
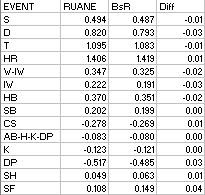
Since we have Ruane’s empirical weights, it would be interesting to compare the BsR-generated weights for various seasons. I did not do a comprehensive analysis, but I did take a look at two extreme leagues (the 1968 NL and the 1996 AL; of course, “extreme” on the league level is nothing like extreme on the team or, to an even greater degree, the player level). Again, this is not in anyway intended to be a conclusive study, it is just an interesting platform to use for further discussion. I used the Full-1 version of BsR (initial baserunners, batting outs) to generate the BsR values:
1968 NL:
1996
The BsR intrinsic weights are within .03 runs for each event except the triple in 1968 and the sac fly in both seasons. Perhaps the high B weight for the triple keeps the coefficient artificially high even in low run environments. In the case of the sac fly, Base Runs weights it nearly equally in 1968 and in 1996. Apparently, my treatment of the event does not allow its value to fluctuate as much as it actually does. Perhaps treating it as a removed baserunner would do the trick, although if you do that you pretty much have to count it as a guaranteed run to balance things out, and I don’t like the implications of that. If I had my druthers, the official stats would give us breakdowns for flyouts and groundouts instead of the subcategories of SF and DP, and then this wouldn’t be an issue at all.
Miscellaneous Formulas
Full ERP = (TB + .792H + W + HB - .5IW + .3SH + .7(SF + SB - DP) - CS - .292AB - .031K)*.322
This is one I had sitting around from years ago; it obviously does not properly value the events, but that’s part of the reason why I included it--its accuracy with real teams is not that far off from the others, despite having some obvious flaws. Let it serve as another example about the limitations of RMSE.
Reg-1 = .222H + .302TB + .336W + .242SB - .177CS - .113(AB - H)
Reg-2 = .553S + .705D + 1.117T + 1.499HR + .330W + .240SB - .215CS - .113(AB - H)
Reg-3 = .225H + .290TB + .366W - .336IW + .267HB + .151SB - .121CS + .640SF + .001SH - .100(AB - H) - .020K - .379DP
Reg-4 = .552S + .645D + .993T + 1.458HR + .353W - .287IW + .346HB + .144SB - .141CS + .715SF - .026SH - .101(AB - H - K - DP) - .117K - .475DPTake a look at how the third and fourth formulas treat the double. The formula that considers the hit types separately weight the double at .65 runs, while the version that uses hits and total bases weight it at .81 runs. The dataset used was exactly the same; the only difference is the variables that were fed into the regression. We would expect to have a slight discrepancy between the value of an extra base hit from the approach of valuing each extra base equally. But a .16 run gap? Some of it is the product of adding the sacrifice fly, some of it is just the fact that the inputs are different and the mathematical procedure does not know anything about baseball. The fact that such a difference can occur for the same dataset should illustrate to anyone who still places a large amount of faith in regression equations for the job of estimating event values that it may be a misguided faith.
If you are concerned about the ecological fallacy, regressions are the methods that you should worry about. The best example is the sacrifice fly. From Ruane’s data, it is apparent that at the average scoring level of 1960-2004, the sacrifice fly is a neutral play from a run expectancy standpoint (-.01 runs). When that value is converted to absolute runs, it is worth about +.15 runs.
However, regression procedures know nothing about baseball reality. They only know about the combinations of numbers you give them, and the correlation between the variables. Sacrifice flies correlate decently with runs scored (better than triples, hit batters, or steals in this sample), and each sac fly is a guaranteed run for the team. You can see that the sac fly is evaluated as being worth more than a double, which is absurd on its face.The double is also only .1 runs more valuable than a single in the regression equation.
"Old" BsR Formulas:
A = H + W - HR - CS
B = (2TB - H - 4HR + .05W + 1.5SB)*.76



Patriot: good stuff. Note that the table name for the AL is showing the wrong year...
ReplyDeleteThanks
ReplyDelete