Run Distribution and W%, 2009

There are a lot of ways to look at team performance based on margin of victory, runs scored in a game, runs allowed in a game, and a like. In this post I look at a few. It is by no means intended to be a comprehensive examination. The data is from Baseball Prospectus, where you can download it very easily and import it to a spreadsheet.

First, let's look at team performance broken down by run differential for the game. I break games into three categories: one-run games, blowout games (margin of five or more), and other games, which for lack of a better team I'll call middle games. You can certainly quibble with the definition of a blowout, but I like the cutoff at five run because it results in the frequency of one-run games and blowouts being approximately equal.

It is necessary to note (and, embarrassingly, I didn't last year) that any run distribution based on games is subject to the bottom of the ninth/extra inning problem--home team scoring is capped in those innings, or home teams don't bat in those innings at all. The analysis that follows assumes that this impacts all teams equally, but that is not necessarily the case. So keep that thought in the back of your mind if you choose to read what follows.

First up are one-run games. There were 656 one-run games in the majors in 2009, out of 2430 total games (27%). Seattle had the highest frequency (34%) and Pittsburgh the lowest (21%). The table below is sorted by the difference between W% in one-run game and W% in all other games:



The eight playoff participants (who I'll use as a stand-in for quality teams in this piece, although it is somewhat circular) had a combined .556 one-run record and a .590 record in other games. These teams played in one-run games 27% of the time, the same as the league average. Six of the eight playoff teams had lower W%s in one-run games than other games (the Angels and Twins were the exceptions, and .016 was the largest difference). It is of course well-known that one-run records are pulled towards .500 for teams of at all observed W% levels.

Again, I've defined blowout games as those determined by five or more runs. There were 686 such games (28%). Kansas City played in the most (36%) and the Mets the least (23%):



Once again, playoff teams played in blowouts with about the same frequency as other clubs (29%). Five of eight had better records in blowouts than other games, with the Yankees (-.016) displaying the largest dropoff. The playoff teams had a composite .619 record in blowouts versus .565 in other games.

You will notice that the Padres had the largest absolute difference by far, going just 10-32 in blowouts but winning a very respectable 54.2% of non-blowouts.

That leaves the "middle" games--and if you have a catchy idea about what to call them, I'd love to hear it--games determined by 2-4 runs. There were 1088 such games, representing 45% of all big league games. Pittsburgh played in the most (51%) and Kansas City the least (38%):



44% of playoff participants' games were middle games, and they recorded a .570 W% compared to .589 in other games. Two of eight (Yankees and Phillies) had better records in middle games, while Colorado was just about even.

Switching gears, here are the frequencies with which teams scored X runs in a game, along with their W% in those games. I'd run a runs allowed frequency list, but of course it will be the same with the exception of complementary W%s:



The mode is three runs (14.2% of games). The "marg" column shows the marginal increase in observed W% for each additional run scored (I cut it off at ten as the frequencies are not very high). You can see that the most valuable run was the fourth, with a jump from a .337 W% to .523. When teams scored three or fewer runs (which occurred 41.9% of the time), they were 393-1644 (.193); when scoring four or more (58.1% frequency), they were 2037-786 (.722).

Last year, I applied a Jamesian concept of Offensive W% based on team run distribution, and will do so again. However, I will not walk through all of the math in detail, and instead will point you to last year's post if you are interested.

The proposed James approach, which I labeled gOW% for "game" Offensive W%, uses the actual W%s for each X runs scored. Of course, one could attempt to model a theoretical W% for each X rather than using the empirical 2009 data. The former would be preferable, but I don't intend this to be taken as a deadly serious exercise so I will stick with the empirical 2009 data, which is subject to the whims of sample size (we are also ignoring the difference in scoring level between the two leagues). I have also lumped all games with ten or more runs scored together at a W% of .955.

Just to make this clear, if a team was shutout 20% of the time, scored one run 30% of the time, and scored two runs 50% of the time (obviously a ridiculous scenario), their gOW% for 2009 would be:

.20(0) + .30(.075) + .50(.208) = .127

I have also figured a standard OW%, holding the defense's RA/G at the league average of 4.61 R/G and using Pythagenpat (there are no park factors applied to any of the results in this post). The traditional OW% and gOW% are usually quite close, as we should expect; when they differ, that means that the run distribution of the team diverged from the expected distribution. Positive differences of gOW% minus OW% indicate teams that bunched their scoring more efficiently than Pyth expected; negative differences indicate an inefficient distribution (keeping the caveat about the ninth inning from the beginning of the post in mind). So, here are a list of teams whose gOW% and OW% differ by more than two games (prorated to 162):

Positive difference: SEA, NYN, SD, CIN
Negative difference: TB

The four teams with higher than expected gOW%s were all bad offenses; none had a gOW% higher than .467. Only one team had a two game negative difference, but the Rays still had a good offense (.521 gOW%), and the next seven teams on the list were all above .500 in that category as well.

We can of course turn this procedure around and use it to calculate gDW%, and standard DW%. The teams with differences of more than two games/162 between the two were:

Positive difference: NYA, KC
Negative difference: LA, PHI, TOR

Finally, we can combine gOW% and gDW% to get what I call gEW%, and compare that to either actual W% or EW% figured from Pythagenpat. The details of the gEW% calculation are given in last year's linked post.

It is not particularly interesting to compare gEW% to actual W%, as most of the biggest differences will occur when teams wins were out of line with expectations based on runs and runs allowed--whether you consider runs in the aggregate (standard EW%) or on the game level (gEW%). Instead, I will list the teams with differences of two games or more per 162 games between gEW% and EW%:

Positive difference: NYA, KC, CIN, HOU, NYN, SEA, SD
Negative difference: LA, PHI, TB, TOR, ATL

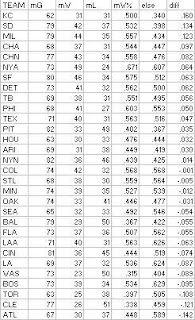
Here are the six discussed W% estimates for all teams, sorted by gEW%: