Run Distribution and W%, 2010

A couple of caveats apply to everything that follows in this post. The first is that there are no park adjustments anywhere. There's obviously a difference between scoring 5 runs at Petco and scoring 5 runs at Coors, but if you're using discrete data there's not much that can be done about it unless you want to use a different distribution for every possible context. Similarly, it's necessary to acknowledge that games do not always consist of nine innings; again, it's tough to do anything about this while maintaining your sanity.

All of the conversions of runs to wins are based only on 2010 data. Ideally, I would use an appropriate distribution for runs per game based on average R/G, but I've taken the lazy way out and used the empirical data for 2010 only.

This post also contains little in the way of "analysis" and a lot of tables. This is probably a good thing for you as the reader, but I felt obliged to warn you anyway.

I've run a post like this in each of the last two years, and I always started with an examination of team record in one-run, blowout (5+ margin), and other (2-4 run margin) games. While I was aware of the havoc that bottom of the ninth/extra innings can unleash on one-run records, I have to admit that I was understating the impact, and thus giving a lot more attention to one-run records than they deserved. So this year I've made it simple with two classes: blowouts (5+ margin) and non-blowout (margin of 4 or less).

72.6% of games are non-blowouts; 27.4% are blowouts. Of course, "blowout" is not an appropriate description for many five run games, but I've got to call it something. Team records in non-blowouts:



The standard deviation of W% in non-blowouts is .050, compared to .068 for all games and .138 for blowouts. Blowout records:



The much wider range is easy to see. The next chart shows each team's percentage of non-blowouts and blowouts, as well as the difference in W% between the two classes (figured as blowout W% minus non-blowout W%):



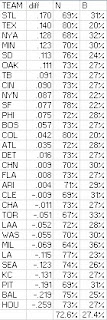
Colorado had the fewest blowouts, with only 20%, which is a bit of an oddity as a strong hitter's park increases the likelihood of a blowout (obviously team quality is a strong factor as well). Milwaukee led the way with 36% blowouts, and while their 25 blowout wins tied for tenth, their 33 blowout losses trailed only the Pirates.

Anyone who reads this blog doesn't need the reminder, but a quick perusal of this list should remind you that the notion that good teams make their hay by winning close games is bunk. Good teams have better record in blowout games than non-blowout games as a rule. Even a team like San Francisco which did not have many blowouts (only 22%) had a strong record (22-13) when they did find themselves in such a contest.

Blowouts/non-blowouts is not a very granular way of looking at margin of victory data; they simply divide all victory margins into two classes. This chart shows the percentage of games decided by X runs, and the cumulative percentage of games decided by less than or equal to X runs:



The most common margin was one run, and each successive margin was less frequent than its predecessor (except for sixteen, and by that point so what?) About half of games were decided by two runs or less, and about 10% were by seven runs or more.

Team runs scored and allowed in wins and losses can serve as interesting tidbits, and as a reminder that there is nothing unusual about having a large split between performance in wins and performance in losses. First, here are team runs scored for wins and losses, along with the ratio of each to the team's overall scoring average:



The average team scored 6.06 in their wins, which is 139% of the overall average; in losses the average is 2.69 runs, or 62% of average.

Runs allowed in wins and losses:



Another application for the data is the average margin of victory for each team. The chart that follows lists each team's average run differential in wins (W RD); losses (L RD); and the weighted average of the two (absolute value--otherwise we'd have plain old run differential). The average margin of victory was 3.41 runs:



The White Sox were the model team, with their winning and losing margins both scoring direct hits on the league average. The Yankees had the highest run differential in wins (3.93), while Baltimore had the lowest (2.51). High losing margins congregated in the NL Central, as Pittsburgh, Milwaukee, Houston, and Chicago were all at or just below four and lost by .22 runs more than fifth-ranking Kansas City. In what is just a coincidence, Texas and San Francisco had the smallest average losing margins; the Rockies and Rays joined them in keeping losses under three runs/game.

Texas' average game was the closest in the majors (3.02 differential). Milwaukee was on the other extreme, with their 4.00 margin easily the highest in the majors. I would figure the medians, but a column filled with 3s wouldn't be very interesting.

I will now shift gears from margins of victory to counts of runs scored and allowed in games. For a manageable look at the data, I've split games into three classes. Low scoring games are those in which a team scores 0-2 runs; 30.6% of 2010 games fell into this class, and teams had a .144 W%. Medium scoring games are 3-5 runs, representing 38% of games and a .503 W%. High scoring games feature 6+ runs, occurring 31.4% of the time with teams winning at a .844 clip.

These classifications are nice because they are somewhat symmetric. Each category contains roughly 1/3 of games (that might be too strong, but it's the best one can do), and medium games are very close to a .500 W%, with low and high scoring games having roughly complementary W%s. Of course, it doesn't work out so neatly when the run environment is more extreme. 2010's 4.38 R/G average was pretty standard, but if you look at a season like 1996 (5.04 R/G), things don't work out as nicely: 24.3% low-scoring (.123 W%), 37.5% medium-scoring (.441), and 38.2% high-scoring (.798).

Caveats aside, here are the game type frequencies by team:



I'll let you peruse these tables for whatever tidbits you might find, because at this point it's no longer sporting to point and laugh at the Mariners, and it largely corresponds to what you already know about team offense. The same holds for the flip side--runs allowed broken down into low, medium, and high:



Of course, teams had a .856 W% in games in which they hold their opponents to a low score, .497 in medium games, and .156 in high-scoring games.

We could also look at teams records in games by scoring class. This chart shows team records in games grouped by runs scored:



To the extent that this data tells you anything, it tells you more about the opposite unit (defense in this case). It has a lot more use as trivia than analytical fodder. Detroit was 1-37 (.026) in games in which they scored 0-2 runs, while Philadelphia was 13-38 (.255) in such contests. Even when Seattle had a high-scoring game, they didn't clean up to the extent that other teams did (19-6, .760).

I found a few of the factoids in the reverse (record in games grouped by runs allowed) a little more interesting:



Boston (42-1, .977) and Baltimore (28-1, .966) were heads and shoulders above the rest of the teams when holding opponents to a low-scoring game--the next fewest number of losses was four, with the Yankees having the most wins with four losses. Even allowing a moderate number of runs spelled doom for the Mariners, as they were just 16-40 (.286) when allowing 3-5 runs; Pittsburgh's 22-38 looked good in comparison.

The Mariners' performance when allowing six or more runs was something else entirely: 1-53 (.019). What's odd is that Cincinnati, despite having a good offense, was the next worst team when allowing a lot of runs (1-31, .031). Philadelphia and Boston each managed to slug their way to a .304 W% in those games, meaning that Boston was the top-performing team both when their defense sparkled (42-1 in low scoring games) and when it was poor. It was a pedestrian record in the middle RA games (30-33) that held the Red Sox back.

I'll close with the most useful analytical tools in the article--what I call game Offensive W% (gOW%), game Defensive W% (gDW%), and game expected W% (gEW%). These metrics are based on a Bill James construct from the 1986 Abstract to evaluate teams based on their actual runs distribution. Instead of using the Pythagorean formula to estimate a team's W% assuming the other unit was average, he proposed multiplying the frequency of each runs scored level by the overall W% in those games. The resulting unit is the same as classic OW%, but it is based on the run distribution rather than the run average.

In order to figure gOW% (and the other metrics), one first needs an estimate for W% at each runs scored level. The empirical data for 2010:



The "marg" column shows the marginal benefit of each additional run; going from one to two runs increases W% by .122. Each run is incrementally more valuable through four, and then the benefit begins to decline, although this year's results have a blip in which the sixth run had a higher marginal impact than the fifth run.

The column marked "use" is the value I used to figure gOW% for each runs scored level. To smooth things out (crudely so, but nevertheless assuring that each additional run either left unchanged or increased the win estimate), I averaged the results for 9-12 runs per game. The "invuse" column is the complement of those values, which are used to figure gDW%. A more comprehensive explanation about how all of the W%s are calculated is included in the 2008 edition of this post.

For most teams, gOW% and OW% (that is, estimates of offensive strength based on run distribution and average runs/game respectively) are very similar. Teams gOW% higher than OW% distributed their runs more efficiently (at least to the extent that the methodology captures reality; there are other factors including park effects, non-uniform inning games, covariance between runs scored and allowed, and failure of the empirical estimates of W% for each runs scored value); the reverse is true for teams with gOW% lower than OW%. The teams that had differences of +/- 2 wins between the two metrics were:

Positive: SEA, HOU, BAL, CLE, OAK
Negative: PHI, COL

You'll note that the positive differences tended to belong to bad offenses; this is a natural result of the nature of the game, and is reflected in the marginal value of each run as discussed above. Runs scored in a game are not normally distributed because of the floor at zero runs, and once you get to seven runs you'll win 80% of the time with average pitching, so additional runs have much less win impact.

The teams for which gDW% was out of sync with DW% by two or more games:

Positive: CHN
Negative: SF, BAL, TEX, NYA

Both pennant winners had inefficient distributions of runs allowed, but it obviously didn't hurt them too much. San Francisco's gDW% of .572 was still good for second in the majors behind San Diego, which had a similarly inefficient runs allowed distribution (although not quite extreme enough to make the above list).

gOW% and gDW% can be combined with a little Pythagorean manipulation to create gEW%, which is a measure of expected team W% based on runs scored and allowed distributions (treating the two as if they are fully independent). The teams which had two game deviations between the two estimates:

Positive: HOU, CHN, SEA, KC, NYN
Negative: SF, PHI, NYA, TEX, COL, SD

This happened to break down pretty clearly into a good team/bad team dichotomy, but that is not always the case. gEW% had a lower RMSE in predicting actual team W% than did EW% (2.63 to 2.83), which is not as impressive of a feat as it might sound. Given that gEW% gets the added benefit of utilizing run distribution data rather than aggregate runs scored, a tendency to under-perform EW% would be indicative of a serious construction flaw. In any event, both RMSEs for 2010 were well below the usual error for a R/RA W% estimated, which is generally in the neighborhood of f our games, which tells us nothing but as a long-time user and constructor of W% estimators, it certainly caught my eye.

Here is the full chart for the game and standard W%s discussed above, sorted by gEW%: