Tripod: Common Fallacies

See the first paragraph of this post for an explanation of this series.

Here I deal with some misinformation that is sometimes spread about sabermetrics, or poorly designed statistical methods that are against sabermetric principles. The most important things to remember about sabermetrics are 1) that it is not the numbers themselves that matter, it is what the numbers mean and 2) the only thing that matter is wins, and the only things that lead to wins are runs and outs. Those two principles serve to explain most of the folly behind these fallacies.

The "Bases" Fallacy

There are many methods proposed, by many different people, that use bases and outs as the two main components. These include Boswell's Total Average, Offense Ratio, Codell's Base Out Percentage. There are others too, either looking at bases/out or bases/PA. Not all of the people who have designed these methods fall into the fallacy. Specifically I'll look at John McCarthy and his 1994 book from Betterway Books, Baseball's All-Time Dream Team.

McCarthy rates the great players of all time by what he calls the Earned Bases Average. EBA = (TB + W + SB - CS)/(AB + W). McCarthy mentions that he has read the sabermetric research, but that the sabermetric work is too difficult for the average fan to understand. He goes on to talk about how Linear Weights puts a HR as 3.15 times more valuable than a single, a triple 2.2, a double 1.7, and so on. He then says, "I believe that the value of a baseball game is more than just runs and winning. Winning is the player's aim, but there is also a transcendent beauty to great hits. It is that beauty that puts fans into the seats and visions of grandeur into kids' fantasies. A home can immeasurably lift the spirits of the team, or take the wind out of opponents. So I challenge a mathematical concept which devalues the extra bases earned by sluggers and speedsters."

Now, Mr. McCarthy may indeed have a point when he speaks of "grandeur" and stuff like that. It is OK if you want to design a method to measure the grandeur of players. Just don't get that confused with what actually wins baseball games. He later explains that the estimated values are not "tangible or real", and that "they are too complicated and many times are just clearly wrong." Sorry, buddy, it is you who are clearly wrong. A baseball game is not played in a vacuum. A player must interact with his teammates. The situations that occur by runners and outs effect the value of offensive events. Sure they are not always constant. That is why you must decide what you are measuring, be it ability or value, and choose value added runs or context neutral runs. But the fact is, a home run is not four times more valuable than a single. It just isn't. And a stolen base is clearly not as valuable as a single, because it advances just one baserunner by one base, whereas a single advances the hitter by one base, and advances most runners by at least one and sometimes two bases. Plus it gives an extra Plate Appearance to the team's offense. A stolen base does none of this.

The basic problem with McCarthy's thinking is that bases are not what matters. The game may be called baseball, but the winner is not the one with the most bases but the one with the most runs. You must relate everything to run scoring eventually if you want to really approximate its value. And TA and EBA and the like can be decent estimators of runs. But all bases are not created equal. A SB is worth always at least one base and a HR at least four. But a SB can only be worth one base and a HR can be worth as many as ten bases. The EBA concept is assuming that the only bases that matter are the one that individual genereates for himself, but again, no player is an island. Everything eventually comes down to runs and outs, not bases.

The Right-Handed Hitter Adjustment Fallacy

This is one that you can try to sneak by people. After all, sabermetricians seeming like to adjust for everything, whether or not it needs to be adjusted for, right? So, since there are more right-handed pitchers than southpaws, and righties hit worse versus righties, shouldn't they get credit for dealing with this disadvantage? No way, Jose.

Well, I suppose that if you want to measure literal ability, you want a right handed adjustment. But literal ability had nothing to do with winning baseball games. It has to do with batting practice and skills competitions, and jaw dropping, but not winning. Just as, because of the dynamics of baseball, not all bases are created equal, a lefty hitter is worth more than a righty of the same literal ability, assuming the normal left/right effect holds for them both. I view this extra credit for righties as tantamount to giving credit for ability to play the banjo. I mean, if I had a clone, the same as me in every way, except he could play the banjo and I couldn't, that would make him a more interesting guy than me, no? Sure. What does playing the banjo have to do with winning baseball games? About the same amount as being right-handed.

Seriously, being a right-handed hitter in baseball is a small handicap, just as being unable to hit home runs is a handicap, and having an 85 mph fastball is not as good as a 90 mph fastball. It is a great deal like if we gave Muggsy Bouges extra credit for being 5"5. That certainly hurts his stats, so why don't we adjust for it? Because it's a fact of life that these things are disadvantages, and the goal of baseball is to win games, not to look good.

Here is an example of a biased man who manipulates the numbers in this way. Giving Jim Rice 73% of his PAs vs. lefties is stupid, because 73% of the plate appearances pitched in baseball are not by lefty pitchers.

The Fallacy of the Ecological Fallacy

From time to time, someone who has a background in formal statistics will claim that applying various measures tested at the team-level to individual players(usually a run estimator) is falling prey to the Ecological Fallacy and is thus invalid.

Not having a formal statistics background, it may be hazardous to talk about something that I don’t fully understand. But I can tell you that to the extent that I understand the ecological fallacy, the idea that it applies to individual runs created estimates is hokum.

According to this link, the ecological fallacy occurs when “making an unsupported generalization from group data to individual behavior”. They then use an example of voting. One community has 25% who make over $100K a year, and 25% who vote Republican. Another has 75% who make over $100K and 75% who vote Republican. To use this data to conclude that there is a perfect correlation between individuals voting Republican and making over $100K would be the ecological fallacy. In fact, they show how the data could be distributed so that the correlation between individuals voting Republican and making over $100K is actually negative.

People will then go on to claim that since Runs Created methods are tested on teams, it is wrong to apply them to individuals and assume accuracy. It is true that multiplicative methods like Runs Created and Base Runs make assumptions about how runs are created that are true when applied to teams but cannot be applied to individuals(the well-documented problem of driving yourself in; Barry Bonds’ high on base factor interacts with his high advancement factor in RC, but in reality interacts with the production of his teammates). It is also true that regression equations have many potential pitfalls when applied to teams, let alone taking team regressions and applying them to individuals. However, these limitations are well known by most sabermetricians (although some stubbornly continue to use James’ RC for individual hitters).

The ecological fallacy claim, though, is extended by some to every run estimator that is verified against team data. The claim is that there “need not be little to no connection between team-level functions and player-level functions”. I also saw a critic point out once that run estimators did not do a good job of predicting individual runs scored.

My retort was that the low temperature today in Mozambique did not do a good job of predicting individual runs scored either. To assume that the team runs scored function and the individual runs scored function are the same is to be ignorant of the facts of baseball. A walk and a single have an equal run-scoring value for an individual, and a home run will always have an individual run-scoring value of 1. This is not true for a team, because, except in the case of the home run, it takes another player to come along and drive his teammate in. In the team case, all of these individuals stats are aggregated. The home run by one batter not only scores him, it scores any teammates on base. And therefore the act of scoring runs, for a team, incorporates advancement value as well. A single will create more runs, in average circumstances, then will a walk.

Therefore, when we have a formula that estimates runs scored for a team, it does not estimate the same function as runs scored for a player. It instead approximates another function that we choose to call “runs created” or “runs produced” or what have you. Now it could be claimed, I suppose, that the runs created function cannot be applied to individuals? But why not? If a double creates .8 runs for a team, and a hitter hits a double, why can’t we credit him with creating .8 of the team’s runs? All we are doing is assigning what we know are properly generated coefficients for the team to the player who actually delivered them. Or you can look at it, in the case of theoretical team RC, that we are isolating the player’s contribution by comparing team runs scored with him to team runs scored without him.

Furthermore, the individual runs created function and the team runs scored function are the same function. They have to be. Who causes the team to score runs, the tooth fairy? In the case of the voting situation which was said to be the ecological fallacy, you are artificially forming groups of people that don’t actually interact with each other. I can vote Republican, and you can vote Republican, but we’re not working together in that. You can vote Democrat and I can still vote Republican; our choices are independent. Then you make this group that voted Republican, and look at the their income, and yes, you can reach misleading conclusions.

The point I’m trying to make is that voting is not a community-level function, and therefore it is wrong to attribute the community level data pattern to individuals. People vote as individuals, not as communities. But scoring runs is a team-level function. People create runs as teams, each contributing. If we use a different voting analogy, that of the electoral college, people cast electoral votes as states. And therefore we can break down how much of the electoral vote of Montana that each citizen was responsible for(one share of however many if they voted for the winning candidate, zero if they did not). And that’s what we are doing by looking at individual runs created.

I think the problem, and I don’t mean this to apply to all statisticians who dabble in sabermetrics, but to some, particularly those who don’t have a strong traditional sabermetric background to go along with their statistical knowledge, is that they tend to take all of the things they know can often happen in statistical practice and apply them to sabermetrics, without seeing whether the conditions are in place. In the same way, they will use statistical methods like regression when they are not necessary. If you are studying phenomenon that you don’t have a good theory on, then regression can be a great tool. But if you are studying a baseball offense, you’re better off constructing a logical expression of the run scoring process like Base Runs or using the base/out table to construct Linear Weights. You don’t need a regression to ascertain the run values of events--baseball offenses are complex, but they are not nearly as complex as many of the other phenomenons in the world.


Explanation of Ecological Fallacy

Ec. Fallacy claim applied to RC

Tripod: Ability v. Value

Since I haven't been producing much in the way of new content, I've decided to re-publish some of the articles I posted on my old Tripod website (see link on the side of the page if interested, or just wait for all of the content to show up here). I don't know how long that platform will exist, so the objective is to move stuff over to this blog to preserve it for myself. It's all old - most of it was written between 2001 - 2005, as when this blog started I switched to posting here. When I first started this blog, I had the crazy notion that the content would flow the other way - that I would convert blogposts into "article" format and move them to Tripod site. This piece may include the only successful such migration in the addendum, which first appeared on this blog. I've since written about most of these topics again here, and I certainly think my later work is better, more correct, etc. than the old stuff. I have not done any editing, so there are typos and "thens" in the places of "thans" and the like. I will be putting "Tripod:" in the tile of these re-posts. There will certainly be some statements that didn't age well - see "literal ability" below for a prime example.

This is a topic that gets brought up all the time, both directly and indirectly, in sabermetric circles. If you are discussing the rankings of players, Park Factors, era adjustments, or clutch hitting, this debate will quickly become an issue. Each definition of what we are trying to measure has certain things that should and shouldn't go with it, and so you need to clearly define what you are looking for before you start arguing about it. All of the different definitions are valid and useful things; but which one you are most interested in depends on your preferences and opinions. I personally am most interested in performance, with ability and value both being things I like to look at as well. Literal value or ability does not interest me at all(actually, literal ability probably doesn't interest many sabermetricians at all, because that's what scouts are for and they can probably do it better than we can, although not objectively). So here are the five definitions that I consider:

Literal Value

In a literal value method, you are looking to find the actual value of the player to his team. This means that if the player gets lucky in clutch situations or is used by his manager in a way that enhances his value beyond that of a player with identical basic stats who works in a less valuable situation(like being a closer v. setup man), you take this into account. Literal value is best measured through calculating the players impact on the Win Expectancy of the team, although Run Expectancy methods can also fall under this category. Examples of literal value stats include the Mills brothers' Player Win Average and Tom Ruane's Value Added Batting Runs.

Value

A value method uses conventional statistics, but attempts to do a similar thing with those as the literal value method did-determine how much the player has actually contributed to his team in terms of winning. The basic difference is the lack of a play by play database. It is impossible to implement a literal value system for, say, 1934 because the data that is required just doesn't exist. But in this category, if you have data like batting with runners in scoring position, you can include this. Or considering saves instead of just innings and runs allowed. Many value stats will try to reconcile the individual contributions with those of the team. Some examples of value stats are Bill James' Win Shares and Linear Weights modified for the men on base situations as Tango Tiger does.

Performance

Performance is the category that I am most interested in. In a performance method, you try to ascertain the players performance, based on his basic stats and with no consideration for what game situation they occurred under. A home run in a 15-2 game is just as valuable as a home run in a 2-2 game. A solo home run is equal in value to a game-winning grand slam. This is clearly wrong if you want to determine the players actual value, but many sabermetricians believe that clutch hitting effects are luck, so the method will correlate better from year to year if you look at all events equally. An appropriate Park Factor to couple with a performance measure is a run based park factor, although the line between performance and ability is somewhat blurred, so you could also use a specific event park factor. Some examples of performance measures are Pete Palmer's Total Player Rating, Keith Woolner's VORP, and Jim Furtado's Extrapolated Wins.

Ability

An ability method attempts to remove the player from his actual context completely and put him on an average team. The only proper park factors for an ability method are those that deal with each event separately, since a player can be hurt by playing in a park that doesn't fit his skills, like Juan Pierre with the Rockies. Here, you account for that. Other than that, an ability method will wind up being very similar to performance measures. I can't think of a pure ability method that is commonly used.

Literal Ability

Tango Tiger has called this skill, and that is a good description as well. Literal ability is not really quantifiable in sabermetrics. You can attempt to find a players' literal ability in a certain area of his game, like using Speed Score or Isolated Power. But a players total literal ability is hard to put your finger on. This is what scouts measure-they don't pay attention to the actual results the players put up, but rather how they look while doing it. Actually, if you wanted to do a sabermetric measure for literal ability, there are a host of other factors to consider. For example, I write about the silliness of adjusting for whether a player is right or left handed. This is all assuming you are measuring something other than literal ability. In a literal ability sense, a right handed hitter could be better than a left handed hitter in terms of their pure skills like speed and power, but be less valuable on the field because of the dynamics of the game.

If we can all decide which of the five we are interested in measuring, a lot of silly arguments can be prevented. People frequently criticize the Park Factors in Total Baseball because they are uniformly applied to all players, regardless of whether they hit lefty or righty or whether they have power or not. In terms of literal value, value, or performance, this is a proper decision. But if you want to measure ability, it is an incorrect Park Factor to use.

Additional Thoughts(added 12/05)

In the above article, I defined two classes of value, "Literal Value" and the regular "Value". Literal value, as I define it, involves only methods that track actual changes in run and win expectancy, like Value-Added Batting Runs or Win Probability Added. Value includes methods which use composite season statistics, but give credit for things like hitting with runners in scoring position or a pitcher who pitches in a lot of high leverage situation.

I also broke down ability into "Ability" and "Literal Ability". Ability is defined as "theoretical value", i.e. the value that a player would be expected to accumulate, on average, if he played in a given set of circumstances. Usually this would be our expectation for a player in a neutral park, but it could be "ability to help the team win games in Coors Field" or "in 1915" or "batting fifth in a lineup with A, B, C, and D hitting ahead of him and E, F, G, and H hitting behind him". There are all sorts of different ways you could define ability, but the mathematical result you get will be specific for the context you choose.

Literal ability goes even further, and attempts to distill the player's skill in a given area of the game (such as power, or speed, or drawing walks), or his "overall ability". This is very tricky, because nothing happens in a vacuum, everything happens in some sort of context, and so divorcing a metric from context is pretty much impossible. Therefore literal ability is more of a theoretical concept and not a measurable quantity (although methods like Speed Score are an attempt to measure literal ability in speed, but of course are acknowledged by their creators as approximations).

Anyway, to generalize, value is backwards-looking, and ability is forwards-looking (or at least what might have happened in a different context given the same production in a given timeframe).

The recent signing of BJ Ryan to a large contract by the Blue Jays has put the issue of when to time the value measurement into my head. Literal value methods like Win Probability Added value on a real-time basis. If at a given moment the probability of winning is 60%, and after the next play it increases to 62%, then the player responsible for that play is said to have added .02 wins. So a closer, who pitches as the highest leverage time, will come out with a higher WPA then a starter who had the same performance in the same number of innings.

But if we are ascertaining value after the fact, why do we have to do it in real time? Suppose that Scott Shields is called in to pitch on the road in the bottom of the seventh inning with a one-run lead. According to Tango Tiger's WE chart, the win probability is .647. He retires the side and at the end of the inning, the probability is .732, so he is +.085. He starts the eighth inning with a probability of .704, retires the side, and leaves with a probability of .842, so he is +.138 for the inning and +.223 for the game. In the bottom of the ninth, it is still a one-run game and Francisco Rodriguez is summoned with a win probability of .806. He finishes it off and of course the win probability is then 1, so he is +.194 wins. So Shields, for two innings of scoreless work, only gets .029 more wins then Rodriguez did in one inning. Is this fair? Sure, if you define value real-time. Rodriguez pitched in a more critical situation and his performance did more to increase the real-time win probability.

But since we are looking backwards, why can't we step back and, now, omniscient about what happened in the game, ascertain what value the events actually had? Each out in the game had a win value of 1/27, and since neither allowed any runs or anything else, we don't have to consider that. So Shields should have added 6/27 wins and Rodriguez 3/27. Viewed from the post-game perspective, Shields performance is much more valuable then Rodriguez'. Now you could also argue that if you took this perspective far enough, any event that didn't lead to a run in the end(like a hit that does not score) has no value. And that's a possible outcome of this school of thought.

Now the point is not that real-time value determinations are incorrect or invalid. They are simply a different way of defining literal value. But I would contend that they are not the only way to define literal value. It is one of the easiest to explain and define, and it certainly makes sense. I'm not arguing against it, just arguing that it is not an undeniable choice for what I have called "literal value". Of course, you can define "value" or "literal value" reasonably, in such a way as to make it an obvious choice.

Run Distribution and W%, 2019

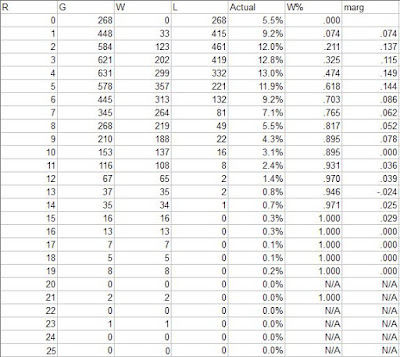
In 2019, the major league average was 4.83 runs/game. It was distributed thusly:



The “marg” column shows the marginal W% for each additional run scored. The mode of runs scored was four, and the fourth run was also the most valuable marginal run; 4.83 is a fairly high scoring environment and not surprisingly these are both higer than the comparable figures from recent seasons.

The Enby distribution (shown below for 4.85 R/G) did its usual decent job of estimating that distribution given the average; underestimating shutouts and one run games while underestimating the frequency of games with two to four runs scored is par for the course, but I dare say it’s still a respectable model:





One way that you can use Enby to examine team performance is to use the team’s actual runs scored/allowed distributions in conjunction with Enby to come up with an offensive or defensive winning percentage. The notion of an offensive winning percentage was first proposed by Bill James as an offensive rate stat that incorporated the win value of runs. An offensive winning percentage is just the estimated winning percentage for an entity based on their runs scored and assuming a league average number of runs allowed. While later sabermetricians have rejected restating individual offensive performance as if the player were his own team, the concept is still sound for evaluating team offense (or, flipping the perspective, team defense).

In 1986, James sketched out how one could use data regarding the percentage of the time that a team wins when scoring X runs to develop an offensive W% for a team using their run distribution rather than average runs scored as used in his standard OW%. I’ve been applying that concept since I’ve written this annual post, and last year was finally able to implement an Enby-based version. I will point you here if you are interested in the details of how this is calculated, but there are two main advantages to using Enby rather than the empirical distribution:

1. While Enby may not perfectly match how runs are distributed in the majors, it sidesteps sample size issues and data oddities that are inherent when using empirical data. Use just one year of data and you will see things like teams that score ten runs winning less frequently than teams that score nine. Use multiple years to try to smooth it out and you will no longer be centered at the scoring level for the season you’re examining.

2. There’s no way to park adjust unless you use a theoretical distribution. These are now park-adjusted by using a different assumed distribution of runs allowed given a league-average RA/G for each team based on their park factor (when calculating OW%; for DW%, the adjustment is to the league-average R/G).

I call these measures Game OW% and Game DW% (gOW% and gDW%). One thing to note about the way I did this, with park factors applied on a team-by-team basis and rounding park-adjusted R/G or RA/G to the nearest .05 to use the table of Enby parameters that I’ve calculated, is that the league averages don’t balance to .500 as they should in theory. The average gOW% is .489 and the average gDW% is .510.

For most teams, gOW% and OW% are very similar. Teams whose gOW% is higher than OW% distributed their runs more efficiently (at least to the extent that the methodology captures reality); the reverse is true for teams with gOW% lower than OW%. The teams that had differences of +/- 3 wins between the two metrics were (all of these are the g-type less the regular estimate, with the teams in descending order of absolute value of the difference):

Positive: None
Negative: HOU, OAK, LA

I used to show +/- 2, but with the league gOW% being .490, there’s nothing abnormal about a two win difference (at least on the negative side). Were I more concerned with analysis rather than the concept, I would take some stronger efforts to clean up this issue with more precise application of park factors and Enby coefficients, but I consider this post to be more of an annual demonstration of concept.

Teams with differences of +/- 3 defensive wins were:

Positive: PIT, MIL, SEA, BAL
Negative: None

I usually run a graph showing the actual v. Enby run distribution of the team with the biggest gap on offense or defense, which was Houston’s offense. However, I don’t find their situation particularly compelling, as they had a handful of games with a lot of runs scored, which is easy to understand. More interesting is Pittsburgh, whose defensive run distribution produced a .445 gDW% but only a .416 DW% (the graph shows the Enby probabilities for a team that allowed 5.6 R/G using c = .852, which is used to calculate the gOW%/gDW% estimates):



Even as someone who has looked at a lot of these, it's hard to articulate why this was a good thing for Pittsburgh (good in the sense that their runs allowed distribution should have resulted in more wins than a typical runs allowed distribution for a team allowing 5.6 per game). The Pirates had slightly more shutouts and one run allowed games than you’d expect given their overall RA/G, but the they had many more two run games, which are games that a team with an average offensive in a 4.75 R/G environment (which is the league average after adjusting for the PIT park factor) should have won 82.0% of the time. They gave some of this advantage back by giving up three runs more often (still a good amount to allow with a .686 W%), but they also had more four run games (still a .543 W%). They allowed 5-9 runs less often then expected, and those are games that they would be expected to lose (especially 6+, as the expected W% drops from .409 when allowing five to .296 when allowin six).

I don’t have a good clean process for combining gOW% and gDW% into an overall gEW%; instead I use Pythagenpat math to convert the gOW% and gDW% into equivalent runs and runs allowed and calculate an EW% from those. This can be compared to EW% figured using Pythagenpat with the average runs scored and allowed for a similar comparison of teams with positive and negative differences between the two approaches:

Positive: MIL, BAL
Negative: OAK, BOS, LA

The table below has the various winning percentages for each team: