On Run Distributions, pt. 2: Negative Binomial

There does exist a common discrete distribution that can be useful in modeling the per game run distribution. It doesn’t necessarily seem like it should work, since the questions that the distribution is typically employed to answer (at least in the sort of non-expert presentations most people are exposed to) doesn’t have an obvious connection with expected runs scored in baseball. Is it a perfect fit? Of course not; there are no perfect models anyway, but even granting that, it has flaws. Would it work in extreme circumstances? I don’t really know; over the next several articles I’ll take a stab at answering these questions, but obviously I have my limits as an analyst.

I did a couple of internet searches to try to see if there were any published papers or articles using the Negative Binomial distribution to model runs scored. There were a few that seemed to mention it, and there was an article about cricket scoring, but I didn’t see anything using it for the exact purpose I am. That does not mean none exist.

In any event, I know that I am not the first person to use the distribution to model runs per game, because I was sent an unpublished paper about it several years ago by Phil Melita. Melita sent it to me since he had cited Pythagenpat in the article, and we traded a couple emails about it. It was never published in By the Numbers, though, and I’m not sure why. In any event, Melita didn’t present his work in the same manner that I am here, but it was clearly along the same lines and I can take no credit for any originality here. I hadn’t thought about it in a few years, but as soon as I tried the negative binomial, I remembered Melita’s article.

To be honest, the negative binomial is not one of my favorite distributions. From my educational experiences, it is associated with two things in my mind: 1) the nice, simple Geometric distribution (a special case of negative binomial) run amuck and 2) Poisson-Gamma compound processes. It does have other obvious baseball uses, but it’s just not as intuitive to me as Poisson, Geometric, or Binomial.

The way the negative binomial distribution is usually presented masks its ability to deal with fractional parameters, hidden by the use of factorials and the aversion of everyone but mathematicians to gamma functions. And the problems to which the negative binomial is usually applied are along the lines of “What is the probability of 5 successes before the eighth failure?”, which further reduces the likelihood that people will consider it as a model for run scoring. However, the pmf for the negative binomial can be written thusly:

p(k) = (1 + B)^(-r) for k = 0
p(k) = (r)(r + 1)(r + 2)(r + 3)…(r + k - 1)*B^k/(k!*(1 + B)^(r + k)) for k >=1

where r and B are the parameters of the distribution and k is the point at which we are calculating the probability.

Of course, in order to actually use this or any other distribution, we need to be able to define the parameters. Everything that follows in this series of posts needs to be prefaced by this caveat--I am not a statistician or a probability expert. Compared to the average person, I have a lot of knowledge through my own curiosity and my studies/profession. Compared to the average person who dabbles in sabermetrics, though, my knowledge doesn’t stand out, and obviously I am a kindergartner compared to the experts in these fields.

So here I will take the easy step of fitting the parameters of this distribution using the method of moments. There may well be a better, more precise method out there (maximum likelihood estimation always comes to mind, but is a nightmare for negative binomial). In any event, the most important simple properties of any distribution are its mean and variance. For negative binomial, these are computed as follows:

mean (u) = r*B
variance(v) = r*B*(1 + B)

The method of moments uses the first two central moments (mean and variance to estimate the parameters). If we take the ratio of v to u, we can estimate B:

v/u = r*B*(1 + B)/(r*B) = 1 + B
Ergo B =v/u - 1 and r = u/B = u^2/(v - u).

For 1981-96, the average runs scored per game was 4.4558 with a variance of 9.3603, which leads to an estimate that B = 9.3603/4.4558 - 1 = 1.1007 and r = 4.4558/1.1007 = 4.0480.

Given those parameters, here are the estimates for the first few run totals:

p(0 runs) = (1 + B)^(-r) = (1 + 1.1007)^(-4.048) = .0496
p(1 run) = r*B^k/(k!*(1 + B)^(r + k)) = 4.048*1.1007/(1!*(1 + 1.1007)^(4.408 + 1)) = .1051
p(2 runs) = r*(r + 1)*B^k/(k!*(1 + B)^(r + k)) = 4.408*(4.408 + 1)*1.1007^2/(2!*(1 + 1.1007)^(4.408 + 2)) = .1390
p(3 runs) = r*(r + 1)*(r + 2)*B^k/(k!*(1 + B)^(r + k)) = 4.408*(4.408 + 1)*(4.408 + 2)*1.1007^3/(3!*(1 + 1.1007)^(4.408 + 3)) = .1468

The r*(r + 1)*(r + 2)*(r + 3)*(r + 4)*... formula gets annoying, but with a spreadsheet it is easy to implement. Here is the complete runout (to 16 runs), along with a graph comparing the estimate probabilities to the observed frequencies:





When I look at that graph, I see a pretty decent fit, one that makes me believe that the negative binomial distribution may have some usefulness in estimating run distributions. Is it perfect? No; as you can see, it is noticeably low on shutouts (an issue that I will go into detail about in the next post), and it’s too high for some of the other common scores (2-4). Using the X^2 test statistic described in the previous post, this scores a 176, which is easily better than the other crude models I considered.

Of course, I’ve only dealt with scoring at normal levels. In order to estimate run distributions for other scoring levels, we’ll have to change the parameters. The mean number of runs per game is always known, but the variance is a quantity that we can only know if we have prior knowledge of the empirical run distribution. Since both r and B are dependent on both the mean and variance, they will be constantly changing when the mean and variance of the distribution we are fitting to changes.

Before worrying about how to tackle that problem, we first need to make sure it would be worth attempting to adapt to non-average situations. I will consider the top and bottom 5% of teams by R/G for the data in Davenport’s spreadsheet--the 25 lowest and highest scoring teams of 1981-2006. The bottom 25 teams averaged 3.49 R/G with a variance of 6.6206, which produces estimates of B = .897 and r = 3.891. The results:



This doesn’t look as nice, but it still appears as if the model does a decent job. Remember that the sample size is not that large (25 teams is a smaller sample than a full major league season), so there’s the possibility of some random fluctuation. Again, the point here is not to perform a rigorous test, but rather to make sure the model isn’t completely out in left field.

The 25 highest scoring teams averaged 5.7 R/G with a variance of 12.4 for B = 1.175 and r = 4.849:



Not bad. Next time, I’ll discuss a workaround for the underestimation at zero runs (albeit one that introduces a new stumbling block).

On Run Distributions, pt.1: Introduction

Let’s suppose that you were going to conjure up a model that fit the distribution of team runs per game. What properties would you like it to exhibit (ignoring for the moment whether a model with such properties is actually feasible)?

I would suggest the following:

1. It should be discrete. Runs scored in a game is a discrete quantity. There’s no such thing as a fractional number of runs scored. There’s nothing wrong with suggesting that a certain combination of events will generally create, say, 4.35 runs, but that 4.35 runs represents a weighted average of all the times that combination produces 0, 1, 2, 3, 4, 5, …, runs. The distribution function should reflect those probabilities.

2. It should be a standard, well-known probability distribution.

3. It should be accurate, and adaptable across a wide range of scoring contexts. This is the most important, but also should go without saying.

4. If possible, it should be simple. I am not suggesting trading accuracy or theoretical purity for simplicity, but this is a wish list.

Again, that is a wish list. In the real world, you have to model reality. That might mean accepting a continuous distribution as a model of a discrete function, or having a method that is useful in normal contexts but has some structural deficiencies that limits its utility at the extremes.

If we want to find a distribution that meets some of the criteria on the list, we have to start with discrete distributions. I would assume that the first such distribution that comes to mind for most people with any background in probability or statistics is the Poisson distribution. The Poisson distribution is simple, adaptable, and has a cool name and a cool Greek letter for a parameter. Unfortunately, it doesn’t work as a model of runs scored in baseball, despite some noble efforts to make it so.

Poisson does work fairly well (at least to the extent of my knowledge, which is limited) as a model of soccer and hockey scoring. Given that it is often used for situations in which events are expected to occur over a certain period of time (or area and other physical intervals), it makes intuitive sense that it wouldn’t fit baseball run scoring, since time is not a factor. A Poisson process should be able to be extended to time periods other than the basis--that is, if your mean is 3 goals per game for hockey, you should be able to use the distribution to estimate goals per period (with mean 1) or goals per ten games (with mean 30), or goals per 3714 games (with mean 11142).

This property obviously does not carry over to baseball due to the nature of the game. One could picture it working for converting between innings and games, but once you get to the inning level and start splitting into outs, the pattern of runs scored is not the same independent of the number of outs in the inning (i.e. more runs are scored with two out than zero out).

As you can see in the chart in the Clay Davenport article I linked above, the Poisson distribution severely underestimates the proportion of shutouts. This is an issue that can be sidestepped by using a modified value at zero, but the slope at non-zero runs is not close enough to reality to salvage a Poisson approach, and the relationship of the mean of runs scored in relation to the variance is not a match for Poisson.

In lieu of a simple distribution, those examining baseball scoring have had to be creative. The three-parameter Weibull distribution (a continuous distribution) has been used with good results by Dr. Steven Miller and Sal Baxamusa to model runs scored. The Tango Distribution, which models runs scored per inning, can be used to estimate the per game distribution with the use of some combination math published by Ben Vollmayr-Lee (zip link) (as an aside, one of the topics in statistics that confuses me the most is combinations and permutations. Sure, I understand why 9! gives you the number of possible batting orders for nine players, and I understand the binomial coefficient, but start asking more detailed questions about pulling colored balls out of urns with and without replacement and I started to wish that I was studying liberal arts.)

With the recent publication of Bill James’ old Baseball Analyst newsletters, I was able to read Dallas Adams’ article in the June 1982 issue in which he uses the following functions to estimate scoring distribution as a function of R/G:

When N is 5 runs or fewer: P(N) = A + B*N + C^2*N

where A = .38498 - .10839 (R/G) + .0080055(R/G)^2
B = .0010306 + .024139 (R/G) - .002943(R/G)^2
C = -.01879 + .002514(R/G) - .00001506(R/G)^2

When N is 6 runs or more: P(N) = D(E^N)
where D = 6.6210 - 2.4965(R/G) + .27518(R/G)^2
E = .058479 + .24022(R/G) - .022291(R/G)^2

That’s the kind of thing I’d like to avoid if at all possible, no offense to Mr. Adams and the others who have made the effort to work on this problem.

Let me close out this post by offering a quick look at the Adams formula and the failures of Poisson, while introducing a set of data that I’ll use to fit a model in the next installment. I have a spreadsheet (I believe it was put together by Clay Davenport or Keith Woolner, but I can’t find the original link) with the runs per game for each major league team 1981-96. The aggregate distribution for these teams was:



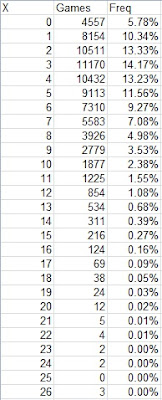
The easiest way to fit a Poisson model to this data is to use the maximum likelihood estimate that the parameter h is equal to the sample mean (this is also equivalent to the method of moments estimate in this case). In this case the mean R/G is 4.456 and the variance is 9.36 (those of you familiar with Poisson can already see this is not going to end well as a Poisson distribution has a mean equal to its variance).

The probability mass function for Poisson is:
P(x) = e^(-h)*h^x/x!

For example, the estimated probability of scoring 3 runs is e^(-4.456)*4.456^3/3! = .1712. The empirical probability in this case is ,1417, and this is one of the more accurate points:




As you can see, the Poisson model bunches too much probability around the mean, leaving estimates of high scoring games too low and estimates of low scoring games way too low.

I will also look at Adams’ formula just for kicks. The constants for 4.456 R/G are A = .0610, B = .0502, C = -.0079, D = .9606, E = .6863, yielding these estimated probabilities:




Adams better matches the actual distribution for normal amounts of runs scored, but overestimates the likelihood of extremely high run output. Since he uses formulas that don’t tie to a true probability distribution which adheres to the requirements thereof (most importantly that the sum of all probabilities is one), the estimated probabilities total to 1.03 and runs per game to 4.61.

My point is not to pick on a thirty-year old formula from a pioneering sabermetrician--the fact that luminaries such as Adams and Davenport have not been able to come up with a satisfying approach to this problem serves to illustrate its difficulty, and hopefully to cause you not to judge too harshly the method that I offer in the next post as flawed but useful in certain circumstances.

Before closing this post, let me provide a crude measure of the relative accuracy of the models. Basically, it is the chi-square test statistic. For each number of runs scored (0, 1, 2, etc.), calculate (Expected games with n runs - actual games with n runs)/Expected^2. Here, I will group all games of 15+ runs together, which could be a problem if we encounter a distribution that overpredicts extremely high scores.

I will be doing this test (which I’ll call X^2) without any of the trappings of an actual chi-square test: degrees of freedom, critical values, and the like. The point is not to perform a real significance test--it's to get a quick idea of how these models stack up against one another. I will at various points in this series be testing the model with the same data that was used to fit its parameters--obviously a no-no if you want an unbiased test. However, the first basic test for a model is whether or not it can describe the data it was fitted with. If it can’t do that, there’s absolutely no point in worrying about how it handle out of sample data. None of the models I’m going to be offering up in this series are clearly good enough to move on to that next step.

So, for the Poisson, Adams, and modified Adams (I rescaled so that the total probability would be equal to one) distributions, here are the X^2 values for the model versus the 1981-96 data:
Poisson 91996
Adams 371
Modified Adams 305

Poisson with no fudging obviously doesn’t match runs scored, but is provided here so that you can see how a truly worthless model fares.

Meanderings

* As sabermetrics has matured, many of us have come to recognize to a greater extent that information asymmetry hinders our analysis of transactions and other team decisions. Teams certainly operate with much greater information about their own players than their opponents do, and much, much greater information than we could have hope to possess as outsiders. This is a positive step for sabermetrics, one that I certainly needed to heed more in my earlier days pretending to be more of a know-it-all than I do now.

However, one can go too far, and use information asymmetry as an excuse for questionable decision-making. For the 2012 MLB season, I would make the Reds usage of Aroldis Chapman Exhibit A. Chapman was groomed throughout the winter and the spring as a starter, and seemed to be handling it well. There was really no reason to believe that he wouldn’t, since he had previously started both in Cuba and in Louisville in 2010. Then the Reds suffered injuries to Nick Masset, Bill Bray, and Ryan Madson, and Chapman was moved to the bullpen.

It’s possible, of course, that the Reds always had grave reservations about utilizing Chapman as a starter, and that the bullpen injuries tipped the scale in a direction it was already beginning to go. But given the timing, it seems very unlikely.

Now the Reds have made a second decision, to use Chapman as the closer, for which there is again no evidence that it was prompted by inside information. Instead, the cause is pretty straightforward--continuing poor performance in that role by Sean Marshall, capped by a game in which he had to be rescued by Jose Arredondo.


* With I’ll Have Another set to make a bid for the Triple Crown, there will be two opposing yet equally silly points of view on display among the lesser lights of sportswriting.

The first is that I’ll Have Another cannot be beaten. They will point out the perceived weak Belmont field that does not include Bodemeister, talk about the horse’s “will to win”, and say that they just can’t imagine how he gets beat. Of course, the fact that similar things were written about Smarty Jones and Big Brown will be completely ignored, as sportswriters of this class are incapable of learning. The obvious fact of the matter that if Northern Dancer, Majestic Prince, Spectacular Bid, Alysheba, and Sunday Silence can all fail to win the Belmont, then any horse could as well (not to mention losses in other races, like Native Dancer and Point Given in the Kentucky Derby) will also be ignored.

The second is that I’ll Have Another can’t win because he is running against 34 years of failure and the ten horses in that period that have won the Derby and the Preakness before losing the Belmont. This is also silly; one need only to look at the margin by which Victory Gallop denied Real Quiet to know that the Triple Crown is winnable, not to mention trying to explain who would have beaten Sunday Silence if not for another all-time great in Easy Goer, and many other similar arguments.

Then there is the matter of what it would mean if I’ll Have Another wins the Belmont. Where would that rank him historically? For those that know nothing about horse racing other than the Triple Crown (which is a large share of the general public), it would obviously put him in an elite group of twelve. For those of us that have a broader knowledge about the sport, it wouldn’t really mean a whole lot for his historical standing. It would certainly make him the most famous American horse of recent memory, but he would have to achieve more in his career to be noted as particularly remarkable.

That is not my attempt to downplay the Triple Crown--there's no professional sports outcome I’d rather see other than the Indians winning the World Series and the Browns winning the Super Bowl. But the Triple Crown is three races run over a month and a half in the middle portion of a horse’s three-year old campaign. It is but a small portion of what makes an all-time great race horse. Many all-time greats didn’t contest the Triple Crown, but went on to achieve great things later in their three-year old seasons (see Buckpasser for an example, or Tiznow in more recent history). Many more were non-factors at three, but achieved great things later in their careers (listing examples here would be silly as there are so many).

Of course, evaluating a horse from a historical perspective must include consideration of context. Today’s thoroughbreds race much shorter schedules and are less likely to return to run at age four and later if they are stars at three. Still, even from the perspective of three-year old stars of the last fifteen years, even a Triple Crown will not raise I’ll Have Another above the very best. Point Given may have lost the Kentucky Derby, but he came back in the summer to win the Travers at the same distance, and ran one of the best Belmonts of recent memory. That his “Triple Crown” runs Preakness-Belmont-Travers doesn’t make it much less of an achievement. Curlin may have lost the Derby and the Belmont, but he came back in the fall to win the Jockey Club Gold Cup and the Breeders’ Cup Classic against the best older horses in the country.

On the other hand, the same can be written about some of the other horses that have won the Triple Crown. It is easy to believe that the eleven Triple Crown winners represent the greatest American thoroughbreds, but it really isn’t the case. Certainly all eleven are well-regarded historically and are in the Hall of Fame, but in a couple of cases, that is mostly the result of winning the Triple Crown and not anything else they did.

- Sir Barton won the Triple Crown before anyone talked about such a thing (that would start with the second winner, Gallant Fox). For his career he won 13 of 31 starts. He was Horse of the Year in 1919, and was ranked by Blood-Horse as the #49 American thoroughbred of the Twentieth Century.

- Omaha was sired by the 1930 Triple Crown winner Gallant Fox, but he wasn’t even named Horse of the Year in 1935. He won 9 of 22 career starts and was ranked #61 by Blood-Horse.

It’s not a knock on I’ll Have Another to say that he’d be more Omaha than Count Fleet should he win the Belmont. And if the horse can stay in training and win the Breeder’s Cup Classic or another key race against older horses, I’d be inclined to change my opinion. But that’s a hard task for a three-year old, and the horses that can do it are the ones that distinguish themselves as the best, Triple Crown or no.

* Speaking of horse racing and circling back to baseball, with the season roughly 25% complete I have heard multiple announcers referring to the “quarter pole”. I find this extremely aggravating (which is admittedly a bit of an overreaction). Unless there is some non-horse racing definition of the term “quarter pole” of which I am unaware, using the term in this manner is completely wrong. The quarter pole does not have anything to do with one quarter of the race--it is the pole marking a quarter mile to the finish line. And as you can see from that description, it is oriented to the end rather than the beginning of the race. There is no use for miles in baseball, so I suppose the most appropriate use of the term would be after 120 or so games had been played--a quarter of the season remaining.

I realize that I am complaining extensively about a very silly thing, but when a term from one of my favorite sports gets twisted by people I am predisposed to complain about anyway, I can’t help myself. Off the top of my head, I can’t think of a similar example of a baseball term used in other contexts that so completely misses the point (which isn’t to say one doesn’t exist). The closest I can come up with is “balanced scorecard”, which has been turned into some sort of silly business jargon, kind of how statisticians must bristle when they hear about “Six Sigma”.

Scoring Self-Indulgence, pt. 9

Finally, it’s over. No more boring you with detailed explanations of a fairly conventional scoring system as if it is unique and deserving of great attention. I will close with a pitch-by-pitch translation of a scoresheet into text. Truly fascinating, I know.

This game was played on July 24, 2010 between Los Angeles and Texas. The lineups were as follows:

Umpires
H--Holbrook
1--Gibson
2--Knight
3--Davis

Los Angeles
1. 6 Aybar
2. 4 Izturis
3. 9 Abreu
4. 8 Hunter
5. D Matsui
6. 5 Callaspo
7. 3 Napoli
8. 2 Mathis
9. 7 Willits
P: Santana

Texas
1. 6 Andrus
2. 5 Young
3. 4 Kinsler
4. D Guerrero
5. 7 Hamilton
6. 9 Cruz
7. 2 Molina
8. 3 Davis
9. 8 Borbon
P: Feldman



LAA First
Aybar: Called strike, foul, ball, ball, ball; flied to left (along line)
Izturis: Called strike, ball, foul, ball, foul; foul to third
Abreu: Ball, called strike; lined to right
0 runs, 0 hits, 0 walks, 0 left on base, 15 pitches

TEX First
Andrus: Ball, called strike, called strike, ball; grounded to first (pitcher covering)
Young: Called strike, called strike, ball; lined to right
Kinsler: Called strike, swinging strike, foul; struck out swinging
0 runs, 0 hits, 0 walks, 0 left on base, 13 pitches

LAA Second
Hunter: Ball, foul, swinging strike, foul, ball; flied to right
Matsui: Lined to right
Callaspo: Ball, called strike, ball, grounded to first (pitcher covering)
0 runs, 0 hits, 0 walks, 0 left on base, 11 pitches (26 for game)

TEX Second
Guerrero: Ball; grounded to short
Hamilton: Ball, ball; grounded to first
Cruz: Flied to center
0 runs, 0 hits, 0 walks, 0 left on base, 6 pitches (19 for game)

LAA Third
Napoli: Called strike; flied to center
Mathis: Called strike, swinging strike, foul, ball; flied to center in center-right
Willits: Called strike; flied to left
0 runs, 0 hits, 0 walks, 0 left on base, 9 pitches (35 for game)

TEX Third
Molina: Called strike, ball, called strike; struck out swinging
Davis: Ball, called strike, ball, ball; doubled to right-center very deep on line drive
Borbon: Ball, called strike, foul, ball, ball; flied to center
Andrus: Ball, called strike, foul, ball; grounded to short
0 runs, 1 hit, 0 walks, 1 left on base, 20 pitches (39 for game)

LAA Fourth
Aybar: Bunt foul; singled to left along line, thrown out stretching to second (left to second)
Izturis: Called strike showing bunt, ball; flied to left
Abreu: Called strike, ball, ball, ball; walk
Hunter: Ball; singled to right on flyball, advanced to second on fielding error by right fielder, Abreu to third
Matsui: Called strike, ball; popped to shortstop in shallow left
0 runs, 2 hits, 1 walk, 2 left on base, 15 pitches (50 for game)

TEX Fourth
Young: Grounded to second
Kinsler: Ball, ball, called strike, ball; walk
Guerrero: Grounded into double play, third to second to first, Kinsler retired at second
0 runs, 0 hits, 1 walk, 0 left on base, 7 pitches (46 for game)

LAA Fifth
Callaspo: Ball; grounded to pitcher
Napoli: Ball, called strike, foul, ball; grounded to third
Mathis: Called strike showing bunt, ball, ball, ball; homered to left on flyball, RBI
Willits: Called strike; singled to right on flyball
Aybar: Ball, ball; tripled to right along line on line drive, Willits scored, RBI
Izturis: Ball, foul, foul; flied to right in right-center
2 runs, 3 hits, 0 walks, 1 left on base, 21 pitches (71 for game)

TEX Fifth
Hamilton: Foul; flied to center
Cruz: Foul, swinging strike, ball; struck out swinging
Molina: Foul; singled to center on groundball
Davis: Called strike, foul; struck out swinging
0 runs, 1 hit, 0 walks, 1 left on base, 11 pitches (57 for game)

LAA Sixth
Abreu: Grounded to second
Hunter: Foul, ball, singled to center on groundball
Matusi: Ball, Ball, called strike, foul; singled to right-center, Hunter to third
Ogando relieved Feldman (9 pitches in inning, 80 for game)
Callaspo: Called strike, singled to shallow center on flyball, Hunter scored, Matsui to second, RBI
Napoli: Swinging strike, ball, swinging strike, foul, ball, ball, foul, foul, foul, foul, foul; struck out looking
Mathis: Ball, swinging strike, foul; grounded into fielder’s choice at third, Callaspo retired at second (third to second)
1 run, 3 hits, 0 walks, 2 left on base

TEX Sixth
Borbon: Ball, called strike showing bunt, swinging strike, ball; struck out swinging
Andrus: Ball, ball; flied to right along line
Young: Called strike, ball, ball; homered to left-center on flyball, RBI
Kinsler: Ball, swinging strike, foul, ball, ball; walk
Guerrero: Ball (Young stole second); grounded to third
1 run, 1 hit, 1 walk, 1 left on base, 20 pitches (77 for game)

LAA Seventh
Oliver relieved Ogando
Willits: Ball, called strike, ball; singled to center on flyball
Aybar: Bunt foul, bunt foul; singled to right on groundball, Willits to third
Izturis: Called strike, ball; singled to right on groundball, Willits scored, Aybar to second, RBI
Abreu: Bunt foul; doubled down the right field line on a groundball, Aybar scored, Izturis to third, RBI
Hunter: Intentional ball, intentional ball, intentional ball; intentional walk
Matsui: Foul, ball; grounded into fielder’s choice at first, Izturis retired at home (first to catcher), Abreu to third, Hunter to second
Callaspo: Foul, ball, called strike; flied to center in center-right, Abreu scored, sacrifice fly, RBI
O’Day relieved Ogando
Napoli: Ball, ball, ball, called strike; grounded into fielder’s choice at shortstop, Matsui retired at second (shortstop to second)
3 runs, 4 hits, 1 walk, 2 left on base

TEX Seventh
Hamilton: Flied to center in deep center-left
Cruz: Ball, called strike; homered to left on flyball, RBI
Molina: Flied to deep right
Borbon: Ball, called strike, swinging strike; struck out swinging
1 run, 1 hit, 0 walks, 0 left on base, 9 pitches (86 for game)

LAA Eighth
Harrison relieved O’Day
Mathis: Ball, called strike; singled to left on flyball
Willits: Foul bunt; bunted into fielder’s choice at catcher, Mathis retired at second (catcher to shortstop)
Aybar: Swinging strike, ball, ball, swinging strike (Willits caught stealing catcher to second), ball, foul; walk
Izturis: Ball, called strike; popped to second in shallow right
0 runs, 1 hit, 1 walk, 1 left on base

TEX Eighth
Borbon: Called strike; singled to shallow left along line on flyball
Andrus: Ball, called strike, called strike, foul; struck out swinging
Young: Ball, ball, called strike, ball, called strike, foul; struck out looking
Kinsler: Called strike, swinging strike; popped to first
0 runs, 1 hit, 0 walk, 1 left on base, 17 pitches (103 for game)

LAA Ninth
Mathis relieved Harrison
Abreu: Ball, ball, called strike, ball; walk
Hunter: Ball; reached on fielding error by second baseman, Abreu to second
Matsui: Ball, foul, ball, ball; grounded to second, Abreu to third, Hunter to second
Callaspo: Popped to short
Napoli: Ball, ball, ball, called strike, foul, foul; looped to second
0 runs, 0 hits, 1 walk, 2 left on base

TEX Ninth
Rodney relieved Santana
Guerrero: Ball, ball, ball, called strike, called strike; struck out looking
Hamilton: Ball, called strike, swinging strike, foul, ball; doubled to center-right on flyball
Cruz: Called strike, foul, foul, ball, ball; struck out swinging
Molina: Called strike, foul, ball, ball, ball, foul, foul; struck out looking
0 runs, 1 hit, 0 walks, 1 left on base
LAA 6, TEX 2

Great Moments in Yahoo! Box Scores

This is from the same game I posted earlier.  Yahoo! has corrected the score, but remain confused with respect to the participants in the game.

Great Moments in Yahoo! Box Scores

The score was 12-1.

Great Moments in Yahoo! Box Scores

Scoring Self-Indulgence, pt. 8: Substitutions and Miscellany

I’ve covered most of the on-field events that I record on my scoresheet; the only major area of keeping a scoresheet remaining is how to record substitutions.

Focusing first on position players, the four types of substitution/switches that can occur are:
1. pinch-hitting
2. pinch-running
3. defensive replacement
4. defensive position switch

The first principle of my system for tracking these is that all substitutions are assumed to occur at the start of the inning unless otherwise noted, except for pinch-runners. They are assumed to enter the game as soon as the player they replace reached base unless otherwise noted. If a player enters the game while his team is batting, he is assumed to be a pinch-hitter unless otherwise noted.

The point at which the substitute enters the game is noted pretty simply, by writing his name below the starter’s name in the appropriate box followed by a notation like “v7” (bottom of the seventh) or “^4” (top of the fourth). In the past, I would have rendered those as “B7” and “T4” respectively, but I started using carrots a couple years ago when I moved to have less letters and more symbols on my sheets. Either way, the meaning is easy to decipher.

If the replacement is a pinch-runner (and he comes into the game as soon as the original player reached base), then the prefix “PR” is used; “PR Jones ^8” means, obviously, that Jones pinch-ran in
the top of the eighth.

For defensive replacements, there is no position recorded for the new player if it is the same as the old one. If the starter was “6 Peralta” (that is, shortstop Peralta) and he is replaced by defensive replacement McDonald in the bottom of the seventh, I’d simply write “McDonald v7”. If the replacement is at a different position than the man he replaced, then the position is written in front, i.e. “4 McDonald v7” if McDonald is playing second base.

With respect to defensive position switches, suppose that Gerut begins the game in center field and then moves to left in the top of the sixth. The initial lineup would read “8 Gerut” of course; the switch will be noted by simply writing “7 ^6” wherever it will fit, preferably next to the original position/name but if not then on the next line below.

Mid-inning switches are fairly straightforward, although a little trickier. For pinch runners, suppose that in the top of the ninth, the #4 batter reaches base, then moves to third on the actions of the #5 hitter, and then is removed for a pinch-runner as the #6 batter comes to the plate. The notation I would use is “PR Jones 6-9”. In this case, 6 is the lineup slot at the plate at the time the substitution is made and 9 indicates the inning. It is not necessary to indicate whether it is the top or bottom of the inning, as the pinch-runner notation makes it clear that it must be his team’s batting half. Of course, this applies to the original PR notation as well, for which I do note the inning-half, but I drop that detail here because the extra number and dash will already be cluttering things up.

The use of the “lineup slot-inning” format may seem a little backwards since the inning is the more important distinguishing factor of when the substitution takes place, but it is derived from the orientation of the scoresheet and considering it as I would a spreadsheet. The lineup slots represent the rows down the vertical of the page, while the innings represent the columns along the horizontal. It is natural for me to put the vertical first, I guess.

For a mid-inning defensive replacement, it is necessary to record the half of the inning, because otherwise it could be confused with a pinch-hitter. For example, if Branson comes in to play third in the bottom of the third with the #8 hitter at the plate, directly replacing the previous third baseman in the batting order, I’d writer “Branson 8v3”.
The exception would come if the substitute went into a different lineup slot, replacing a player at a different position. In that case, I could just write “5 Branson 8-3”, with the notation of the new position demonstrating that this is a defensive replacement and not a pinch-hitting situation. The same rule applies to any defensive pitching switches.

If a substitution occurs between pitches of a plate appearance, then a little more finesse is required. The notation takes the form “Ax”, where x is the last pitch thrown before the substitution is made. If there is a pinch-hitter after the second pitch to the #8 batter in the top of the ninth, the replacement could be recorded as “Harris 8v9 (AB)”. Similar notation is used for pinch-runners and defensive replacements; again, it’s unnecessary to record which half of the inning it is for pinch-runners or defensive position switches.

If a player is ejected, I write “EJ 3^7” or something similar; this would indicate that the player was ejected, with the first PA he was not eligible for being that of the #3 hitter in the top of the seventh. If he was ejected at the end of an inning/between innings, the notation could just be “EJ v7”.

Pitcher substitutions are recorded in the box for pitchers similarly to how position player substitutions are recorded. The exception is that a pitcher brought on to start an inning is noted simply with the inning number; there’s no need to distinguish between top and bottom. Any changes in the batting order status of the pitcher are recorded in the appropriate box, not in the pitcher section of the scoresheet.

So if Huff starts the game, is relieved by Sipp to start the seventh, then by Herrmann to face the #8 batter in the seventh, the pitchers box would read: “Huff, Sipp 7, Herrmann 8-7”.

If the game goes into extra innings and I have to move onto another scoresheet, I recopy the lineup as it is when the game goes to extra innings. This can include some odd-looking notations, like players at positions they don’t actually play if they pinch-hit or pinch-ran, but doing it this way allows for one to see that the defense was reshuffled at that point. That way the change that occurs for the tenth inning can be marked on the new extra-inning scoresheet rather than on the sheet used for innings 1-9. If the pitcher that finished the ninth stays in for the tenth, I put his name in brackets just to avoid any confusion with the starting pitcher, who is also not listed with any entry point (ex. [Wilson]).

Some other assorted miscellany in no particular order:

* If a team bats around, I just move over to the next column. From then on, instead of using the lineup slot to refer the reader of the sheet back to the appropriate scorebox, I add an “A” at the end. So if a team bats around and the tenth batter is the #7 hitter, his box is now referred to as “7A”. If for some reason the inning keeps going, the scorebox for his third PA of the inning would be “7B”.

* If a batter’s PA ends prematurely due to an out on base or the end of the game (with a run scoring on a not in-play event), I write “IE” for inning ended across the box, and make the inning ending slash so that it will be clear that the next inning beings with his PA:



* At the end of each inning I record a basic line score for the inning in the inning header. This takes the form R-H-W-LOB. Above it, I record the number of pitches thrown in the inning by the starting pitcher and his running pitch count for the game. When he exits, I stop recording pitch counts. So, if a team scores a run on a hit with no walks and no one left on in the second inning, with the pitcher making 17 pitches after making 8 in the first inning, the inning header would look like this:



When the pitcher is finished, the last updated cumulative pitch count is indicated by a dash between the final inning pitch count and the game total.