Career WAT Data, 1946-1960

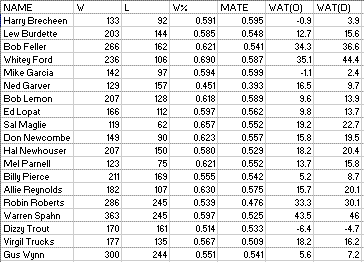
Actual W-L along with Oliver and Deane WAT:



I bet if you polled knowledgeable baseball fans they wouldn’t guess that Bob Lemon’s
teammates had a higher W% then Whitey Ford’s. I certainly wouldn’t have guessed it. Ned Garver is included here not because he was a great pitcher, but because his teammates were so awful that it is worth quantifying.

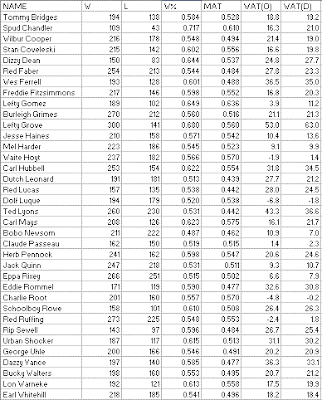
NW-NL with Wood/Patriot WAT and WCR:



We lose a second 300 game winner, as Gus Wynn drops eleven neutral wins to 289. Robin Roberts inches six games closer to the magic threshold, but is still eight short. Dizzy Trout gets the dishonor of being the first pitcher with a sub-.500 NW% that I figured. You may wonder why I included him despite an unimpressive raw record of 170-161. Well, he ranks fairly well in runs allowed based methodology. As of Total Baseball VI, circa 1998, he had an ERA+ of 124, tied for fortieth all-time, and a TPI of 34.5, good for twenty-sixth place. Again, don’t let these (NW%, WAT, etc.) figures influence your opinions of pitchers’ historical standing too much. I myself would put a lot more weight on the run-based methods then on comparisons of win-loss record.

Career WAT Data, 1920-1945

NOTE: For some reason the charts don't look as nice this time and are tough to read. If you can't read them, click on them and they will come up in full size.

Again, we’ll begin with actual W-L record and percentage, along with Mate and WAT as figured by Oliver and Deane:



Here we have the first pitchers we have encountered who were worse then their teammates, two of them Hall of Famers: Waite Hoyt and Red Ruffing, along with Dolf Luque and Charlie Root. The reason that you can be worse then your teammates and still have a positive WAT figure according to Deane’s methodology is that the method is non-linear, and considering each season separately as I have here produces a different result then figuring the career as a whole. Both Ruffing and Hoyt would have negative WAT(D) if figured for the career as a whole.

Hoyt is an interesting case for other reasons; before doing this study, I had read that Ruffing was the only Hall of Famer with a worse record then his teammates. That is true, if you figure it as most people do. Waite Hoyt’s teams, when he did not pitch, were 2004-1654, for a .548 W%, while Hoyt was 237-166 for a .566 W%. But what I do is weight each season’s Mate by the percentage of career decisions the pitcher earned that year.

I think it is obvious that this is the logically correct way to do it, but I’ll do an example just to illustrate. Suppose there was a pitcher who went 10-10 on a 86-76 team one season, and 1-0 on a 70-92 team the next. His teammates without him would be 86 + 70 -10 - 1 = 145 and 76 + 92 - 10 = 158, for a .479 W%, while our pitcher is 11-10 for a .524.

But what sense does it make to treat equally a season in which he recorded 20 decisions with one in which he recorded 1? Absolutely none. So I would say that his career Mate is 20/21*(86/162) + 1/21*(70/162) = .526. And so this pitcher is actually worse then his teammates.

In the first edition of the Historical Baseball Abstract, Bill James figured WAT by the Oliver method for a number of pitchers, and listed Career Mate as well. I don’t know why our figures diverge in many cases, but they do. For instance, he lists Hoyt’s Mate as .587, while I say it is .570 by my method and .548 by the incorrect method. Perhaps he was weighting by games or innings or something, I don’t know. Or it could be a data entry error on my end. Anyway, we do agree for a number of pitchers, so I think he was using a logical process, but I’d like to find the cause of this divergence. Anyway, it does appear that he did think about this problem the same way I did, and came to the same (IMO common sense) conclusion.

And the Wood/Patriot methodology results:



Here we lose our first 300 game winner, with Lefty Grove dropping out of the club, while still towering over his contemporaries and putting up the best NW% we’ve yet encountered. As a matter of fact, Grove has the highest NW% for any retired pitcher I’ve checked (limiting it to pitchers with 150 neutral wins--Spud Chandler’s .662 in just 152 decisions is higher), but is currently behind three active major league pitchers--it remains to be seen whether they can maintain their standing as they age (I will save their identities for a later installment, but I would think that you figure out for yourself who they are, or at least list a small group of current pitchers that they must be drawn from).

Dolf Luque skates on thin ice, narrowly avoiding the dishonor of being the first sub-.500 NW% pitcher I included in my list.

Career WAT Data, 1900-1919

See the intro to this series for a fuller explanation of the terminology and purpose of this data.

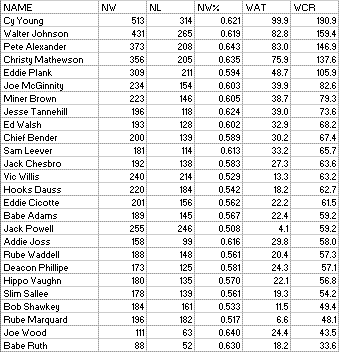
First, here are the actual W-L records of each pitcher, along with Mate, and Wins Above Team as figured by the Oliver and Deane approaches:




Career Mate is figured by weighting each year’s Mate by the percentage of lifetime decisions the pitcher earned in that year. You can see that very few of these pitchers were with bad teams on balance.

A little note on figuring these for a career. Since Oliver and Wood are strictly linear formulas, the result of figuring WAT or WCR is the same if one looks at each year separately and sums them up, or if the Career W% is compared to Career Mate. However, for Deane, the result will not be the same because a different formula is used depending on whether or not W% > Mate. I have figured career NW% for Deane by comparing to Career Mate, but have figured career Deane WAT by summing each year, because I believe this is how Total Baseball does it, and I want to match the published figures. However, my figures do not match TB in all cases, which is likely the result of data entry error on my part, although I certainly tried to be careful and have corrected any errors that I have caught. You can decide whose figures you want to go by.

Now Neutral Wins and Losses, NW%, WAT, and WCR under the Wood assumptions (list is sorted by WCR). Neutral Wins and Losses assume that the pitcher has the same number of decisions as he actually did, but wins them at his NW% instead of his actual W%:



I don’t want to get too carried away with discussion of larger truths based on these figures, as they are just a very minor part if any of how I would go about a full evaluation of pitchers, but a few points. Rube Marquard’s W-L record is not particularly impressive for a pitcher of this class. But in the Neutral measures, you can really see that he stands out as sub-par. He is over nine wins v. replacement behind the nearest HOF pitcher (Waddell), and nearly seven wins v. average behind the nearest HOF pitcher (Willis). His NW%, just like his regular W%, is the lowest here among the Hall of Famers. Addie Joss is a guy who ranks ahead of six pitchers in WAT whom he trails in WCR, fitting his short but brilliant career. We don’t kick any of the 300 game winners out of the club, and we don’t add any new members. Mathewson and Plank lose ground for pitching on good teams, while Young and Alexander barely move as they pitched on average teams, and Walter Johnson does well as he pitched for poor teams.

However, the Big Train loses almost seven wins above team versus the Deane approach, as I move the team towards .500 a lot more then Deane does. The traditional methods overstate the effect, be it giving too much credit for those on bad teams or not enough for those on good teams. Miner Brown takes a big hit here, but the Cubs teams he pitched for were probably not very well balanced between offense and defense. I believe he would do better if we adjusted based solely on the quality of offense, and he would also do better in a run/earned run/estimated run evaluation.

Babe Ruth and Joe Wood don’t really meet my criteria for this project, but I was curious about them so they are here. BTW, Wood’s ridiculous 34-5 season in 1912 comes out here as 31-8, good for +16.3 WCR, topped by only a handful of seasons in this period (including Chesbro in 1904, +19.8; Johnson in 1913, +19.5; Walsh in 1908, +18.7; Mathewson in 1908, +16.5; and matched by Cy Young in 1901).

Jack Powell is here as an interesting case, a pitcher with a .489 W% on .462 teams. I didn’t list NW% under the Oliver and Deane assumptions, but Oliver would convert that to .527, while my approach is much more conservative and puts him at .508. You will see that the more conservative approach, in many cases, is not that far removed from a pitcher’s actual record.

I don’t consider this a surprise. If you think about, when a pitcher is in the game, he is basically half of the team (again, at least while he is actually pitching and not relieved). Even if you pitch with a bunch of stiffs for offensive teammates, you have a great deal of control over whether you win or lose. Likewise, even if you pitch for a good offense, you have to hold up your end of the bargain to put up a good record.

Hall of Fame and Steroids

This is a lightweight post, borrowing heavily from other people's ideas, but the hubub about Mark McGwire and the recent Hall of Fame election really does not interest me. The Hall of Fame, or at least who is inducted in the Hall of Fame, really does not matter to me either.

Now don't get me wrong; I like to amuse myself just like many other baseball fans by raitng the players, making lists of the top 10 this or that, setting your all-time Indians starting lineup, and other such pursuits. In fact, sometime in the not too distant future I'm going to pick my top fifty starting pitchers of all-time, just for the heck of it. And I am interested in the question of who SHOULD be in the HOF. The problem is that does not so much apply to the worthy candidates of today like a Bert Blyleven as much as it does to a Rube Marquard, who is in the HOF but should not be.

Bill James once wrote something to the effect of "The Hall of Fame has lost the ability to honor a truly great player, they can only dishonor him." And this is the reason why I am disinterested. If Rube Marquard is a Hall of Famer, then what honor is there in allowing Bert Blyleven to be in the same honored company as Rube Marquard? They can only dishonor him by temporarily pretending that he does not belong.

Of course, if it was just Rube Marquard, this would not be a problem. But the Hall of Fame has so many mistakes that it is beyond salvaging. And so the tribulations of the real HOF matter little to me. That said, since the steroids debate has been rekindled, I thought I would link to this nice piece by Russ Roberts at one of my favorite non-baseball blogs, Cafe Hayek, on the issue of Big Mac and steroids and "cheating". He makes some points that I whole-heartedly agree with, and he's much smarter then I am, so he makes them eloquently and ties in Fredrich Hayek.

Career WAT Data, Intro

This post is the introduction to a series I will be doing that presents Wins Above Team statistics for each primarily twentieth century Hall of Fame pitcher (except those who were primarily relievers, so Eck is here but Sutter, Fingers, etc. are not) and some other assorted pitchers that I have chosen. Some of these pitchers were chosen by me for idiosyncratic reasons--it should not be construed as an attempt to identify the top 100 pitchers or something, just those that I was interested enough in running the numbers for. It will be broken down into historical periods roughly corresponding to those that are used to divide the history of baseball post-1900 up in the Neft & Cohen Sports Encyclopedia: Baseball. In the modern era (as divided by Neft & Cohen, 1973 to the present), I have split it up into earlier and more recent pitchers, but rather arbitrarily as you will see later. For example, Dave Stieb is a “recent” pitcher in that period and Nolan Ryan an “early” one, despite the fact that both of their careers essentially ended in 1993. I didn’t try to divide them precisely into groups, and really, the only reason I have divided them into groups is so that there is a workable number in each installment.

I am doing this not because I feel that Wins Above Team is a particularly important statistic--I would definitely consider measures based on runs or earned runs allowed, or even estimated runs allowed, to be the primary way that the value of pitchers of today and the past should be assessed. However, won-loss records can be a decent measure, if they are interpreted properly, and might possibly be able to provide some insight. Plus, W-L records will always be a primary part of the discussion by non-sabermetricians when evaluating pitchers, so we may as well be able to utilize them in the most sabermetrically sound way.

I believe that the figures that are often published, either based on comparing a pitcher to his teammate’s W-L record with his decisions removed, or Bill Deane’s modification that is used in Total Baseball, are not the most logically sound way to evaluate W-L record. I discussed this in a three part series, and will not rehash those posts here, except to give a brief explanation of the method I prefer.

Simply comparing a pitcher’s W% to that of his teammates, which I’ll call Mate as Rob Wood does, implicitly assumes that his team’s deviation from .500 is solely the product of pitching. After all, if a staff had Greg Maddux, John Smoltz, Tom Glavine, and Denny Neagle, what shame would it be if the fifth starter had a worse record then Mate, which would largely be composed of the records of the four aces? The point of considering his team’s record when evaluating a pitcher’s won-loss record is to account for the support that he received. Having Denny Neagle on the staff does not make it any easier for the #5 starter to win a game, so why compare to him?

Now of course when the standard of comparison is Mate, we cannot completely remove the influence of other pitchers, because we do not know how much of the Mate’s deviation from .500 is due to pitching or offense or any other facet of the game, without additional data, which would defeat the purpose. But we can make an assumption that will be most accurate in more situations then any other.

And that is to assume that the deviation of Mate from .500 is equally a result of offensive and defensive (or, to keep it simple, pitching) efforts. Obviously, this will not be true in all or even most cases, and sometimes will be more incorrect then assuming that the deviation is solely a product of offense, but it will have a lower average degree of error then any other assumption.

For an example of this in action, let’s look at the case of Iron Joe McGinnity, pitching for the 1905 New York Giants. His record was 21-15(.583), fairly impressive on its face, but his teammates were 84-33(.718) without him. McGinnity recorded just 24% of the team’s decisions, but 32% of its losses.

The traditional Wins Above Team method will look at the direct comparison between .718 and .583, extrapolate it over McGinnity’s 36 decisions, and proclaim that he was 4.8 wins worse then an average pitcher would have been. Bill Deane’s modified method would account for the fact that it is hard to improve on a .718 mark, with just .282 potential wins to improve, and instead estimate that McGinnity was -3.4 wins.

My method, which is essentially the same as those that have been proposed by Rob Wood and Tango Tiger (with Wood being the formative influence in my thinking on this matter), will assume that the .218 extra wins/game compared to average are half the result of offense and half of pitching, and will therefore credit .109 wins to the offense. Therefore, an average pitcher coupled with this offense would record a .609 W%. Comparing McGinnity’s .583 to this lower standard, we conclude that he was only .9 wins worse then an average pitcher.

Continuing along the same logic, I can also compare to a replacement level pitcher (the standard Oliver and Deane approaches can do this as well, although their creators did not go down this path). I assume that a replacement level pitcher is a .390 pitcher on a .500 team, and conclude that he would be a .499 pitcher with this Giants team. Comparing McGinnity’s .583 to the .499 replacement, we conclude that he was 3 wins better then replacement.

The formulas for the Wood-inspired methods are:
NW% = W% - Mate/2 + .25
WAT = (NW% - .5)*(W+L)
WCR = (NW% - .35)*(W+L)
NW = NW%*(W+L)
NL = W + L - NW

Where NW% is Neutral W%, the W% we would expect for this pitcher on a .500 team; WAT is Wins Above Team, the number of wins over what a .500 pitcher on a .500 team would have won with this team; and WCR is Wins Compared to Replacement, the number of wins above and beyond those of a hypothetical replacement level pitcher, who is assumed to be a .390 pitcher on a .500 team. NW and NL are Neutral Wins and Neutral Losses; these are the win/loss totals a pitcher would have had if he recorded the same number of decisions that he actually did, but won them at his Neutral W% rather then his actual percentage.

Next time, I will begin with a look at pitchers primarily active in the 1900-1919 period.

Hitting by Position, 2006

This is another “recycled” piece from last year, and I will not go in as much detail this time, but I do find this stuff interesting if not particularly enlightening. As with the leadoff piece, data comes from STATS, via the Baseball Direct Scoreboard.

My opinion on one-year positional hitting data being used in any sort of analysis is similar to my view on one-year park factors: not a good idea. So these figures are presented for a look at what happened in 2006, not as harbingers of future trends or anything of the sort. The positional adjustments I use when calculating runs versus a hitter at a given position are based on a ten-year sample from 1992-2001. Ideally, I should update this for the five new years of data that we have since 2001, and someday I will get around to that. But I don’t believe that those are sufficiently flawed for today’s game, and I certainly place a lot more trust in ten year figures outdated by five years then I do in one year figures.

Here are the BA/OBA/SLG and RG for each position in 2006:
C: 269/323/421/4.65
1B: 285/359/488/6.07
2B: 276/330/409/4.63
3B: 276/344/458/5.43
SS: 277/330/410/4.65
LF: 278/350/464/5.62
CF: 269/329/427/4.82
RF: 277/342/460/5.43
DH: 263/345/463/5.52
P: 131/164/175/.18

Left field was finally able to outhit right field by a significant margin, while catcher, short, and second converged to the bottom together. Pitchers still can’t hit (take note Neanderthals). The top walk rate belonged to the DHs, while first baseman led in Isolated Power but just slightly over their DH cousins, allowing the DHs to better them .325 to .318 in Secondary Average. Pitchers, dynamic and exciting element of the offensive game that they are, hit for a .083 SEC.

I always like to consider 1B and DH a group, as well as corner outfielders:
1B&DH: 278/354/480/5.89
LF&RF: 277/346/462/5.52

Here is how the positions stack up as a percentage of the overall RG, with the 1992-2001 figure in parentheses:
C: 93 (89)
1B&DH: 118 (119)
2B: 93 (93)
3B: 109 (101)
SS: 93 (86)
LF&RF: 111 (112)
CF: 97 (102)

I would give you lists of the teams with the best and worst hitting and each position, but that would insult your intelligence. It would be very similar to a list of the best individual hitters at each position. Shockingly, Phillies first baseman hit pretty well, and so did Mets centerfielders. Don’t have a clue as to why.

For pitchers, though, the best production came from St. Louis, where they scorched the ball to the tune of 173/219/222. Of course I am throwing out the AL pitchers, didn’t get many chances and were often (relatively) very good or very bad in the limited samples. The worst was Milwaukee, 097/114/113. But Texas and Oakland hurlers deserve mention for going a combined 0-32 with no walks, the only AL teams to not get a baserunner from their pitchers, let alone a hit).

It is dangerous to use the ERP formula at extremely low levels of offense like pitchers, because negative runs become unavoidable, but compared to the pitcher average of .18 RG, the Cards were +16 runs and the Brewers -18. So that’s a 3 1/2 game swing in the standings of the NL Central based on pitcher’s offense, and of course that is the largest gap in the game.

The fun part of this article a year ago was when I took the correlation, for each team, between the ten-year PADJ and the actual RG they got out of each position. Last year, only the Indians and Orioles had a negative correlation, meaning that they got better hitting out of the positions that usually are poor. In the Indians’ 2005 case, they got great production at shortstop, catcher, and center field, but horrible production at the corner positions. Here’s how it turned out in 2006 (DHs are only considered here for AL teams, pitchers not at all):
HOU…+.91
WAS…+.85
COL…+.81
BOS…+.75
CHA…+.75
STL…+.73
KC……+.68
CIN…+.66
TOR…+.66
TB……+.65
PHI…+.60
MIL…+.56
CLE…+.53
PIT…+.53
OAK…+.50
CHN…+.47
ARI…+.44
SEA…+.40
All players…+.40
LA…+.33
LAA…+.32
SD……+.27
NYN…+.21
SF……+.19
MIN…+.15
FLA…+.11
TEX……0
ATL…-.16
BAL…-.27
DET…-.29
NYA…-.34

So four team had negative correlations, with Baltimore as a repeater. You can see that the correlations are not clearly correlated with team offense as the Yankees got an unusual positional distribution of offense but still had the best offense in the league. In Baltimore’s case though, it is frustrating when you get a lot of production out of shortstop (Tejada), and then are punchless at the right side of the defensive spectrum positions like first (Conine/Millar) and DH (Gibbons/Lopez).

I will chart three teams here, Houston with the strongest correlation (and most positive), Texas with no correlation whatsoever, and New York with the strongest negative correlation. What I have done is list the positional adjustments as a baseline, then expressed each position’s RG as a percentage of the composite team RG for the positions considered. Houston, for example, got a composite 4.95 RG out of the positions considered (C, 1B, 2B, 3B, SS, LF, CF, and RF, plus DH for AL clubs). Their first baseman had a 7.94 RG, so 7.94/4.95 = 1.61:
Houston
POS……PADJ……ARG
C……… 89…………62
1B………119………161
2B………93…………83
3B………101………114
SS………86…………69
LF………112………107
CF………102………84
RF………112………127
As you can see, ever position trended in the same direction as the PADJ (by this I mean either above or below average), except for CF. In fact, most of the positions are more extreme then PADJ would guess.

Then you have the strongest negative correlation, from the Yankees:
New York(A)
POS……..PADJ……..ARG
C………89…………92
1B………119………91
2B………93…………95
3B………101………119
SS………86……… 119
LF………112……… 90
CF………102……… 93
RF………112……… 97
DH………119………104
The Yankees top hitting position was shortstop, which is generally the weakest position. Their first baseman were poor, and other positions are pretty well clustered around 100. You can see that their offensive contributions by position were much more balanced then Houston’s.

Finally, the Rangers, for whom there is no correlation either way:
Texas
POS……PADJ………ARG
C……… 89………… 88
1B………119…………122
2B………93………… 109
3B………101…………99
SS………86………… 103
LF………112…………105
CF………102…………105
RF………112…………87
DH………119…………81
Here, many of the positions match expectations, but the RFs and DHs were well below what you would expect while shortstop was well above, and it adds up to very little correlation when considered as a whole.

Leadoff Hitters, 2006

Last year I did a piece ranking the leadoff performances of each teams in a number of categories. I will do the same this year, although without a lot of the comments about each method and how it is calculated. I’ll refer you to last year’s post for that.

In brief, though, I don’t believe that this is a particularly useful activity--for the large part, hitters are hitters, regardless of what slot in the order they bat. Leadoff is probably the most important role, but in general, the best leadoff hitter and the best hitter period would be the same guy. That does not of course mean that leadoff is necessarily the best possible slot for the best hitter, but in general, too much is made of lineup construction among traditional folks anyway. Nevertheless, it is an interesting exercise if not particularly enlightening.

The data comes from the Baseball Direct Scoreboard and is for the team’s #1 slot hitters as a whole. I have listed in parentheses the guys who had the most games played while batting in the #1 spot, which sometimes is less then half of the team’s games. The “ML average” listed in the table is for ML leadoff hitters, not the entire league as a whole. I’ll sometimes discuss the league total in my comments.

The first category I’ll look at is good old runs scored, per 25.5 outs:
1. CLE(Sizemore), 7.3
2. NYA(Damon), 6.7
3. NYN(Reyes), 6.6
ML Average, 5.5
28. ARI(Counsell), 4.8
29. CIN(Freel), 4.6
30. CHN(Pierre), 4.2
Johnny Damon’s Red Sox were number one a year ago, and his Yankees are #2 this go around. Of course, runs scored are heavily influenced by the succeeding batters, and it’s little surprise three of the game’s best offenses are represented in the top 3 spots here. Juan Pierre was seen as a leadoff solution for the Cubs, but as I pointed out last year, this was dubious as he was coming off a year in Florida in which the Marlins were in many of the trailer categories.

On Base Average is an obvious criteria to look at:
1. CLE(Sizemore), .369
2. LA(Furcal), .366
3. SEA(Suzuki), .365
ML Average, .339
28. ARI(Counsell), .301
29. MIL(Weeks), .300
30. PIT(Duffy), .298
The average for all players was .333, so the leadoff advantage is only six points; last year it was ten. The Yankees are fourth on the list, so Damon did his job, although none of the OBAs are eye-popping for an individual player.

Runners On Base Average removes HR and CS from OBA, leaving it not as a pure measure of skill but as an accounting for the percentage of PA in which the leadoff men sets the table by remaining on base:
1. SEA(Suzuki), .351
2. LA(Furcal), .330
3. OAK(Kendall), .327
ML Average, .305
28. WAS(Soriano), .271
29. ARI(Counsell), .267
30. MIL(Weeks), .265
The average for all hitters was .293, making a larger leadoff/overall gap in ROBA then in OBA. Last year, when the opposite was true, I presumed it was because of the high number of caught stealings racked up by leadoff hitters. Washington is near the bottom here because of Soriano’s 40 HR season (they ranked ninth in OBA). The usual suspects, Cleveland and New York, come in at seventh (.321) and eleventh (.318) respectively.

Run Element Ratio from Bill James is not a skill or production measure at all. It is a ratio between offensive elements ideally placed at the beginning of an inning to set it up (walks and steals) versus those ideally placed at the end to clean it up (extra bases):
1. LAA(Figgins), 2.1
2. OAK(Kendall), 1.8
3. MIN(Castillo), 1.7
ML Average, 1.0
28. CLE(Sizemore), .6
29. TOR(Johnson), .6
30. TEX(Matthews), .6
The overall average is .7, and only five teams were below that with their leadoff hitters (the three above as well as Kansas City and Tampa Bay). Sizemore’s power again put Cleveland in the bottom three, while Texas is last for the second year in a row despite changing their primary leadoff hitter from David Dellucci to Gary Matthews. Since those two are now in Cleveland and Los Angeles, we’ll see if they can do it again with a new man in 2007.

Another Bill James tool was his own method for evaluating leadoff hitters, which I call Leadoff Efficiency. This is the number of expected runs scored per 25.5 outs, which is a (relatively) pure of the leadoff man, unlike the actual runs scored figures we looked at first:
1. CLE(Sizemore), 7.1
2. NYN(Reyes), 6.6
3. WAS(Soriano), 6.6
ML Average, 5.6
28. STL(Eckstein), 4.8
29. ARI(Counsell), 4.7
30. MIL(Weeks), 4.6
Damon is again just off the list, fourth at 6.5. Last year the leadoff efficiency formula overestimated actual runs scored for leadoff hitters by a fairly big margin, but this year, the actual was 5.49 and the expected 5.55, not bad at all. Scott Podsednik is fourth to last and Chone Figgins sixth to last.

One can always just look at a leadoff hitter just like we would any other. So here is the list by good old Runs Created per Game:
1. CLE(Sizemore), 6.9
2. NYN(Reyes), 6.4
3. WAS(Soriano), 6.3
ML Average, 4.9
28. LAA(Figgins), 3.9
29. ARI(Counsell), 3.9
30. MIL(Weeks), 3.7
The average for all hitters was 5.0, so once again the average leadoff hitter was worse then the average hitter. Damon is fourth at 6.2

Last year I included what I called Pure Leadoff RAA. Basically, it is the linear weight RAA total a player would get if he always batted with nobody on base and nobody out (the ideal leadoff situation). I based it off of Pete Palmer’s Run Expectancy table from The Hidden Game for simplicity’s sake, which means it is not fully adapted to the run environment of today’s game, but the values should not be too far off. One assumption that the formula makes that I did not mention last year is it assumes that all stolen base attempts occur during the next batter’s PA (or in other words, in a runner at first, no out situation). Here are the figures in this category:
1. CLE(Sizemore), +37
2. NYN(Reyes), +32
3. WAS(Soriano), +29
ML Average, +1
28. ARI(Counsell), -9
29. STL(Eckstein), -10
30. MIL(Weeks), -12
NYA is again fourth at +27. The top three are the same as the RG list for overall hitting, with Soriano’s homers only worth 1 run instead of 1.46 there.

Last year, David Smyth suggested that I look at a modified OPS, 2*OBA + SLG, which I will call 2OPS. Since the optimal OPS construction is something like 1.7 or 1.8*OBA + SLG, using 2 is a way to give a bit more credit to the on base side of things while still having a decent overall measure of production. Since the OPS units are meaningless anyway, I scaled these back so that the league 2OPS ~ league OPS. So these figures are for (2*OBA + SLG)*.7:
1. CLE(Sizemore), 893
2. WAS(Soriano), 864
3. TEX(Matthews), 847
ML Average, 767
28. ARI(Counsell), 686
29. PIT(Duffy), 680
30. MIL(Weeks), 677

Although he may not fit the ideal prototype of a leadoff hitter, Grady Sizemore still comes out on top in most categories as the top leadoff hitter in the game in 2006, with Jose Reyes, Alfonso Soriano, and Johnny Damon close behind in many categories.

Historical Hitting by Postion

I’m excessively fond of chiding the National League as the “Neanderthal League” at every available opportunity for their refusal to use the designated hitter. I don’t wish to discuss the DH here per se, but use one argument against it that you’ll occasionally see as a springboard for discussion.

Sometimes the anti-DH argument will include the rhetorical question, “Why stop at pitcher? Why not have a defensive shortstop and a DH for him, or a defensive catcher and a DH for him.” While it is true of course that you could put together a better offense by completely ignoring defensive ability, there is absolutely no comparison between the performance of shortstops relative to the population of hitters at large and that of pitchers. In order to believe that the circumstances would become such that there would be popular support for a similar shortstop or catcher DH, one must assume I would think that shortstops, like pitchers, have progressively seen their offensive levels decline relative to hitters as a whole.

And this is a useful point for a brief discussion of offensive positional adjustments throughout the decades. While this question is just one part of a tangled web of questions dealing with how to value players at different positions, I’m not going to discuss that issue but just the historical facts.

On my website, there is a chart showing offensive PADJs broken down by into the ten decades from 1900-1998. There are a couple issues with this chart; first, it considers a player only at the position he is listed at first in Total Baseball. In other words, the position in which he played the most games in a given season is his position. If a player appeared in 25 games as an outfielder and 24 as a first baseman, he is 100% an outfielder. Secondly, it does not account for the three outfield positions, but lumps them altogether. And thirdly, it uses the flawed model of basic Runs Created to evaluate each player’s offense.

With the exception of problem two, in which we lose valuable data on the breakdown between outfield positions, I don’t believe that the other two flaws are particularly consequential when dealing with a large group of aggregated players.

Looking at the chart, one of the most interesting things is that third baseman were worse hitters then second baseman in the 1900-1929 period. It is not until the thirties that third baseman hit better then second baseman. This phenomenon has been noted by other analysts, notably Bill James in Win Shares; I’m just pointing out that this data agrees with the earlier conclusions (which of course it should since the other studies were constructed similarly).

Getting to the issue of offensive balance between the positions and whether or not it has declined historically, if you look at the field non-pitching fielding positions (here catcher, first, second, third, short, and outfield), you will see that the standard deviation of position adjustment was higher in the early days then it is today:
1900: .154, 1910: .143, 1920: .156, 1930: .156, 1940: .132, 1950: .122, 1960: .151, 1970: .159, 1980: .134, 1990: .135, 1900-1998: .134

“1900” means the ten-year period starting in 1900 (1900-1909), and so on. In fact, the highest standard deviation came in the 1970s when the DH was adopted. In the 70s, shortstops hit at just 77% of the league average (only aught catchers hit worse, 76%). But this is still a far cry from pitchers’ best showing, 45% in the aughts and the twenties. Pitchers showed a pattern of steady decline to as low as 30% in the 60s and 70s when the DH came of age and 26% and 27% in the eighties and nineties.

The best offensive showing by any position is the first sackers of the 1930s, 129%. In an eight team universe, Lou Gehrig, Jimmie Foxx, and later Hank Greenberg and Johnny Mize are bound to wreck some havoc on the overall figures.

Anyway, you can pursue the chart yourself if you wish for other interesting things. The main point I wanted to make is that at no time in twentieth century major league history has the balance of offensive production between the positions been greater then in the 1980s and 1990s. While the chart does not include 1999-2006, I do not believe that the trend would be significantly different.

It is possible I suppose that the DH itself has had some impact on this. DHs would probably be stuck at 1B or a corner outfield perch in earlier times, and allowing them their own category would allow defensive specialists to sneak in the field at those positions while maintaining overall offensive output. This could cause the balance between the fielding positions to be greater then it would be in absence of the DH. First base offense has been essentially unchanged since the 70s, but outfielders have dropped a little bit. But even if this effect is significant, I don’t believe that it is significant enough to mask a markedly worsening balance or collapse of short, catcher, or other low-offense positions. In fact, shortstops have bounced back relative to the league hitting as a whole form the aforementioned 77% in the 70s; the composite league comparison compares to all hitters, including DHs.

I don’t think that the historical data shows a significant trend, taking a full century view, towards more or less of a balance. But it clearly does not show the widening balance that would justify concerns about multiple DHs becoming a possibility. And if you think that I’ve wasted your time with some rudimentary stuff and this whole thing was an excuse to get a post up finally and bash the NL some more, you might be on to something.